Абсолютная величина числа
Определение. Абсолютной величиной (или модулем) действительного числа  (обозначается (обозначается  ) называется неотрицательное число, удовлетворяющее условиям: ) называется неотрицательное число, удовлетворяющее условиям:
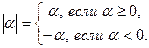
Ясно, что всегда
 . (3.1) . (3.1)
Свойства абсолютных величин:
1)  ; 2) ; 2)  ; 3) ; 3) 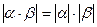 ; 4) ; 4)  . .
Доказательство. 1) Если  , то , то  в силу (3.1). Если в силу (3.1). Если  , то , то 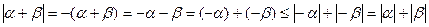 . Первое свойство доказано. . Первое свойство доказано.
2) Имеем  , отсюда , отсюда  . Второе свойство доказано. . Второе свойство доказано.
3)  , третье свойство доказано. , третье свойство доказано.
Четвертое свойство доказывается так же, как свойство 3).
Замечание. Свойство 1) распространяется на любое число слагаемых, свойство 3) – на любое число сомножителей.
Отметим также, что   , т.е. х удовлетворяет неравенству , т.е. х удовлетворяет неравенству 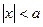 тогда и только тогда, когда принадлежит интервалу тогда и только тогда, когда принадлежит интервалу 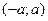 . .
Геометрический смысл модуля действительного числа состоит в том, что  равен расстоянию от точки х на числовой прямой до нуля. равен расстоянию от точки х на числовой прямой до нуля.
Дата добавления: 2015-01-18 | Просмотры: 927 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
