 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Глава 1. Введение в математический анализК дисциплинарной ответственности работники привлекаются за совершение дисциплинарного проступка. Дисциплинарным проступком признается противоправное виновное невыполнение или ненадлежащее исполнение работником своих трудовых обязанностей, а также нарушение правил внутреннего распорядка. Привлечение работника к дисциплинарной ответственности – это право, а не обязанность работодателя. Целью привлечения к дисциплинарной ответственности является не только наказание виновного, но и воспитание других работников. За совершение дисциплинарного проступка работодатель имеет право применить следующие дисциплинарные взыскания: замечание, выговор, увольнение по соответствующим основаниям.
Условия привлечения к дисциплинарной ответственности: • вред, причиненного трудовой дисциплине; • противоправность; • вина; • причинно-следственная связь между противоправным поведением и вредом, причиненным трудовой дисциплине. Причиненный вред не всегда может быть выражен в наличии материального ущерба. Вред причиняется самому порядку в организации, то есть трудовой дисциплине, и заключается в возникновении негативной мотивации у других работников. Противоправность заключается в том, что работник в результате своего действия или бездействия не выполнил трудовые обязанности или нарушил правила внутреннего трудового распорядка. В приказе о привлечении к дисциплинарной ответственности следует указать, в чем конкретно выражена противоправность, то есть какие нормы права были нарушены. Незнание работника своих должностных обязанностей не освобождает его от ответственности. Если должностная инструкция работника изменяется в период его работы, то с этими изменениями он должен быть ознакомлен под роспись.
Основанием для освобождения от дисциплинарной ответственности является: 1. действие непреодолимой силы - например, работник опоздал на работу вследствие наличия больших снежных заносов на дороге, наводнения и т. д.; 2. наличие крайней необходимости или необходимой обороны (например, работник не явился на работу вследствие того, что оказывал помощь в тушении пожара); 3. отсутствие одного из условий привлечения к дисциплинарной ответственности, например, противоправности (например, работника нельзя привлечь к дисциплинарной ответственности за невыполнение обязанности, не предусмотренной его трудовым договором). 4. неисполнение работодателем обязанностей по созданию работникам надлежащих условий труда. Трудовым кодексом предусмотрен строгий порядок наложения дисциплинарного взыскания: а) срок наложения взыскания, б) наличие письменного объяснения, в) приказ о применении дисциплинарного взыскания. Дисциплинарное взыскание применяется не позднее одного месяца со дня обнаружения проступка, не считая времени болезни работника, пребывания его в отпуске, а также времени, необходимого на учет мнения представительного органа работников. Дисциплинарное взыскание не может быть применено позднее шести месяцев со дня совершения проступка, а по результатам ревизии, проверки финансово-хозяйственной деятельности или аудиторской проверки – позднее двух лет со дня его совершения. В указанные сроки не включается время производства по уголовному делу. За каждый дисциплинарный проступок может быть применено только одно дисциплинарное взыскание. Днем обнаружения проступка является день, когда непосредственный руководитель узнал (должен был узнать) о его совершении. Работодатель обязан взять у работника письменное объяснение по факту дисциплинарного нарушения. Однако давать объяснения – это право, но не обязанность работника. Если работник отказывается давать объяснения, то в присутствии его и двух свидетелей составляется акт об отказе давать письменные объяснения. Отказ работника дать объяснения не является препятствием для применения дисциплинарного взыскания. Приказ (распоряжение) или постановление о применении дисциплинарного взыскания с обязательным указанием мотивов его применения объявляется работнику под расписку в течение трех рабочих дней со дня его издания. В случае отказа от подписи приказом оформляется соответствующий акт. Дисциплинарное взыскание считается наложенным правомерно, если были соблюдены все условия привлечения к ответственности и процедура привлечения к ответственности. По общему правилу дисциплинарное взыскание действует в течение 12 месяцев с момента его наложения. Если работник совершил новый дисциплинарный проступок и был привлечен к дисциплинарной ответственности, то срок действия первого взыскания продлевается до окончания срока второго дисциплинарного взыскания. Взыскание может быть снято автоматически либо по распоряжению работодателя. Взыскание снимается автоматически при увольнении работника и при истечении срока действия взыскания. Работодатель до истечения года со дня применения дисциплинарного взыскания имеет право снять его с работника по собственной инициативе, просьбе самого работника, ходатайству его непосредственного руководителя или представительного органа работников. Дисциплинарное взыскание может быть обжаловано работником в Комиссию по трудовым спорам организации, или в суд.
Контрольные вопросы:
1. Охарактеризуйте специфику трудового правоотношения. 2. Раскройте содержание понятия и предмета трудового права. 3. Проанализируйте функции, принципы и источники трудового права. 4. Субъектный состав трудовых правоотношений. 5. Охарактеризуйте механизмы правового регулирования занятости и трудоустройства. 6. Раскройте понятие трудового права и охарактеризуйте его виды. 7. Охарактеризуйте основания прекращения трудового договора. 8. Расторжение трудового договора по инициативе работодателя. 9. Понятие рабочего времени и его виды. 10.Понятие времени отдыха и его виды. 11.Раскройте правовые механизмы исчисления оплаты труда и системы заработной платы. 12. Понятие дисциплинарного правонарушения и его состав. 13. Виды дисциплинарных санкций и порядок их наложения.
Глава 1. Введение в математический анализ
Литература 1. Фихтенгольц Г.М. Основы математического анализа, ч. I. 2. Бохан К.А., Егорова И.А., Лащенов К.В. Курс математического анализа, т. I. 3. Ильин В.А., Позняк Э.Г. Основы математического анализа, ч. I. 4. Кудрявцев Л.Д. Курс математического анализа, т. I. 5. Давыдов Н.А., Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу.
§ 1. Множество R действительных чисел и его свойства Из школьного курса математики известны множества натуральные числа N = {1;2;…; n;…}, целых чисел
Рассмотрим теорию Дедекинда (1831-1916, немецкий математик) новых чисел, которые будем называть иррациональными. Разобьем множество Q рациональных чисел на два непустых множества А и 1) каждое рациональное число в одно и только в одно из множеств А или 2) каждое число Разбиение Q, удовлетворяющее указанным двум условиям, называется сечением в множестве рациональных чисел. Множество А называется нижним классом сечения, множество Примеры. 1) Определим А как множество всех рациональных чисел а, удовлетворяющих неравенству Ясно, что таким образом получим сечение множества рациональных чисел, причем число 1 принадлежит классу 2) К нижнему классу А отнесем все рациональные числа а, удовлетворяющие неравенству Получим сечение, причем в верхнем классе нет наименьшего числа, а в нижнем классе есть наибольшее число 1. 3) Отнесем к классу А все положительные рациональные числа а, для которых Очевидно, что полученное разбиение является сечением. Докажем, что в классе А нет наибольшего числа. Пусть а – любое положительное число класса А, т.е. Неравенство Итак, какое бы положительное число Аналогично доказывается, что в классе Ясно также, что не может существовать сечение, у которого одновременно в нижнем классе есть наибольшее число Действительно, предположим, напротив, что такое сечение существует. Положим Таким образом, сечения могут быть только трех видов, иллюстрируемых примерами 1), 2), 3): 1) в нижнем классе А нет наибольшего числа, а в верхнем классе 2) в нижнем классе А есть наибольшее число r, а в верхнем классе 3) ни в нижнем классе нет наибольшего числа, ни в верхнем классе нет наименьшего числа. В первых двух случаях говорят, что сечение производится рациональным числом r (которое является пограничным между классами А и Заметим, что рациональное число r может определяться сечениями двух видов 1) и 2). Для определенности обычно считают, что рациональное число r определяет сечение, у которого r принадлежит верхнему классу Рациональные и иррациональные числа получили общее название действительных (или вещественных) чисел. Множество действительных чисел обозначают буквой R. Рассмотрим теперь некоторые свойства множества R действительных чисел. Определение 1. Два действительных числа Определение 2. Пусть Лемма 1. Для любых двух действительных чисел Доказательство. Пусть Доказанное в лемме 1 свойство множества R действительных чисел называется его упорядоченностью по величине. С помощью определения 2 легко доказать, что: 1) если 2) если Лемма 2. Каковы бы ни были два различных действительных числа Доказательство. Пусть Определение 3. Упорядоченное множество называется плотным, если между любыми его элементами лежит третий элемент этого множества. Из леммы 2 и определения 3 следует, что множество R действительных чисел – плотное. Более того, доказано, что между любыми двумя действительными числами лежит рациональное число. Это свойство множества R называется усиленной плотностью множества действительных чисел. Замечание. С помощью леммы 2 легко показать, что между любыми двумя различными действительными числами лежит бесконечно много действительных и, в частности, рациональных, чисел. Рассмотрим еще одно свойство множества R действительных чисел, которое существенно отличает его от множества Q рациональных чисел. Рассматривая сечения в множестве рациональных чисел, мы видели, что иной раз для такого сечения не находилось пограничного рационального числа, которое производит это сечение (сечение третьего вида). Именно эта неполнота множества рациональных чисел, наличие в нем этих пробелов и послужили основанием для введения новых чисел – иррациональных. Спрашивается, а как будет обстоять дело, если производить сечение множества действительных чисел? Будут ли такие же «дыры», как в случае сечения множества рациональных чисел, или нет? Для ответа на эти вопросы рассмотрим сечение множества R действительных чисел, т.е. такое разбиение R на два непустых класса 1) каждое действительное число попадает в одно и только одно из множеств 2) каждое число Имеет место Теорема Дедекинда. Для всякого сечения Доказательство. Обозначим через А множество всех рациональных чисел из множества Аналогично доказывается, что если Таким образом, из теоремы Дедекинда следует, что в случае сечения множества R действительных чисел нет «дыр», имевших место для сечения множества Q рациональных чисел. Всегда есть пограничное действительное число, производящее данное сечение множества R. Это свойство множества R действительных чисел называется его полнотой или непрерывностью.
Дата добавления: 2015-01-18 | Просмотры: 1113 | Нарушение авторских прав |
 , рациональных чисел
, рациональных чисел  . Известно также, что этих чисел недостаточно для измерения отрезков. Например, рассмотрим прямоугольный треугольник, длины катетов которого равны 1, т.е.
. Известно также, что этих чисел недостаточно для измерения отрезков. Например, рассмотрим прямоугольный треугольник, длины катетов которого равны 1, т.е.  . Тогда по теореме Пифагора
. Тогда по теореме Пифагора  . Покажем, что
. Покажем, что длина с гипотенузы не может быть рациональным числом. Предположим, напротив, что с – рациональное число, т.е.
длина с гипотенузы не может быть рациональным числом. Предположим, напротив, что с – рациональное число, т.е.  , ас причем дробь
, ас причем дробь  несократима. Тогда
несократима. Тогда  , откуда b
, откуда b 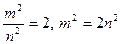 . Поскольку
. Поскольку 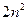 – четное число, то и
– четное число, то и  – четное число, а тогда и т – четное число, так как квадрат нечетного числа всегда число нечетное. Пусть т =2 k. Тогда
– четное число, а тогда и т – четное число, так как квадрат нечетного числа всегда число нечетное. Пусть т =2 k. Тогда 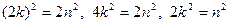 , т.е. и n – четное число и потому дробь
, т.е. и n – четное число и потому дробь 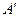 так, что:
так, что: меньше каждого числа
меньше каждого числа  .
. .
. , а к множеству
, а к множеству  , для которых
, для которых  .
. ).
).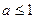 , к верхнему классу
, к верхнему классу  .
. , число нуль и все отрицательные рациональные числа, а к классу
, число нуль и все отрицательные рациональные числа, а к классу  .
. , так что и число
, так что и число  .
.
 . Последнее неравенство тем более будет выполнено, если n удовлетворяет неравенству
. Последнее неравенство тем более будет выполнено, если n удовлетворяет неравенству 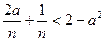 , т.е.
, т.е.  , для чего достаточно взять
, для чего достаточно взять  .
.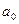 , а в верхнем классе – наименьшее число
, а в верхнем классе – наименьшее число 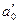 .
. . Ясно, что с – рациональное число, причем
. Ясно, что с – рациональное число, причем  . Число с не может принадлежать классу А, так как
. Число с не может принадлежать классу А, так как  . Мы как бы вставляем его между всеми числами а класса А и всеми числами
. Мы как бы вставляем его между всеми числами а класса А и всеми числами  .
. , определяемых соответственно сечениями
, определяемых соответственно сечениями  , считаются равными тогда и только тогда, когда эти сечения тождественны, т.е.
, считаются равными тогда и только тогда, когда эти сечения тождественны, т.е.  .
. , если класс А целиком содержит в себе класс В, не совпадая с ним (т.е.
, если класс А целиком содержит в себе класс В, не совпадая с ним (т.е.  ). Говорят, что
). Говорят, что  , если
, если  .
. .
. ; 2)
; 2)  3)
3)  . Из этих соотношений и определений 1 и 2 вытекает утверждение леммы. Лемма доказана.
. Из этих соотношений и определений 1 и 2 вытекает утверждение леммы. Лемма доказана.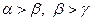 ,
,  ;
; ,
,  (доказать дома студентам самим).
(доказать дома студентам самим). . Поэтому
. Поэтому  (равенство возможно, если
(равенство возможно, если  . Лемма доказана.
. Лемма доказана. и
и 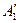 , что:
, что: меньше каждого числа
меньше каждого числа  .
. в множестве действительных чисел существует действительное число
в множестве действительных чисел существует действительное число  . Докажем, что тогда
. Докажем, что тогда 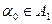 , такое, что
, такое, что  . Тогда по лемме 2 существует рациональное число r:
. Тогда по лемме 2 существует рациональное число r:  , принадлежащее
, принадлежащее