|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Обратная функция
Пусть  – некоторая функция, – некоторая функция, 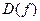 и и  - ее область определения и область значений соответственно. Если любым различным значениям аргумента соответствуют различные значения функции, то есть из - ее область определения и область значений соответственно. Если любым различным значениям аргумента соответствуют различные значения функции, то есть из  , ,    , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение 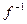 множества множества  на множество на множество 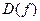 . Это отображение называется обратной функцией к функции . Это отображение называется обратной функцией к функции  , то есть обратная функция , то есть обратная функция 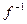 такова, что такова, что  . Функция . Функция  и обратная для нее функция и обратная для нее функция  называются взаимно-обратными функциями. Заметим, что называются взаимно-обратными функциями. Заметим, что  , а графики взаимно-обратных функций , а графики взаимно-обратных функций  и и  симметричны относительно прямой симметричны относительно прямой 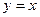 – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз. – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз.
Чтобы найти аналитическое выражение для функции 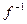 , обратной к функции , обратной к функции  , нужно решить уравнение , нужно решить уравнение  относительно х, и если при этом получается несколько значений х, то выбрать те значения, которые принадлежат относительно х, и если при этом получается несколько значений х, то выбрать те значения, которые принадлежат 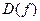 . Таким образом получают равенство . Таким образом получают равенство  , в котором обычно заменяют у на х и х на у. , в котором обычно заменяют у на х и х на у.
Обратные функции для функций  нужно рассмотреть на практических занятиях. нужно рассмотреть на практических занятиях.
функцию. Найдем ее. Имеем  т.е. т.е. 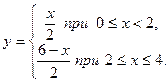 Отметим, что каждое свое Отметим, что каждое свое
| | Заметим, что условие строгой монотонности функции является достаточным, но не необходимым условием существования обратной функции. Пусть, например, 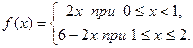 Эта функция не монотонна на Эта функция не монотонна на 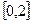 , однако имеет обратную , однако имеет обратную

значение функция  принимает только один раз (такие функции называются инъективными). принимает только один раз (такие функции называются инъективными).
Дата добавления: 2015-01-18 | Просмотры: 946 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|

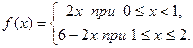 Эта функция не монотонна на
Эта функция не монотонна на 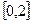 , однако имеет обратную
, однако имеет обратную
 – некоторая функция,
– некоторая функция, 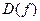 и
и  - ее область определения и область значений соответственно. Если любым различным значениям аргумента соответствуют различные значения функции, то есть из
- ее область определения и область значений соответственно. Если любым различным значениям аргумента соответствуют различные значения функции, то есть из  ,
, 

 , то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение
, то, как известно из § 8, отображение f, определяемое этой функцией, обратимо, и для него существует обратное отображение 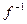 множества
множества  . Функция
. Функция  называются взаимно-обратными функциями. Заметим, что
называются взаимно-обратными функциями. Заметим, что  , а графики взаимно-обратных функций
, а графики взаимно-обратных функций 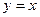 – биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз.
– биссектрисы первого и третьего координатных углов. Обратная функция всегда существует для строго монотонной функции, которая каждое свое значение принимает только один раз. , в котором обычно заменяют у на х и х на у.
, в котором обычно заменяют у на х и х на у. нужно рассмотреть на практических занятиях.
нужно рассмотреть на практических занятиях. т.е.
т.е. 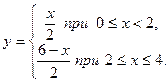 Отметим, что каждое свое
Отметим, что каждое свое

 принимает только один раз (такие функции называются инъективными).
принимает только один раз (такие функции называются инъективными).