 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Четные и нечетные функции. Периодические функции
Определение 1. Функция
Таким образом, функция может быть четной или нечетной только тогда, когда ее область определения симметрична относительно начала координат на числовой прямой (числа х и – х одновременно принадлежат Функция Функция Функция График четной функции симметричен относительно оси Оу, так как если точка При доказательстве четности или нечетности функции бывают полезны следующие утверждения. Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная). б) Произведение двух четных (нечетных) функций есть функция четная. в) Произведение четной и нечетной функций есть функция нечетная. г) Если f – четная функция на множестве Х, а функция g определена на множестве д) Если f – нечетная функция на множестве Х, а функция g определена на множестве Доказательство. Докажем, например, б) и г). б) Пусть г) Пусть f – четная функция. Тогда Остальные утверждения теоремы доказываются аналогично. Теорема доказана. Теорема 2. Любую функцию Доказательство. Функцию
Функция Определение 2. Функция
Такое число T называется периодом функции Из определения 1 следует, что если Т – период функции Определение 3. Наименьший из положительных периодов функции называется ее основным периодом. Теорема 3. Если Т – основной период функции f, то остальные периоды кратны ему. Доказательство. Предположим противное, то есть что существует период
то есть Хорошо известно, что тригонометрические функции являются периодическими. Основной период
Отсюда
Значение T, определяемое из первого равенства, не может быть периодом, так как зависит от х, т.е. является функцией от х, а не постоянным числом. Период определяется из второго равенства: Примером более сложной периодической функции является функция Дирихле
Заметим, что если T – рациональное число, то
при любом рациональном числе T. Следовательно, любое рациональное число T является периодом функции Дирихле. Ясно, что основного периода у этой функции нет, так как есть положительные рациональные числа, сколь угодно близкие к нулю (например, рациональное число Теорема 4. Если функция f задана на множестве Х и имеет период Т, а функция g задана на множестве Доказательство. Имеем
то есть утверждение теоремы доказано. Например, так как cos x имеет период Определение 4. Функции, не являющиеся периодическими, называются непериодическими.
Дата добавления: 2015-01-18 | Просмотры: 1544 | Нарушение авторских прав |
 называется четной (нечетной), если вместе с каждым значением переменной
называется четной (нечетной), если вместе с каждым значением переменной  значение – х также принадлежит
значение – х также принадлежит 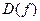 и выполняется равенство
и выполняется равенство (11.1)
(11.1)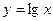 не является четной и нечетной, так как ее область определения
не является четной и нечетной, так как ее область определения 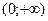 не симметрична относительно начала координат.
не симметрична относительно начала координат. четная, так как
четная, так как  симметрична относительно начала координат и
симметрична относительно начала координат и 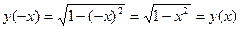 .
. нечетная, так как
нечетная, так как  и
и 
 .
. не является четной и нечетной, так как хотя
не является четной и нечетной, так как хотя  .
. принадлежит графику, то и точка
принадлежит графику, то и точка  тоже принадлежит графику. График нечетной функции симметричен относительно начала координат, так как если
тоже принадлежит графику. График нечетной функции симметричен относительно начала координат, так как если  тоже принадлежит графику.
тоже принадлежит графику.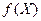 , то функция
, то функция  – четная.
– четная. и
и  – четные функции. Тогда
– четные функции. Тогда  , поэтому
, поэтому 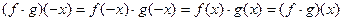 . Аналогично рассматривается случай нечетных функций
. Аналогично рассматривается случай нечетных функций  .
.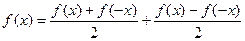 .
. – четная, так как
– четная, так как  , а функция
, а функция  – нечетная, поскольку
– нечетная, поскольку  . Таким образом,
. Таким образом,  , где
, где  – четная, а
– четная, а  , такое, что при любом
, такое, что при любом  и
и  также принадлежат области определения
также принадлежат области определения  .
. , тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов.
, тоже является периодом. Отсюда следует, что если функция имеет период, то она имеет бесконечно много периодов. функции f (
функции f ( , где
, где  . Поэтому
. Поэтому ,
, – период функции f, причем
– период функции f, причем  и
и  равен
равен  ,
,  и
и  . Найдем период функции
. Найдем период функции 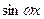 . Пусть
. Пусть  (так как
(так как  .
.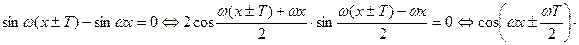
 или
или  или
или  или
или  .
. наименьший положительный период получается при
наименьший положительный период получается при  :
:  . Это – основной период функции
. Это – основной период функции 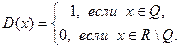
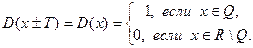
 можно сделать выбором n сколь угодно близким к нулю).
можно сделать выбором n сколь угодно близким к нулю). тоже имеет период Т.
тоже имеет период Т. , поэтому
, поэтому ,
, имеют период
имеют период