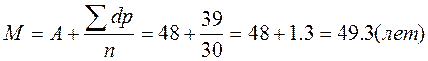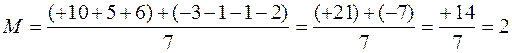|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Для сгруппированного вариационного ряда(I—обычный способ, II—способ моментов)
Средняя арифметическая имеет следующие свойства: 1. сумма отклонений от средней равна нулю (см. табл. 2, гр. 5); 2. при умножении (делении) всех вариант на один и тот же множитель (делитель) средняя арифметическая умножается (делится) на тот же множитель (делитель); 3. если прибавить (вычесть) ко всем вариантам одно и то же число, средняя арифметическая увеличивается (уменьшается) на то же число. Эти свойства могут быть использованы для облегчения и упрощения расчета средней арифметической. Первое свойство, например, служит обоснованием для расчета средней арифметической по способу моментов. Как видно из табл. 2 (гр. 5), сумма всех отклонений вариант от средней равна нулю (отклонение d — это разность между каждой вариантой и средней величиной, т. е. d = V-M). Поскольку в сгруппированном вариационном ряду варианты имеют различную частоту, то каждая из них в итоге дает отклонения, зависящие от этой повторяемости. Следовательно, значение отклонения варианты необходимо умножить на частоту, а затем суммировать все эти произведения. Каждая варианта отклоняется от средней величины в большую или меньшую сторону со знаком «+» или «-». Эти значения следует учитывать при проведении вычислений. Сумма отрицательных отклонений равна -72,9, сумма положительных отклонений составляет 72,9, а итоговая сумма всех отклонений равна нулю (Σdp = 0). Это свидетельствует о том, что средняя величина действительно есть общая количественная характеристика данного вариационного ряда, так как она взаимоисключает, взаимоуничтожает все отклонения. Это свойство положено в основу вычисления средней величины по способу моментов. Значение средней определяется по формуле
Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом. При выборе условной средней А следует ориентироваться на моду или медиану. Способ моментов значительно упрощает расчеты и делает их более быстрыми. Второе свойство средней арифметической полезно применять при анализе вариационного ряда, состоящего либо из очень больших, либо из очень малых величин. Имеются, например, варианты: 0,0001; 0,0002; 0,0003. Используя это свойство, увеличим их в 10000 раз. Получим величины 1, 2, 3. Средняя арифметическая из них равна 2, а искомая средняя арифметическая в 10000 раз меньше, т. е. 0,0002. При обработке вариационного ряда, состоящего их положительных и отрицательных значений, иногда бывает полезно прибавить ко всем вариантам такое число, чтобы сделать их все положительными. Из полученного среднего результата эту величину следует вычесть. Например, имеются величины: +10, +5, -3, -1, +6, -1, -2. Определим среднюю арифметическую:
Чтобы избавиться от отрицательных величин, можно использовать третье свойство средней арифметической, т. е. прибавить к каждой варианте определенное число, например, в нашем случае 4. Тогда величины приобретут следующий вид: 14, 9, 1, 3, 10, 3, 2. Их сумма равна 42. При делении на 7 получим 6. При вычитании 4 из 6 получим среднюю арифметическую величину 2.
Дата добавления: 2015-02-02 | Просмотры: 831 | Нарушение авторских прав |
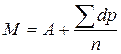 , где А является условной средней величиной. Если А является истинной средней, т. е. А = М, то сумма ее отклонений будет равна нулю, если же она не является истинной средней, то сумма отклонений будет иметь значение, отличное от нуля, и явится основой для определения поправки. В табл. 2 (II способ) показаны этапы вычисления средней величины по способу моментов (А = 48). Из гр. 9 табл. 2 видно, что сумма отклонений Σdp равна 39. С учетом поправки легко определить действительное значение средней величины, подставив соответствующие значения в формулу:
, где А является условной средней величиной. Если А является истинной средней, т. е. А = М, то сумма ее отклонений будет равна нулю, если же она не является истинной средней, то сумма отклонений будет иметь значение, отличное от нуля, и явится основой для определения поправки. В табл. 2 (II способ) показаны этапы вычисления средней величины по способу моментов (А = 48). Из гр. 9 табл. 2 видно, что сумма отклонений Σdp равна 39. С учетом поправки легко определить действительное значение средней величины, подставив соответствующие значения в формулу: