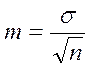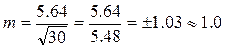АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

ОПРЕДЕЛЕНИЕ ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ

Прочитайте:
  1. A- Определение индекса гигиены полости рта
  2. E Определение в крови уровней мочевины и креатинина
  3. I. Аборты. Определение понятия.
  4. I. Иммунология. Определение, задачи, методы. История развитии иммунологии.
  5. I. Определение инфекционного процесса и формы его проявления.
  6. I. Определение, классификация, этиология и
  7. V. Задания на определение количества и типы образующихся гамет
  8. VI. ОСНОВНЫЕ ПРИНЯТЫЕ СРЕДСТВА ЛЕЧЕНИЯ РАКОВЫХ ЗАБОЛЕВАНИЙ. ИОНИЗИРУЮЩИЕ ИЗЛУЧЕНИЯ И ГИПЕРБАРИЧЕСКАЯ ОКСИГЕНАЦИЯ ПРОТИВ РАКА — ОШИБКИ ОНКОЛОГИИ
  9. VII. Определение IgE
  10. Алкоголизм (определение, стадии развития, отличия от бытового пьянства). Течение и прогноз.

 

Полученная средняя арифметическая М при повторных исследованиях под влиянием случайных явлений может колебаться на ту или иную величину. Это обусловлено тем, что исследуется, как правило, только часть изучаемых явлений, то есть выборочная совокупность. Сумма же всех единиц, представляющих изучаемое явление, называется генеральной совокупностью. Результаты, полученные на основе выборочной совокупности, как правило, переносятся на генеральную совокупность. Чтобы определить степень точности выборочного наблюдения, необходимо оценить величину ошибки, которая может случайно произойти в процессе выборки. Такие ошибки носят название случайных ошибок репрезентативности т или средней ошибки средней арифметической. Они фактически являются разностью между средними числами, полученными при выборочном статистическом наблюдении, и аналогичными величинами, которые были бы получены при сплошном исследовании того же объекта (т. е. при исследовании генеральной совокупности).

Ошибки репрезентативности нельзя смешивать с ошибками регистрации или ошибками внимания (описки, просчеты, опечатки и др.), которые должны быть сведены до минимума.

Ошибки репрезентативности вытекают из самой сущности выборочного исследования. С помощью ошибок репрезентативности числовые характеристики выборочной совокупности распространяются на всю генеральную совокупность, то есть она характеризуется с учетом определенной погрешности.

Величины ошибок репрезентативности определяются как объемом выборки, так и разнообразием признака. Чем больше число наблюдений, тем меньше ошибка, чем больше изменчив признак, тем больше величина статистической ошибки.

На практике для определения средней ошибки выборки в статистических исследованиях пользуются следующей формулой:

где m — ошибка репрезентативности

σ — среднее квадратическое отклонение;

n — число наблюдений в выборке (при числе наблюдений менее 30 в подкоренное выражение вносится значение п-1).

Из формулы видно, что размер средней ошибки прямо пропорционален среднему квадратичному отклонению, т. е. вариабельности изучаемого признака, и обратно пропорционален корню квадратному из числа наблюдений.

Для рассматриваемого нами случая ошибка репрезентативности равна:

 

 

Дата добавления: 2015-02-02 | Просмотры: 1056 | Нарушение авторских прав


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

При использовании материала ссылка на сайт medlec.org обязательна! (0.003 сек.)