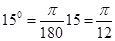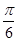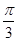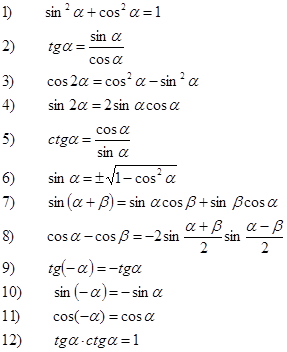|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Основные тригонометрические тождества. Зависимость между основными тригонометрическими функциями.Тригонометрические преобразования(теория) Решение задач на зависимость между радианной и градусной мерой угла. Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан. Найдем градусную меру угла в 1 радиан. Так как дуга длиной πR (полуокружность) стягивает центральный угол в 180⁰, то дуга длиной R стягивает угол в π раз меньший, т.е. Для упрощения в формулах (1,2) Пример 1. Найти градусную меру угла, равного 1) π, 2) Решение: По формуле (1) находим: 1) π=180⁰ 2) Пример 2. Найти радианную меру угла, равного 1)45⁰, 2)15⁰ Решение: По формуле (2) находим: 1) Таблица наиболее часто встречающихся углов в градусной и радианной мере.
Основные тригонометрические тождества. Зависимость между основными тригонометрическими функциями. Из определений синуса, косинуса, тангенса и котангенса сразу следуют основные тригонометрические тождества:
Дата добавления: 2016-03-26 | Просмотры: 417 | Нарушение авторских прав |
 (1). Если угол содержит α градусов, то его радианная мера равна
(1). Если угол содержит α градусов, то его радианная мера равна 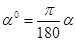
 (2)
(2)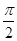 , 3)
, 3) 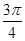
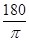 )=135⁰
)=135⁰ ; 2)
; 2)