 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Используя основные тригонометрические тождества, необходимо преобразовать выражения.Пример 3. Используя основное тригонометрическое тождество и формулу двойного угла, преобразуем данное выражение: 1) Пример 4. Используя формулу двойного угла и алгебраическую формулу разности квадратов, преобразуем данное выражение: Формулы суммы и разности синусов. Суммы и разности косинусов.
Пример 5. Вычислим, используя формулу суммы синусов: Формулы сложения
Пример 6. Вычислим, используя формулу сложения sin: Пример 7. Вычислим, используя формулу разности sin:
Формулы приведения Тригонометрическую функцию, под знаком которой содержится выражение вида 1) Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить; 2) Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида 3) Перед полученной функцией от аргумента тэ надо поставить тот знак, который имеет исходная функция при условии, что 0< t < Любая из формул приведения может быть записана и для градусной меры угла, то есть когда под знаком тригонометрической функции записано выражение вида 90° + α, 90° - α, 180° + α и т. д. Пример 8. cos (π + t). Наименование функции сохраняется, то есть получаем cos t. Далее, если считать, что 0< t < Пример 9. Преобразуем sin ( sin ( А сейчас получим пару новых формул приведения, воспользовавшись сформулированным правилом. Пример 10. Преобразуем tg ( Формулы приведения можно применять и в тех случаях, когда вместо аргумента t стоит более сложное выражение. Пример 11. сtg (360° + ПРИМЕР 12. Вычислить с помощью формул приведения sin (-330°) Решение Наименование функции сохраним. 330° = 360° - 30°- аргумент четвертой четверти, а в ней исходная функция синус имеет знак «минус». Этот знак надо поставить перед полученной функцией. Поэтому sin (-330°) = - sin 330° = - sin (360° - 30°) = - (- sin 30°) = - (- Пример 13. Докажите тождество Решение. Используя формулы приведения преобразуем левую часть тождества, а именно в числителе sin 140º= sin(90º+50º)=cos 50º В знаменателе cos 103º= cos(180º-50º)= –cos50º
Задания 1. Перевести в радианную меру угла: 2700, 1500, 1350 2. Перевести в градусную меру угла: 3. Упростить выражение: 4. Преобразовать выражение: 5. Преобразовать выражение: 6. 7. Вычислить: 8.Преобразуйте данные выражение с помощью формул приведения 1) cos 6) sin Дата добавления: 2016-03-26 | Просмотры: 759 | Нарушение авторских прав |
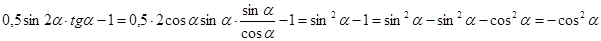
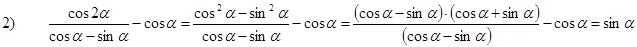
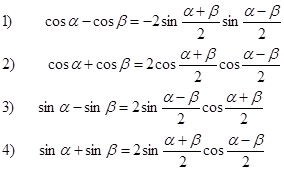
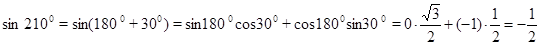
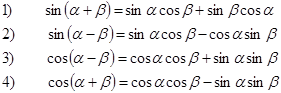
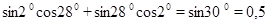
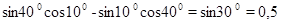
 ± t, где n – целое число, можно привести к более простому виду, такому что под знаком тригонометрической функции будет только аргумент t. Такие формулы обычно называют формулами приведения. Формул приведения очень много. Можно составить таблицу формул приведения, но пользоваться ею неудобно, так как она очень громоздка. Чтобы использовать формулы приведения, не заучивая их, полезно знать мнемоническое правило (правило, которое облегчает запоминание):
± t, где n – целое число, можно привести к более простому виду, такому что под знаком тригонометрической функции будет только аргумент t. Такие формулы обычно называют формулами приведения. Формул приведения очень много. Можно составить таблицу формул приведения, но пользоваться ею неудобно, так как она очень громоздка. Чтобы использовать формулы приведения, не заучивая их, полезно знать мнемоническое правило (правило, которое облегчает запоминание): ,
,  , то наименование тригонометрической функции следует изменить на родственное (синус меняется на косинус, тангенс на котангенс и наоборот);
, то наименование тригонометрической функции следует изменить на родственное (синус меняется на косинус, тангенс на котангенс и наоборот);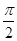 .
.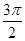 + t). Наименование функции следует изменить: получим сtg t. Далее, если считать, что 0< t <
+ t). Наименование функции следует изменить: получим сtg t. Далее, если считать, что 0< t <  ). Наименование функции сохраним (триста шестьдесят градусов равно двум пи): получим сtg
). Наименование функции сохраним (триста шестьдесят градусов равно двум пи): получим сtg  , Так как для синуса справедливо, что sin (-330°) = - sin 330°.Триста тридцать градусов распишем как разность трехсот шестидесяти и тридцати: sin (-330°) = - sin 330° = - sin (360° - 30°).
, Так как для синуса справедливо, что sin (-330°) = - sin 330°.Триста тридцать градусов распишем как разность трехсот шестидесяти и тридцати: sin (-330°) = - sin 330° = - sin (360° - 30°). ) =
) = 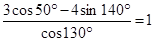


 =
= 
 ,
,  ,
,  ;
;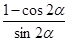
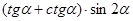
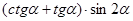
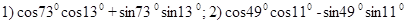
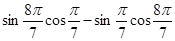
 ; 2) sin
; 2) sin  ; 3) ctg
; 3) ctg  ; 4) cos
; 4) cos  ; 5) tg
; 5) tg  ;
; ; 7) tg
; 7) tg  ; 8) cos(t-900);
; 8) cos(t-900);