 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Средняя арифметическаяСредняя арифметическая является наиболее распространенным видом средних величин, она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Чтобы исчислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число. Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой, служит простая средняя арифметическая. Средняя арифметическая простая применяется в тех случаях, когда исходные данные представляют собой несгруппированные индивидуальные значения признака, она определяется как отношение суммы отдельных значений осредняемого признака к общему числу этих значений:
где х1,х2,..., хп — индивидуальные значения варьирующего признака (варианты); п — число единиц совокупности. Пример 5.1. Требуется найти среднюю выработку одного рабочего (слесаря), если известно, сколько деталей изготовил каждый из 15 рабочих, т.е. дан ряд индивидуальных значений признака, шт.: 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20. Средняя арифметическая простая рассчитывается по формуле (5.4), шт.:
Средняя арифметическая взвешенная применяется в тех случаях, когда исходные данные представляют собой сгруппированные значения признака, т.е. дискретный или интервальный вариационный ряд распределения, она рассчитывается по формуле:
где f1,f2,...,fn — веса (частоты повторения одинаковых признаков);
Пример 5.2. Технику вычисления средней арифметической взвешенной проиллюстрируем на рассмотренном выше примере 1. Для этого сгруппируем исходные данные, образовав дискретный ряд распределения (графа 1,2 таблицы 5.1).
Таблица 5.1 – Распределение рабочих по выработке деталей
По формуле (5.5) средняя арифметическая взвешенная составит, шт.:
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Тогда формула средней арифметической взвешенной будет иметь вид:
где Иногда приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним), т.е. среднюю из средних. Средние из средних рассчитываются так же, как и средние из первоначальных значений признака. При этом средние, которые служат для исчисления на их основе общей средней, принимаются в качестве вариантов. Вычисление средней арифметической взвешенной из групповых средних
где f – число единиц в каждой группе. Если расчет средней арифметической взвешенной осуществляется по интервальному ряду распределения, т.е. значения осредняемого признака заданы в виде интервалов («от — до»), вычислительные операции должны проводиться в следующем порядке: - если в ряду распределения имеются открытые интервалы, их необходимо сделать закрытыми, при этом величины открытых интервалов (первый и последний) условно приравниваются к интервалам, примыкающим к ним (второй и предпоследний); - от интервального ряда необходимо перейти к дискретному путем замены интервальных значений признака величиной середины интервала, т.е. их средними значениями (простая средняя между верхней и нижней границами каждого интервала); - рассчитать среднюю арифметическую взвешенную по формуле 5.5 Пример 5.3. Рассчитаем средний уровень оплаты труда (среднюю заработную плату) работников по данным таблицы 5.2, графа 1,2. В графах 3-5 реализованы расчетные процедуры, приведенные выше: - в графе 3 открытые интервалы преобразованы в закрытые: до 15 (10-15); свыше 30 (30-35); - в графе 4 рассчитаны середины интервалов; - в графе 5 определены произведения вариантов на частоты (
Таблица 5.2 – Распределение работников по уровню оплаты труда
Рассчитаем средний уровень оплаты труда:
Итак, средний уровень оплаты труда работников составляет 24,65 тыс. руб. в месяц. Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчета средней можно упростить и облегчить, если воспользоваться ее свойствами. Приведем (без доказательства) некоторые основные свойства средней арифметической. Свойство 1. Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз. Свойство 2. Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А. Свойство 3. Если веса всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится. Дата добавления: 2016-06-06 | Просмотры: 422 | Нарушение авторских прав |
 (5.4)
(5.4)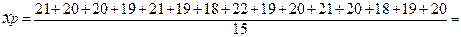
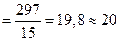
 (5.5)
(5.5) – сумма произведений величины признаков на их
– сумма произведений величины признаков на их – общая численность единиц совокупности.
– общая численность единиц совокупности.
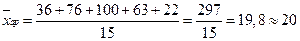
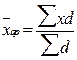 (5.6)
(5.6) – частость (в процентах или долях единицы).
– частость (в процентах или долях единицы). осуществляется по формуле:
осуществляется по формуле: (5.7)
(5.7) = 2465:100=24,65 тыс.руб.
= 2465:100=24,65 тыс.руб.