 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Средняя гармоническаяСредняя гармоническая представляет собой среднюю из обратных варьирующих значений признака, она применяется в тех случаях, если неизвестна численность изучаемой совокупности. Когда статистическая информация не содержит частот f по отдельным вариантам х совокупности, а представлена как их произведение w = x · f, применяется формула средней гармонической взвешенной:
где w1, w2, … wn – значение осредняемого признака, взвешенное на их число, т.е. w = x · f; Таким образом, средняя гармоническая применяется тогда, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины. Пример 5.4. По данным (таблицы 5.3) требуется определить среднюю цену 1 кг яблок в апреле. Средняя цена 1 кг яблок, (руб.), по трем коммерческим магазинам может быть исчислена по формуле (5.8) средней гармонической взвешенной:
Таблица 5.3 - Цена и выручка от реализации по трем коммерческим магазинам
В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:
где по одному разу; п — число вариантов. Для закрепления знаний по теме рассмотрим задачу на применение в расчетах средней арифметической и средней гармонической. Пример 5.5. Требуется определить средний размер двух видов вклада в банке в октябре и ноябре по данным таблицы 5.4.
Таблица 5.4 – Информация о вкладах в банке для расчета средних значений
В октябре для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной, тыс. руб.:
Средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной, тыс. руб.:
Как отмечено ранее, к числу степенных средних относятся также средняя геометрическая, средняя квадратическая, средняя кубическая. Эти виды средних величин имеют относительно ограниченное применение в статистическом анализе и рассчитываются по формулам, представленным в таблице 5.5. Таблица 5.5 – Методика расчета средней геометрической, средней квадратической и средней кубической
5.2.2 Структурные средние Особым видом средних величин являются структурные средние, которые применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К классу структурных средних относятся мода и медиана. Мода (M0) - значение признака, наиболее часто встречающееся в ряду распределения. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п. В дискретном вариационном ряду мода - это варианта, имеющая наибольшую частоту. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
где Модальный интервал определяется по наибольшей частоте. Пример 5.6. Группировка предприятий по стоимости основных производственных фондов (ОПФ) представлена следующим распределением (таблица 5.6). Таблица 5.6 – Распределение предприятий региона по стоимости основных производственных фондов (ОПФ)
По данным таблицы 5.6 видно, что модальным является интервал: 18-20, т.к. он имеет наибольшую частоту. Рассчитаем моду, млн. руб.:
Итак, модальным значением стоимости ОПФ предприятий является стоимость, равная 18,8 млн. руб. Медиана (Ме) - это варианта, который находится в середине вариационного ряда. Медиана делит рад на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного рада. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы. Пример 5.7. Пусть ряд состоит из показателей цены товара в отдельных торговых точках города, руб.: 630, 650, 680, 690, 700, 710, 720, 730, 750. Номер медианы для нечетного объема вычисляется по формуле:
где n — число значений признака в ряду распределения. В нашем примере номер медианы равен 5, медиана равна 700 руб. (т.е. одна половина товара реализуется по цене менее 700 руб., а другая — более 700 руб.). В случае четного объема ряда распределения медиана равна средней из двух вариантов, находящихся в середине ряда. В интервальных рядах распределения медианное значение оказывается в каком-то из интервалов признака – в медианном интервале. Для определения медианного интервала необходимо определять накопленную (кумулятивную) частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы всех частот ряда. Значение медианы вычисляется по формуле:
где Пример 5.8. Рассчитаем медиану по данным табл. 5.6. Прежде всего, найдем медианный интервал. Таким интервалом, очевидно, будет интервал стоимости ОПФ предприятий (18-20 млн. руб.), поскольку его кумулятивная частота равна 18 (2+6+10), что превышает половину суммы всех частот (25: 2 = 12,5). Нижняя граница интервала 18 млн. руб., его частота 10; частота, накопленная до него, равна 8. Подставив данные в формулу (5.12), найдем значение медианы, млн. руб.:
Полученный результат говорит о том, что из 25 предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 млн. руб., а 12 предприятий - более. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить асимметрию ряда распределения. Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части — квартили, на пять равных частей - квинтили, на десять частей - децили, на сто частей — перцентили. Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет более глубоко и детально охарактеризовать изучаемую совокупность.
5.3 Показатели вариации Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д. Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Для оценки вариации в статистике применяют следующие показатели: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Простейшим показателем вариации является размах вариации (R), который представляет собой разность между максимальным и минимальным значениями признака: R =xmax - xmin Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака. Среднее линейное отклонение • для несгруппированных данных: где п — число членов ряда; • для сгруппированных данных: где Дисперсия признака (σ 2) представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): • простая дисперсия для несгруппированных данных:
• взвешенная дисперсия для сгруппированных данных:
Формула (5.15) применяется при наличии у вариантов своих весов (или частот вариационного ряда). Формулу для определения дисперсии (5.15 и 5.16) можно преобразовать, учитывая, что σ 2 = где
Тогда для сгруппированных данных формула дисперсии (5.17) имеет следующий вид:
т.е. дисперсия равна разности средней из квадратов вариантов и квадрата их средней. Среднее квадратическое отклонение (σ) равно корню квадратному из дисперсии:
• для несгруппированных данных: • для сгруппированных данных: Для осуществления сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации — коэффициент вариации. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %. Пример 5.9. Результаты обследования показали следующее распределение работников торговли по стажу, представленное в таблице 5.7: Таблица 5.7 - Распределение работников торговли по стажу работы
На основании этих данных исчислить: 1) средний стаж работников торговли; 2) дисперсию и среднее квадратическое отклонение; 3) коэффициент вариации; Средний стаж работников торговли для открытого интервального ранжированного ряда определим следующим образом. Открытые интервалы сделаем закрытыми (графа 1 таблицы 5.8) и определим середины интервалов (графа 3 таблицы 5.8) по методике рассмотренной в вопросе 2.1 данной темы. Рассчитаем средний стаж работников торговли по данным графы 3 таблицы 5.8 по формуле средней арифметической взвешенной:
Таблица 5.8 – Вспомогательные расчеты для определения показателей вариации
Чтобы исчислить дисперсию по формуле
3. Среднее квадратическое отклонение исчислим по формуле:
4. Коэффициент вариации определяется по формуле:
Вывод: проведенные расчеты коэффициента вариации свидетельствует, что уровень вариации стажа работы по изучаемой совокупности является относительно высоким (т.к. коэффициент вариации больше 33,3%). Другими словами совокупность является неоднородной в отношении анализируемого признака (стажа работы).
5.4 Использование показателей вариации в анализе взаимосвязей
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой. Общая дисперсия (σ2) измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней Межгрупповая дисперсия (δ2) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних
где f - численность единиц в группе. Внутригрупповая (частная) дисперсия σ2i отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xt (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
На основании внутригрупповой дисперсии по каждой группе, т.е. на основании σ2i можно определить общую среднюю из внутригрупповых дисперсий:
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака. Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (квалификационного разряда) на изучаемый признак (количество изготавливаемых изделий). Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (η2) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи - единице. Эмпирическое корреляционное отношение - это корень квадратный из эмпирического коэффициента детерминации:
η оно показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение η, как и η2, может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии (δ2 = σ2), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока: Таблица 5.9 – Шкала Чэддока
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Дата добавления: 2016-06-06 | Просмотры: 665 | Нарушение авторских прав |
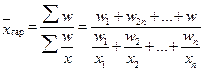 (5.8)
(5.8)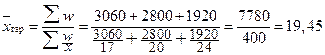 .
.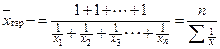 (5.9)
(5.9)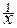 - отдельные варианты обратного признака, встречающиеся
- отдельные варианты обратного признака, встречающиеся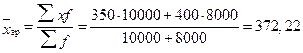
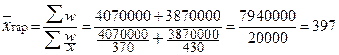 .
.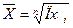

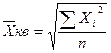
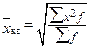
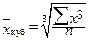
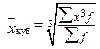
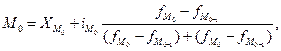 (5.10)
(5.10)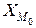 - нижняя граница модального интервала;
- нижняя граница модального интервала; 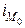 — модальный интервал;
— модальный интервал; 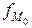 ,
, 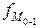 ,
, 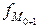 - частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).
- частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно).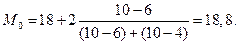
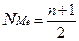 (5.11)
(5.11)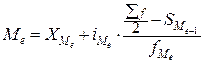 (5.12)
(5.12)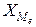 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; 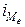 - величина медианного интервала;
- величина медианного интервала; 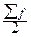 - половина от общего числа совокупности;
- половина от общего числа совокупности; 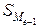 - накопленная частота интервала, предшествующего медианному;
- накопленная частота интервала, предшествующего медианному; 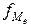 -частота медианного интервала.
-частота медианного интервала.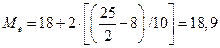 .
.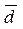 представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической, рассчитывается по формуле:
представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической, рассчитывается по формуле: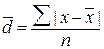 (5.13)
(5.13)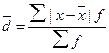 (5.14)
(5.14)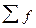 — сумма частот вариационного ряда.
— сумма частот вариационного ряда.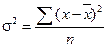 (5.15)
(5.15)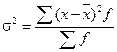 (5.16)
(5.16)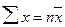 , тогда расчет дисперсии может быть осуществлен по формуле:
, тогда расчет дисперсии может быть осуществлен по формуле: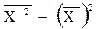 (5.17)
(5.17)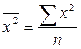 - для несгруппированных данных;
- для несгруппированных данных;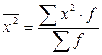 - для сгруппированных данных.
- для сгруппированных данных.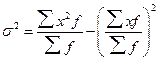 (5.18)
(5.18)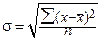 (5.19)
(5.19)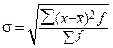 (5.20)
(5.20)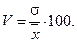 (5.21)
(5.21)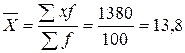 года.
года.
 =
=
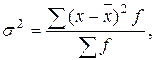 продолжим расчет показателей в табл. 5.8 (графа 5 – 7). Итог графы 7 подставим в формулу для дисперсии:
продолжим расчет показателей в табл. 5.8 (графа 5 – 7). Итог графы 7 подставим в формулу для дисперсии: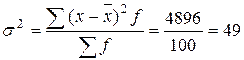 (лет).
(лет).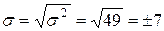 (лет)
(лет)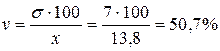
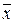 и может быть вычислена как простая дисперсия (по формуле (5.15) или взвешенная дисперсия по формуле (5.16).
и может быть вычислена как простая дисперсия (по формуле (5.15) или взвешенная дисперсия по формуле (5.16).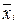 от общей средней
от общей средней 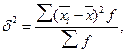 (5.22)
(5.22)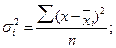 (5.23)
(5.23)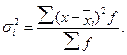 (5.24)
(5.24)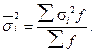 (5.25)
(5.25)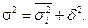 (5.26)
(5.26)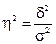 (5.27)
(5.27)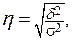 (5.28)
(5.28)