|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Логарифмическая функция
Определение 1. Функция, обратная к показательной функции 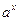 , называется логарифмической функцией и обозначается , называется логарифмической функцией и обозначается 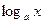 . .
Заметим, что данное определение корректно, т.е. логарифмическая функция существует в силу строгой монотонности показательной функции 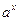 при при 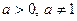 по теореме о существовании и непрерывности обратной функции. по теореме о существовании и непрерывности обратной функции.
Если 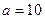 и и 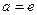 , то логарифмы называют десятичными и натуральными и обозначают , то логарифмы называют десятичными и натуральными и обозначают 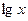 и и 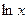 соответственно. соответственно.
Из свойств взаимно-обратных функций следует, что 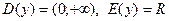 . Логарифмическая функция не является ни четной, ни нечетной. Непериодическая. По теореме о существовании и непрерывности обратной функции она непрерывна в области определения, то есть точек разрыва не имеет, при . Логарифмическая функция не является ни четной, ни нечетной. Непериодическая. По теореме о существовании и непрерывности обратной функции она непрерывна в области определения, то есть точек разрыва не имеет, при 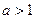 строго возрастает от строго возрастает от 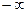 до до 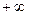 , при , при 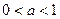 строго убывает от строго убывает от 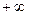 до до 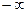 , поэтому точек экстремума не имеет. , поэтому точек экстремума не имеет. 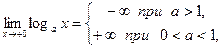 поэтому поэтому 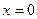 – вертикальная асимптота. – вертикальная асимптота. 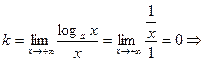 наклонных асимптот нет. наклонных асимптот нет. 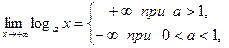  горизонтальных асимптот нет. горизонтальных асимптот нет. 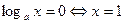 , так как , так как 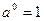 , то есть точка (1; 0) – точка пересечения графика с осью , то есть точка (1; 0) – точка пересечения графика с осью 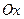 , с осью Оу пересечения нет, так как , с осью Оу пересечения нет, так как 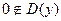 . . 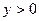 на на 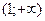 и и 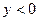 на (0; 1) при на (0; 1) при 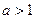 , а при , а при 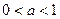 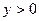 на (0; 1) и на (0; 1) и 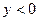 на на 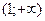 . . 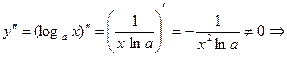 точек перегиба нет. Если точек перегиба нет. Если 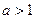 , то , то 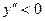 и кривая выпукла вверх в и кривая выпукла вверх в 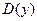 , если , если 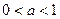 , то , то 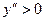 и кривая выпукла вниз в и кривая выпукла вниз в 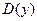 . .
 Заметим, что в силу свойства графиков взаимно-обратных функций кривые Заметим, что в силу свойства графиков взаимно-обратных функций кривые 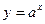 и и 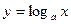 симметричны относительно прямой симметричны относительно прямой 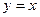 . .
   у у 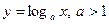
 О 1 х О 1 х
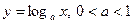
Справедливы следующие свойства логарифмов, известные из школьного курса математики:
1. 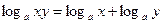 . .
2. 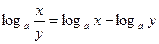 . .
3. 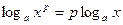 , где , где 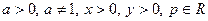 , а также формула перехода от одного основания логарифма к другому , а также формула перехода от одного основания логарифма к другому
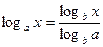 . .
Дата добавления: 2015-01-18 | Просмотры: 490 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|

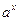 , называется логарифмической функцией и обозначается
, называется логарифмической функцией и обозначается 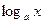 .
.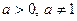 по теореме о существовании и непрерывности обратной функции.
по теореме о существовании и непрерывности обратной функции.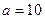 и
и 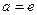 , то логарифмы называют десятичными и натуральными и обозначают
, то логарифмы называют десятичными и натуральными и обозначают 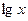 и
и 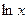 соответственно.
соответственно.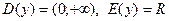 . Логарифмическая функция не является ни четной, ни нечетной. Непериодическая. По теореме о существовании и непрерывности обратной функции она непрерывна в области определения, то есть точек разрыва не имеет, при
. Логарифмическая функция не является ни четной, ни нечетной. Непериодическая. По теореме о существовании и непрерывности обратной функции она непрерывна в области определения, то есть точек разрыва не имеет, при 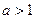 строго возрастает от
строго возрастает от 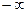 до
до 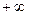 , при
, при 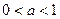 строго убывает от
строго убывает от 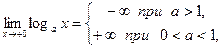 поэтому
поэтому 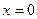 – вертикальная асимптота.
– вертикальная асимптота. 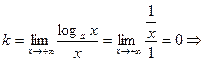 наклонных асимптот нет.
наклонных асимптот нет. 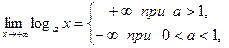
 горизонтальных асимптот нет.
горизонтальных асимптот нет. 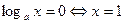 , так как
, так как 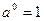 , то есть точка (1; 0) – точка пересечения графика с осью
, то есть точка (1; 0) – точка пересечения графика с осью 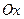 , с осью Оу пересечения нет, так как
, с осью Оу пересечения нет, так как 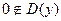 .
. 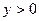 на
на 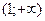 и
и 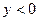 на (0; 1) при
на (0; 1) при 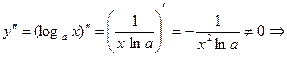 точек перегиба нет. Если
точек перегиба нет. Если 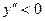 и кривая выпукла вверх в
и кривая выпукла вверх в 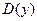 , если
, если 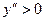 и кривая выпукла вниз в
и кривая выпукла вниз в  Заметим, что в силу свойства графиков взаимно-обратных функций кривые
Заметим, что в силу свойства графиков взаимно-обратных функций кривые 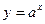 и
и 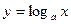 симметричны относительно прямой
симметричны относительно прямой 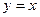 .
.

 у
у 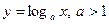
 О 1 х
О 1 х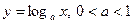
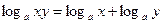 .
.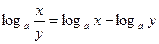 .
.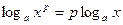 , где
, где 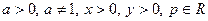 , а также формула перехода от одного основания логарифма к другому
, а также формула перехода от одного основания логарифма к другому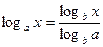 .
.