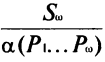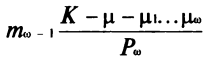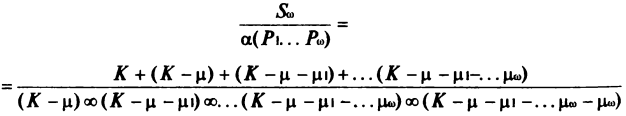|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Cisfinitum. Письмо к Леониду Савельевичу Липавскому. Падение ствола
Леонид Савельевич,
I
1) Будем считать всякую дисциплину творческой, если она не опирается на постулаты категории E. 2) Всякую дисциплину, опирающуюся на постулаты категории E, будем считать нетворческой. 3) Логическая наука («формальная логика», «законы мысли») опирается на постулаты категории E, следовательно она нетворческая. 4) Искусство не может опираться на постулаты категории E, следовательно оно есть творческая дисциплина. 5) Говорю о творческой науке, не могущей опираться на постулаты категории E.
II
Некий ствол стоит на постулате E. Создадим постулат E как первоначальный ствол. Тогда ствол E встанет на новый постулат P1. Создадим постулат P1 как первейший ствол. Тогда ствол E опрётся на постулат P2. Создадим постулат P2 как наипервейший ствол и т. д. Должен заметить, что тем и славен ствол формальной логики (Bool, Пирс и др.), что может не интересоваться происхождением постулата E. Постулаты E, EI, EII…могут быть в любой момент заменены P1, P2, P3 …и новые постулаты могут быть рассматриваемы как постулаты категории E. И только при бесконечном сдвигании P в последующие P1, P2, P3 …, ствол растёт или вернее падает в необрезанное поле постуляции, и постуляция принимает вид P1 P2 P3 …Pω. Изобразим новый ствол Sω. Обращаю внимание на то, что для того, чтобы создать поле (P1 …Pω), надо поочерёдно исследовать каждое P. Условимся исследованное поле отмечать буквой α. Тогда запишем, что новый ствол Sω опирается на исследованную постуляцию α (P1 …Pω) или
III
Определим исследование постулативного поля. Для этого определим постулат как предел падения опирающегося на него ствола. И заметим, что если ствол есть некий континуум K, то постулат будет выражен формулой K — μ = 1 (при любом μ). Принимаем (K — μ) за некий ствол и исследуя его, находим постулат P1. P1 = K — μ — μ1 = 1. Следуя дальше, получаем: P2 = K — μ — μ1 — μ2 = 1. Открывая падение, видим: Pω = K — μ — μ1 — μ2 … μω — μω = 1. И, наконец, исследование постулативного поля выразится[5]: α (P1 …Pω) = (K — μ) ∞ (K — μ — μ1) ∞ … (K — μ — μ1 …μω) ∞ (K — μ — μ1 …μω — μ)I
IV
Посмотрим, что происходит со стволом. Раньше всего назовём этот процесс — падение ствола. Последовательные моменты падения мы можем выразить так: 1. K постулируемый E, или K/E 2. (K — μ) / P1 3. (K — μ — μ1) / P2
Следуя дальше, получаем:
V
Меня очень интересует Ваше мнение по поводу непостулируемой науки. Ведь постулируя Sω бесконечно убывающим полем (P1 …Pω), мы не можем называть это прежней единицей опоры. Новая единица опоры будет 0 (нуль). α (P1 …Pω) = 0. Это первое и единственное утверждение, могущее быть новым постулатом не категории E. Согласно первому условию 1-го параграфа, ствол, опирающийся на a (P1 …Pω), будем считать творческим.
VI
Если допустить, что может существовать творческая наука Sω, то можно предвидеть, что она по 4-му условию § 1 будет схожа с искусством. Если творческой науке придётся иметь дело с понятиями количества, то можно предвидеть, что система счисления должна быть иной, нежели наш солярный корпус. Скромно замечу, что новая система счисления будет нулевая и область её исследования будет Cisfinitum.
На этом, дорогой Леонид Савельевич, разрешите кончить письмо и пожелать Вам спокойной ночи. Я же, раздумывая над цисфинитной пустотой, готов и постоять, пока люди, считая до ста, торопятся уснуть, а коварный Мукк со своими собаками собирается на охоту.
16 октября 1930.
Дата добавления: 2015-03-04 | Просмотры: 1003 | Нарушение авторских прав |