 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Тригонометрические уравненияУравнения, в которых переменная содержится под знаком тригонометрических функции, называются тригонометрическими. Познакомимся с простейшими тригонометрическими уравнениями. К простейшим тригонометрическим уравнениям относят уравнения вида sin (kx +m)=a, cos(kx +m)=a, tg(kx +m)=a, ctg(kx +m)=a. Мы уже изучили, что 1. Решения уравнения sin x =a, при | а | ≤ 1, имеют вид: х = (- 1)n arcsin a + πn. или эти решения можно записать по-другому х = arcsin a + 2πk, х = π - arcsin a + 2πk. 2. Решения уравнения cos x =a, при | а | ≤ 1, имеют вид: х = ±arccos a + 2πn. 3. Если | а |> 1, то уравнения sin x =a и cos x =a не имеют решений. 4. Уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn. 5. Уравнение ctg х = a имеет решение для любого значения а и эти решения имеют вид: х = arcсtg а + πn. 6. Важно помнить частные случаи:
Во всех формулах подразумевается, что n ϵZ, k ϵZ Дата добавления: 2016-03-26 | Просмотры: 346 | Нарушение авторских прав |
 + 2πn
+ 2πn
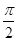 + 2πn
+ 2πn