 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Однородные тригонометрические уравненияРазберем, как решаются «Однородные тригонометрические уравнения». Это уравнения специального вида. Познакомимся с определением. Уравнение вида уравнение вида Если а=0, то уравнение примет вид b cos x = 0. Если b = 0, то получим а sin x= 0. Данные уравнения являются элементарными тригонометрическими, и их решение мы уже рассматривали. Рассмотримтот случай, когда оба коэффициента не равны нулю. Разделим обе части уравнения а sin x+b cos x = 0 почленно на cos x. Это мы можем сделать, так как косинус икс отличен от нуля. Ведь, если cos x = 0, то уравнение а sin x+b cos x = 0 примет вид а sin x = 0, а ≠ 0, следовательно sin x = 0. Что невозможно, ведь по основному тригонометрическому тождеству sin2 x+ cos2 x=1.
Разделив обе части уравнения а sin x+b cos x = 0 почленно на cos x, получим: Осуществим преобразования: 1. 3.Таким образом получим следующее выражение а tg x + b =0. Осуществим преобразование: 1.перенесем b в правую часть выражения с противоположным знаком а tg x =- b 2. Избавимся от множителя а разделив обе части уравнения на а Вывод: Уравнение вида а sin mx+b cos mx = 0 тоже называют однородным тригонометрическим уравнением первой степени. Чтобы решить его, делят обе части на cos mx. Пример 5. Решить уравнение Решение. Разделим обе части уравнения почленно на cos, получим Таки образом получили уравнение: Решение нашего уравнения будет иметь вид:
х=2 arctg Ответ: х=2 arctg Перейдем к однородному тригонометрическому уравнению второй степени а sin2 x+b sin x cos x +с cos2 x= 0. Рассмотрим несколько случаев. I. Если а=0, то уравнение примет вид b sin x cos x +с cos2 x= 0. При решении э то уравнения используем метод разложения на множители. Вынесем cos x за скобку и получим: cos x(b sin x +с cos x)= 0. Откуда cos x= 0 или b sin x +с cos x= 0. А эти уравнения мы уже умеем решать. Разделим обе части уравнения почленно на cosх, получим 1. 2. Таким образом получаем уравнение: b tg х+с=0
tg х=
II. Если а≠0, то обе части уравнения почленно разделим на cos2 x.
III. Если с=0, то уравнение примет вид а sin2 x+b sin x cos x= 0. Это уравнение решается методом разложения на множители (вынесем sin x за скобку). Пример 6. Решить уравнение Решение. Разложим на множители (вынесем за скобку cos x). Получим
Ответ: х = Задания
Домашнее задание 1. Решить уравнение: 2 cos 2. Решить уравнение: 3 sin 3. Решить уравнение: 2 sin 4. Решить уравнение: sin x+ 5. Решить уравнение: cos
Дата добавления: 2016-03-26 | Просмотры: 599 | Нарушение авторских прав |
 называют однородным тригонометрическим уравнением первой степени;
называют однородным тригонометрическим уравнением первой степени; называют однородным тригонометрическим уравнением второй степени.
называют однородным тригонометрическим уравнением второй степени.
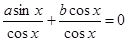
 ; 2.
; 2. 
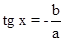
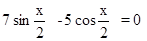
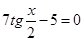 , Преобразуем выражение, перенесем минус пять в правую часть, изменив знак.
, Преобразуем выражение, перенесем минус пять в правую часть, изменив знак. 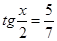
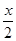 = arctg
= arctg  + πn, найдем х
+ πn, найдем х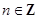
 .
.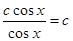
 Решение нашего уравнения будет: х = arctg
Решение нашего уравнения будет: х = arctg 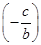 + πn,
+ πn, 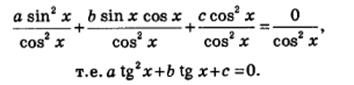
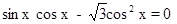
 , т.е. cos x=0 или
, т.е. cos x=0 или 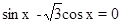
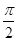 + πn
+ πn
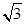 =0,
tg х =
=0,
tg х = 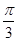 + πn
+ πn
 =0
=0
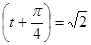
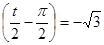
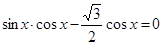

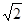
 x + sin x+1=0
x + sin x+1=0 sin 2x
sin 2x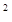 x – 10 cos x+3=0
x – 10 cos x+3=0