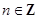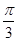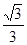|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Рассмотрим примеры.Пример 1. Решить уравнение Решение. Введем новую переменную t = 4x, получим sin t = Тогда t =(–1)n arcsin ЗАМЕЧАНИЕ. Необязательно вводить новую переменную. Можно сразу от уравнения sin 4x = Пример 2. Найти те корни уравнения sin 4x = Решение. Как мы знаем из примера 1, решение уравнения sin 4x = 1) если n=0, х = (- 1)0 2) если n =1, х=(–1)1 3) если n =2, х =(- 1)2 4) рассмотрим n = - 1, х =(- 1)- 1 Итак, заданному отрезку [0, Ответ: Для решения тригонометрических уравнений чаще всего используют метод введения переменной или метод разложения на множители. Пример 3. Решим уравнение tg Решение. Используем метод введения переменной. Пусть у = tg сtg Вернемся к переменной x и получим два уравнения tg Так как уравнение tg x = a имеет решение для любого значения а и эти решения имеют вид х = arctg x a + πn, то для первого уравнения имеем: Для второго уравнения имеем: Ответ: х = Пример 4. Решить уравнение 2 cos х sin 7x - sin 7x = 0.(два косинус икс на синус семи икс минус синус семи икс равно нулю) Решение. Используем метод разложения на множители. Вынесем за скобку sin 7x, получим sin 7x(2cos х – 1)=0. Перейдем к совокупности уравнений: sin 7x = 0; 2 cosх – 1=0 2 cosх = 1 cosх = Так как мы помним, что при а=0, х = πn,
то из первого уравнения находим, что 7х = πn, значит, х = Так как Решения уравнения cos x =a, при | а | ≤ 1, имеют вид: х = ±arccos a + 2πn, а а= А так как из определения арккосинуса числа а следует, что arccos ЗАМЕЧАНИЕ. При переходе от уравнения вида f1(x) ∙ f2(x) = 0 нужно быть очень внимательным. Рассмотрим, например, уравнение ctgх(cosх – 1) =0. 1. Перейдем к совокупности уравнений: сtg х=0. cosх – 1=0. cos х =1 Из уравнения ctg х= 0 находим по таблице значений котангенса: arcctg 0=
а из уравнения cos х =1 находим х Вспоминаем частные случаи, значит х= 2πn. Но включить в ответ второе решение нельзя, потому что при значениях х = 2πn множитель ctgх не имеет смысла, т.е. значения х = 2πn не принадлежат области определения уравнения (или по-другому области допустимых значений – ОДЗ). Значит х = 2πn - это посторонние корни. Ответ: х = Дата добавления: 2016-03-26 | Просмотры: 386 | Нарушение авторских прав |
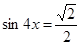 .
. . Так как |а|=
. Так как |а|= 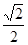 , значит | а | ≤ 1 и решение уравнения имеет вид х = (–1)n arcsin a + πn.
, значит | а | ≤ 1 и решение уравнения имеет вид х = (–1)n arcsin a + πn.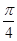 , то t = (–1)n
, то t = (–1)n 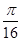 +
+  .
.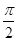 ].
].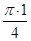 == –
== – 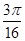 . Это число принадлежит заданному отрезку [0,
. Это число принадлежит заданному отрезку [0,  . Это число не принадлежит заданному отрезку [0,
. Это число не принадлежит заданному отрезку [0, 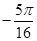 . Это число не принадлежит заданному отрезку [0,
. Это число не принадлежит заданному отрезку [0, 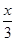 + 2 сtg
+ 2 сtg 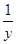 (так как tg t ∙ сtg t = 1). Получим уравнение у +
(так как tg t ∙ сtg t = 1). Получим уравнение у + 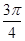 + 3πn.
+ 3πn.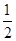 .
. .
.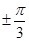 + 2πn.
+ 2πn.