 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Теоретичні відомостіВідношення питомих або молярних теплоємностей γ = Cp/CV відіграє велику роль в адіабатичних процесах або в процесах, близьких до них. За значенням γ = Cp/CV визначають швидкість розповсюдження звуку в газах, від нього залежить течія газів по трубах зі звуковими швидкостями і досягнення надзвукових швидкостей в трубах, що розширюються. Адіабатичним називають процес, який проходить без теплообміну із зовнішнім середовищем. Залежність між параметрами газу в адіабатичному процесі визначають за рівнянням Пуассона: де p, V – відповідно тиск та об'єм газу; γ – коефіцієнт Пуассона (показник адіабати), який дорівнює відношенню питомої (молярної) теплоємності при сталому тиску до питомої (молярної) теплоємності при сталому об’ємі, тобто γ = Cp/CV. Питома теплоємність – це величина, яка дорівнює кількості теплоти δQ, необхідної для нагрівання одиниці маси речовини на 1 К: с = δQ/(mdT). Молярна теплоємність речовини – величина, яка дорівнює кількості теплоти δQ, необхідної для нагрівання 1 моля речовинина 1 К:
Молярна (С) та питома (с) теплоємності пов’язані між собою співвідношенням C = μс. Теплоємність газу залежить від умов його нагрівання. Для нагрівання однієї і тієї ж маси газу до однакової температури при ізобаричному процесі треба витратити більше теплоти, ніж при ізохоричному, бо при ізобаричному процесі, крім витрати теплоти на зміну внутрішньої енергії (збільшення температури), теплота витрачається і на зовнішню механічну роботу (чого нема при ізохоричному процесі). Тому молярна теплоємність ідеального газу при сталому тиску Cp більша за його молярну теплоємність при сталому об’ємі CV на універсальну газову сталу: Cp= CV+ R. Це співвідношення називають рівнянням Майєра. Його можна вивести з I закону термодинаміки: кількість теплоти δQ, яку одержує система, витрачається на зміну її внутрішньої енергії dU та на виконання роботи δA проти зовнішніх сил: δQ = dU + δA. (162.1) При ізобаричному процесі δA = pdV = тоді δQр = Якщо газ нагрівають при сталому об’ємі, то δА= 0, і тоді згідно I закону термодинаміки: dQV = CV Підставимо формули (162.2) – (162.4) в (162.1) і одержимо рівняння Майєра. Згідно з класичною молекулярно-кінетичною теорією молярна теплоємність при сталому об'ємі
а молярна теплоємність при сталому тиску де і – число ступенів вільності молекули (кількість незалежних координат, які визначають положення молекули у просторі). Для одноатомних молекул газу і = 3; для двохатомних і = 5; для трьох- і більше атомних і = 6. Тоді показник адіабати ідеального газу За формулою (162.5) можна теоретично визначити показник адіабати, якщо повітря прийняти за двохатомний газ. Дата добавления: 2016-06-05 | Просмотры: 469 | Нарушение авторских прав |
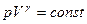
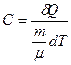
 RdT (162.2)
RdT (162.2) ,
, ,
, . (162.5)
. (162.5)