|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Рентгеновская дифрактометрия
5.1. Основные принципы рентгеновской дифрактометрии Рентгеновский структурный анализ представляет собой совокупность методов исследования структуры вещества по распределению в пространстве и интенсивностям рентгеновского излучения, рассеянного на объекте. Наряду с нейтронографией и электронографией рентгеноструктурный анализ является дифракционным методом, основанным на взаимодействии рентгеновского излучения с электронами вещества. Дифракционная картина зависит от длины волны рентгеновских лучей и строения вещества. Для исследования атомной структуры применяют излучение с длиной волны ≈1А°, т.е. порядка размеров атомов. Методами рентгеноструктурного анализа изучают металлы, сплавы, минералы, неорганические и органические соединения, полимеры аморфные вещества, жидкости и газы, молекулы белков, нуклеиновых кислот и т.д. при этом определяют минералогический (фазовый) качественный и количественный состав, ориентацию и размеры кристаллитов и коллоидных частиц, строение аморфных и полуаморфных материалов, атомную структуру кристаллов; измеряют внутренние напряжения, коэффициенты термического расширения; исследуют твердые растворы, и превращения, происходящие в материалах под влиянием температуры, давления, влажности и т.д. Рентгеновские лучи, проходя через кристаллическое вещество, рассеиваются его атомами. Рассеяние происходит на электронах атомов, которые становятся источниками сферических волн вторичного рентгеновского излучения. Интерференция этих волн приводит к возникновению дифракционной картины, интенсивность и пространственное расположение максимумов которой определяются атомной структурой вещества. Изучение рентгеновских дифракционных картин позволяет определять атомную структуру кристаллических веществ. Для такого рода исследований необходимо знать теорию дифракции рентгеновских лучей. Вначале рассмотрим геометрические условия возникновения дифракционной картины, приняв следующие упрощающие предположения: 1) падающие на кристалл рентгеновские лучи строго параллельны и монохроматичны; 2) электроны, принадлежащие данному атому, сосредоточены в геометрической точке – в узле кристаллической решетки; 3) кристаллическая решетка примитивна; 4) атомы кристалла неподвижны; 5) поглощение рентгеновских лучей в кристалле отсутствует; 6) кристалл имеет идеальное строение (отсутствует мозаичность); 7) размеры кристалла малы по сравнению с расстоянием до точки наблюдения; 8) вторичные (рассеянные) волны не взаимодействуют с падающей волной рентгеновского излучения. Перечисленные допущения не вносят изменения в вычисляемую геометрию расположения дифракционных максимумов, но сказываются на их интенсивности. Впоследствии неточности, связанные с определением интенсивности максимумов, будут устранены введением различных множителей интенсивностей. Теория, не учитывающая взаимодействия между первичным и рассеянным излучением, называется кинематической в отличие от динамической, в которой это взаимодействие учитывается.
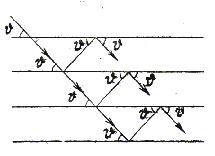
5.2. Подход Вульфа-Брэггов Дифракция рассматривается как результат взаимодействия волн после их зеркального отражения от атомных плоскостей.
Рис. 5.1. Атомная плоскость – воображаемая плоскость, которую можно провести через атомы, из которых состоит кристаллическая решетка. Уравнение Вульфа-Брэггов описывает распределение максимумов дифракционной картины. Условие возникновения максимумов – синфазность отраженных волн (рисунок). Условие дифракции – на разности хода 2-х лучей должно укладываться целое число длин волн дифрагирующего РИ, то есть
если разность хода выразить через межплоскостное расстояние
то получим уравнение Вульфа-Брэгга
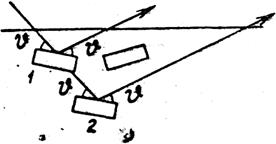
dhkl A C B
Рис. 5.2. Схема, поясняющая уравнение Вулфа Брэгга Используя это уравнение можно решать задачи рентгеноструктурного анализа – послать на исследуемый кристалл пучок рентгеновского излучения с известной длиной волны l под определенным углом Q можно рассчитать межплоскостные расстояния dhkl для этого кристалла и потом с их помощью определить параметры его элементарной ячейки. Такой подход прост, но дает довольно ограниченные результаты. Богаче его, но сложнее подход Лауэ. 5.3. Подход Лауэ Рассмотрим возникновение дифракции на одномерной решетке (цепочке атомов).
Ŝ0 a a0
Ŝ1 Ŝ1
Рис. 5.3. Схема, поясняющая подход Лауэ.
На одномерную решетку с периодом а падает РИ с длиной волны l. Для дифракции надо, чтобы амплитуды складывались, то есть разность хода составляла целое число длин волн (аналогично уравнению В-Б), то есть разности длин векторов S и S1:
где Ŝ1- Ŝ0 – разность векторов, а âŜ - скалярное произведение векторов. Из этого можно выразить угол a, под которым будет возникать дифракция:
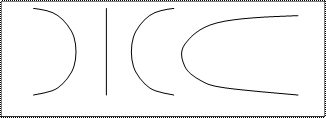
Очевидно, что рассеянное излучение, для которого будет выполняться условие дифракции, будет образовывать систему конусов:
Н=0 Н=1 Н=2
Рис. 5.4. К возникновению интерференционной картины по Лауэ Сечение конуса плоскостью дает гиперболу. Далее рассмотрим дифракционная картина от двумерной решетки. Уравнение дифракции для второй координаты можно записать в виде
Тогда дифракционная картина на рентгенопленке – не гиперболы, а следы их пересечений – точки.
Рис. 5.5. Возникновение дифракционной картины от двумерной решетки Аналогично для трехмерной решетки:
Тогда дифракционная картина на рентгенопленке – не гиперболы, не точки, а мало точек – продукт пересечения трех семейств гипербол. Система уравнений
называется системой уравнений Лауэ. Индексы HKL – индексы Лауэ, при этом связь индексов Миллера и Лауэ:
Реализация дифрактометрии: облучаем кристалл пучком рентгеновского излучения, получаем дифракционную картину. Далее по дифракционной картине можно: определить тип элементарной ячейки, определить межплоскостные расстояния (размеры элементарной ячейки), используя базы дифрактограмм определить состав исследуемого кристалла. Чтобы реализовать методы Лауэ и Вульфа-Брэгга целесообразно ввести понятие обратной решетки. Обратной решеткой называют связанную с кристаллом некую гипотетическую пространственную точечную решетку, обладающую следующими свойствами: 1) радиус-вектор обратной решетки 2) длина вектора обратной решетки определяется соотношением:
где Индексы узлов в обратной решетке НКL равны соответствующим индексам Лауэ в теории интерференции. Плоскостям прямой решетки соответствуют узлы в обратной и наоборот. Обратная решетка строится на осях
Интерференционную функцию Лауэ можно записать в виде
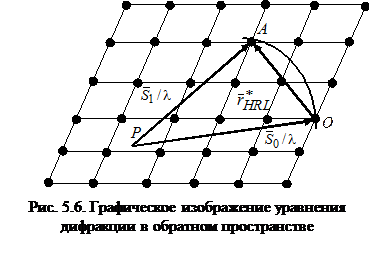
тогда она эквивалентна трем уравнениям Лауэ. Умножив скалярно левую и правую части уравнения на Для удобства понимания рассмотрим геометрическую интерпретацию условия «отражения» рентгеновских лучей, использую представление об обратной решетке. На рис. 5.6. показан участок одной из её плоскостей. Примем узел 0 за начало координат пространства обратной решетки и построим в направления первичного пучка рентгеновских лучей Опишем вокруг начала Р вектора
Сечение сферы плоскостью чертежа дает окружность. Сфера распространения всегда проходит через начальный узел 0. Если сфера распространения пересекает еще какой-нибудь узел, например А, то возможно появление дифракционного максимума в направлении
Таким образом, для того, чтобы рентгеновские лучи отражались от какой-нибудь атомной плоскости (hkl), сфера распространения, кроме начала координат, должна проходить также через соответствующий данной плоскости узел обратной решетки HKL, соединенный с началом координат вектором
Если на неподвижной монокристалл направлен пучок монохроматических рентгеновских лучей, то в общем случае ни один из узлов обратной решетки может не оказаться на сфере распространения – никакого отражения при этом не будет. Для того, чтобы получить отражение от одной или нескольких атомных плоскостей, необходимо добиться выхода одного или нескольких узлов обратной решетки на сферу, распространения. С этой целью нужно, либо использовать пучок лучей с непрерывным спектром тормозного излучения, либо тем или иным способом менять ориентировку кристалла по отношению к монохроматическому пучку рентгеновских лучей. Методы получения дифракционных рентгенограмм различаются способами выведения узлов обратной решетки на поверхность сферы распространения.
5.4. Методы рентгеновской дифрактометрии
Метод Лауэ. В методе Лауэ дифракционная картина возникает от неподвижного монокристалла при облучении его тормозным рентгеновским излучением. Непрерывный спектр тормозного излучения реальной рентгеновской трубки имеет длинноволновую и коротковолновую границы. Первая, lmах, определяется поглощением в выходном окне рентгеновской трубки, вторая, lмин — максимальным значением ускоряющего напряжения. Поэтому в пространстве обратной решетки можно провести бесконечное число сфер распространения, ограниченных с одной стороны сферой радиуса
Положение максимума, обусловленного, например, узлом HKL, можно найти следующим образом. Проведем в узел HKL из начального узла 0 вектор обратной решетки Наблюдаемую по методу Лауэ дифракционную картину можно зарегистрировать на плоской фотопленке, расположенной перпендикулярно к первичному пучку (перед или за монокристаллом по ходу первичного пучка). Метод Лауэ находит применение на первом этапа изучения атомной структуры кристаллов. С его помощью определяют ориентировку кристаллографических осей в неограненном монокристалле. Кроме этого, форма пятен лауэграммы позволяет судить о степени совершенства кристалла.
Метод вращающегося монокристалла. В методе вращающегося монокристалла используют пучок характеристического излучения, который направляют перпендикулярно оси вращения, а дифракционную картину регистрируют на фотопленке,, расположенной вокруг кристалла. Ось кассеты совпадает с осью вращения. Возникновение дифракционной картины интерпретируется геометрически с помощью понятия обратной решетки. Пусть например, кристалл вращается вокруг оси
Рис. 5.8. Возникновение дифракционной картины в методе вращения монокристалла Направим первичный пучок рентгеновских лучей нормально оси
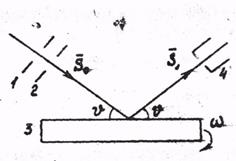
Метод широко расходящегося пучка. Одним из наиболее перспективных направлений рентгенографии монокристаллов является то направление, в котором используется широкоугловая (трехмерная) дифракция, осуществляемая за счет большой расходимости по всем направлениям падающего на кристалл рентгеновского излучения. Это направление реализовано в методе ШРП. Различают две разновидности экспериментального воплощения этого метода. Первый вариант - пучок быстрых электронов
Рис. 5.9. Схемы съемки в широко расходящемся пучке В этом случае характеристическое излучение возникает в веществе кристалла, играющего роль мишени рентгеновской трубки. Регистрируемые на фотопленке 2 по направлению Неудобство связано с необходимостью помещения образца в вакуум. Кроме того, воздействие электронов на некоторые образцы может привести к неконтролируемым изменениям структуры и состава. Затруднен анализ диэлектриков вследствие зарядки их поверхности электронам. Второй вариант – когда широкорасходящийся первичный пучок характеристического излучения Рассмотрим геометрию возникающей в методе ШРП дифракционной картины с помощью построений в обратном пространстве с привлечением понятия обратной решетки. Следует напомнить, что условие дифракции в терминах ОР имеет вид Пусть угол расходимости первичного пучка характеристического излучения равен p (в пространстве - полусфера). Последовательность построений, необходимых для решения задачи, следующая: 1. Строится ОР монокристалла в трехмерном обратном пространстве в осях 2. Задается направление первичного пучка вектором
Рис. 5.10. Схема возникновения конусов в методе ШРП Для всех узлов ОР, попавших при данных экспериментальных условиях в это пространство, будет выполняться условие дифракции Таким образом, дифракционная картина в методе ШРП представляет собой систему конусов, каждый из которых соответствует определенному отражению (узлу) HKL; оси конусов совпадают с нормалями к отражающим плоскостям (hkl), т.е. с направлением вектора Дифракционная картина, получаемая методом ШРП, достаточно сложна для расшифровки; чаще всего анализируется небольшое число имеющихся на рентгенограмме отражений. Для расчета периода все линии на рентгенограмме проиндицированы, т.е. определены индексы отражений HKL этих линий. При проведении исследований необходимо, чтобы пленка была совершенна по качеству, изотропна и строго перпендикулярна оси пучка, а деформация пленки в процессе обработки минимальна. Метод широко расходящегося пучка применяют для прецизионных (с погрешностью порядка 10-3%) определений периодов решетки монокристаллов, разориентировки элементов, их субструктуры, для изучения структуры кристаллов. Метод порошков (Метод Дебая-Шерера). Дебай и Шеррер получили дифракционную картину, направив пучок характеристического излучения на неподвижный поликристаллический образец. Если кристаллики из котрых состоит образец, достаточно малы (меньше 0,5…2 мкм), то в просвечиваемом объеме (несколько кубических мм) их оказывается миллионы. Следовательно, в образце всегда имеются кристаллики с любой их ориетировкой относительно первичного пучка. Дифракцию в этом случае поясняет построение, приведенное ниже. Рассмотрим условия отражения характеристического излучения с длиной волны λ, от плоскостей (h1k1l1) различных кристалликов образца. Вследствие произвольной ориентировки кристалликов и их большого числа, концы векторов обратной решетки
Ось конуса совпадает с направлением пучка
Другая группа кристалликов, ориентировка которых удовлетворяет условию
дает другой интерференционный конус, основанием которого служит окружность пересечения сферы распространения со сферой радиуса Метод порошков является основным методом исследования технических материалов и широко применяется на практике и позволяет решать обширный круг задач, возникающих при структурном анализе.
5.5. Кинетическая теория рассеяния При выводе интерференционной функции предполагалось, что электроны атома сосредоточены в одной геометрической точки – узле пространственной решетки. При таком условии волны, рассеянные в любом направлении всеми электронами одного атома совпадают по фазе и их амплитуды суммируются. Однако, в действительности, электроны распределены по объему атома, поэтому амплитуды лучей надо складывать геометрически с учетом разности фаз. В результате этого, амплитуда волны, рассеянной атомом, всегда меньше суммы амплитуд волн, рассеянных электронами атома. Отношение амплитуды волны, рассеянной атомом, к амплитуде волны, рассеянной электроном при тех же условиях, называется атомной амплитудой рассеяния рентгеновских лучей. Для корректной оценки получающейся дифракционной картины необходимо учесть влияние многих факторов. Атомный множитель f. Атомный множитель зависит от количества электронов и их расположения в атоме. Если длина волны первичного излучения близка к краю полосы поглощения рассеивающего атома, атомная амплитуда рассеяния становится комплексной величиной.
Структурный множитель F. Интерференционная функция Лауэ выводилась в предположении простой кубической решетки, когда на одну ячейку приходится один атом.
Рис. 5.12. Типы кубической решетки В сложную элементарную ячейку входят несколько атомов, что влияет на получающуюся дифракционную картину. При расчете структурного множителя определяющими параметрами являются две величины: тип элементарной ячейки и рассеивающая способность атома. Величина структурного множителя не зависит от размера элементарной ячейки. Множитель Лоренца L(n) В отличии от идеализированных, реальные кристаллы мозаичны, то есть состоят из блоков малого размера, повернутых друг относительно друга на малые углы (от долей минут до долей градуса). Если блоки достаточно малы и их отклонение от средней ориентировки хаотично, то такой кристалл носит название идеально-мозаичного. Для учета множителя Лоренца, при изучении мозаичных кристаллов используется брэгговский спектрометр.
Рис. 5.13. К определению множителя Лоренца В процессе измерения кристалл медленно поворачивается в небольшом интервале углов около угла дифракции. Вследствие мозаичности кристалла, величина интерференционного максимума не будет строго удовлетворять уравнению Вульфа-Брэггов, так как вклад в отражение дает только некоторая доля блоков мозаики.
Множитель повторяемости P. В методе порошков интенсивность отражения пропорциональна отношению числа кристалликов, участвующих в отражении к общему числу кристалликов.При определении интегральной отражательной способности поликристаллического образца, необходимо принимать во внимание множитель повторяемости, учитывающий число эквивалентных атомных плоскостей, дающих отражение по одному и тому же направлению.Очевидно, что величина Р должна входить только в выражение интегральной интенсивности отражения поликристаллического тела, так как в случае монокристалла условия отражения повторятся при повороте кристалла на 180 градусов.
Температурный множитель exp(-2M)/ Тепловые колебания атомов кристаллической решетки приводят к тому, что центры атомов постоянно смещаются относительно положения равновесия, то есть узлов решетки. Эти смещения даже при комнатной температуре, могут составлять до 10% от межатомных расстояний. Естественно, эти явления приводят к размытию рентгенограммы и ослаблению интенсивности ее линий. Теория дает следующее соотношение для этого эффекта:
где Im – интенсивность без учета тепловых колебаний, Im(T) – истинная интенсивность, а М определяется по формуле (для кубической решетки)
Множитель поглощения A(m, n) Длинноволновое рентгеновское излучение, используемое в рентгеноструктурном анализе, существенно поглощается в исследуемых кристаллах. Учет поглощения различен при исследованиях «на прохождение» и «на отражение».
Рис. 5.14. К учету множителя поглощения Формулы для учета множителя поглощения можно вывести с учетом геометрических условий исследования и формулы ослабления рентгеновского излучения в веществе. В динамической теории рассеяния общая формула интегральной интенсивности имеет вид для монокристаллов:
для поликристаллического образца:
Однако кроме влияния различных множителей необходимо учесть еще некоторые эффекты. Если размеры кристалла достаточно велики и он во всем своем объеме правильный, то допущения, сделанные нами при выводе уравнений Лауэ и Вульфа-Брэггов становятся недопустимыми. Действительно, отношение амплитуды волны, рассеянной одной атомной плоскостью к амплитуде падающей волны имеет порядок 10-5- 10-4. Поэтому, если удовлетворяются условия интерференции и амплитуды рассеянных волн складываются, то уже при числе атомных слоев 103 - 104 амплитуда рассеянной волны становится сравнимой с амплитудой падающей волны. Однако, природные кристаллы минералов и кристаллы металлов и сплавов, как правило, мозаичны Поэтому задачи рентгеноструктурного анализа вполне удовлетворительно решались на основе более простой кинематической теории. Однако давно было обнаружено, что для ряда отражений от крупных природных кристаллов интенсивности, вычисленные по кинематической теория, существенно расходятся с измеренными на опыте. Рассмотрим явление первичной экстинкции. Пусть кристалл находится не в отражающем положении. Тогда первичный пучок, проходя через кристалл, ослабляется, что характеризуется линейным коэффициентом ослабления. Если кристалл находится в отражающем положении то, испытывают повторное отражение. Вторично отраженные лучи отстают по фазе от первичного луча на 180°. Это объясняется тем, что при каждом отражении фаза волны излучения изменяется на 90°. В результате взаимодействия первичной и рассеянной волны происходит ослабление интенсивности пучка.
Рис. 5.15. К выводу первичной экстинкции В мозаичных кристаллах наблюдается вторичная экстинкция, которая также приводит к ослаблению интенсивности первичного пучка, и заключается в экранировании нижних блоков верхними. Пусть кристалл состоит из блоков, слегка разориентированных относительно друг друга. * Рис. 5.15. К выводу вторичной экстинкции Интенсивность первичного пучка, дошедшего до находящегося в отражающем положении блока ослабляется. Величина эффекта зависит от вероятности нахождения на пути луча блоков с одинаковой ориентацией. Разделить вклады обеих экстинкций удается благодаря тому, что зависимость их от угла различна. Измерив интенсивности ряда отражений под разными углами, можно определить вклад той и другой экстинкции. Дата добавления: 2015-12-15 | Просмотры: 2511 | Нарушение авторских прав |

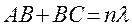 (5.1)
(5.1)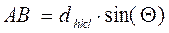 (5.2)
(5.2)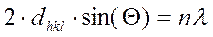 (5.3)
(5.3)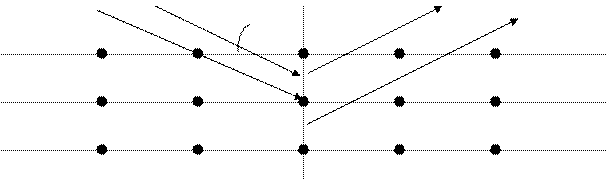
 Q
Q


 a
a (5.4)
(5.4)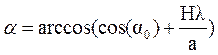 (5.5)
(5.5)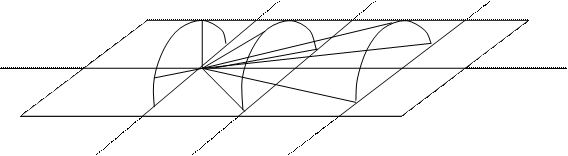
 (5.6)
(5.6)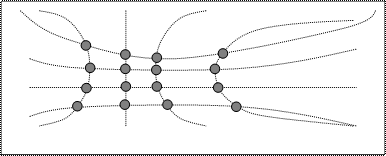
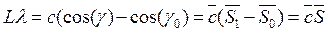 (5.7)
(5.7) (5.9)
(5.9)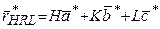 , соединяющей начальный узел 000 с любым другим HKL, перпендикулярен атомной плоскости с индексами Миллера (hkl) в прямой решетке (H = nh, K = nk, L = nl., где n– целое число);
, соединяющей начальный узел 000 с любым другим HKL, перпендикулярен атомной плоскости с индексами Миллера (hkl) в прямой решетке (H = nh, K = nk, L = nl., где n– целое число); (5.10)
(5.10) — межплоскостное расстояние плоскостей (hkl) в прямой решетке.
— межплоскостное расстояние плоскостей (hkl) в прямой решетке.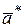 ,
,  ,
,  , связь которых с осями прямой решетки определяется соотношениями
, связь которых с осями прямой решетки определяется соотношениями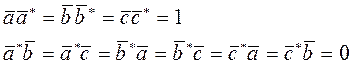 (5.10)
(5.10) , (5.11)
, (5.11)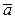 , получаем первое уравнение:
, получаем первое уравнение:  .
.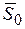 отрезок, численно равный
отрезок, численно равный 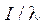 и оканчиваюшийся в узле 0. Очевидно, этот отрезок изображает вектор
и оканчиваюшийся в узле 0. Очевидно, этот отрезок изображает вектор 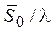 .
.
 . Действительно, из равнобедренного треугольника АОР следует, что в этом случае выполняется уравнение
. Действительно, из равнобедренного треугольника АОР следует, что в этом случае выполняется уравнение . (5.12)
. (5.12) (5.13)
(5.13) , а с другой – сферой радиуса
, а с другой – сферой радиуса 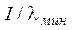 . Все эти сферы в то же время касаются выбранного начального узла 0 обратной решетки, а их центры лежат на направлении первичного луча
. Все эти сферы в то же время касаются выбранного начального узла 0 обратной решетки, а их центры лежат на направлении первичного луча 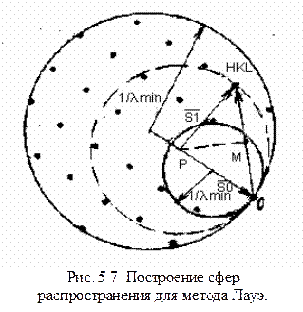
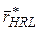 . Из средней по длине вектора
. Из средней по длине вектора 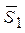 , определяющее положение дифракционного максимума.
, определяющее положение дифракционного максимума. . Используя свойства обратной решетки, получаем, что
. Используя свойства обратной решетки, получаем, что  , а значит, плоскость векторов
, а значит, плоскость векторов 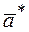 и
и  перпендикулярна оси вращения.
перпендикулярна оси вращения.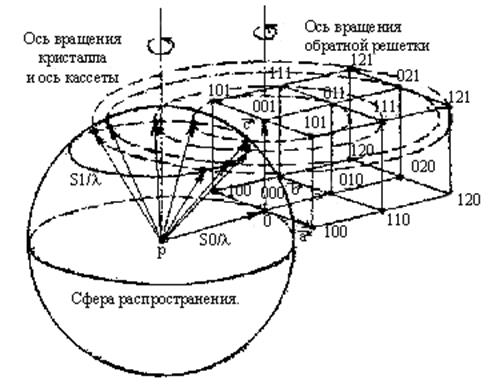
 . Если кристалл вращается, то вместе с ним вращается вокруг параллельной оси обратная решетка. При этом узлы обратной решетки пересекают сферу распространения. В момент пересечения сферы узлом происходит отражение рентгеновских лучей от плоскости кристалла, индексы которой совпадают с индексами этого узла. Видно, что возникающие дифракционные лучи располагаются по образующим конусов, ось которых совпадает с осью вращения кристалла, а основаниями являются окружности пересечения сферы плоскостями обратной решетки. Пересечение конусов с фотопленкой приводит к образованию на ней интерференционных пятен, расположенных вдоль параллельных прямых. Полученные дифракционные отражения используют при определении атомной структуры, размеров элементарной ячейки, числа атомов в одной ячейке.
. Если кристалл вращается, то вместе с ним вращается вокруг параллельной оси обратная решетка. При этом узлы обратной решетки пересекают сферу распространения. В момент пересечения сферы узлом происходит отражение рентгеновских лучей от плоскости кристалла, индексы которой совпадают с индексами этого узла. Видно, что возникающие дифракционные лучи располагаются по образующим конусов, ось которых совпадает с осью вращения кристалла, а основаниями являются окружности пересечения сферы плоскостями обратной решетки. Пересечение конусов с фотопленкой приводит к образованию на ней интерференционных пятен, расположенных вдоль параллельных прямых. Полученные дифракционные отражения используют при определении атомной структуры, размеров элементарной ячейки, числа атомов в одной ячейке. (в электронном микроскопе или рентгеновском микроанализаторе) фокусируется на малом участке поверхности исследуемого монокристалла 1 (рис. 5.9. а, в).
(в электронном микроскопе или рентгеновском микроанализаторе) фокусируется на малом участке поверхности исследуемого монокристалла 1 (рис. 5.9. а, в).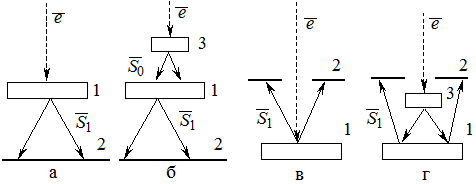
 дифракционные линии называют косселевскими линиями по имени В.Косселя, предложившего данный метод. Достоинством метода ШРП является возможность локального структурного анализа. Степень локальности связана с размером зоны генерации излучения в исследуемом кристалле сечением пучка
дифракционные линии называют косселевскими линиями по имени В.Косселя, предложившего данный метод. Достоинством метода ШРП является возможность локального структурного анализа. Степень локальности связана с размером зоны генерации излучения в исследуемом кристалле сечением пучка 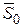 (рис. 5.9. б, г) формируется в рентгеновской трубке при взаимодействии потока
(рис. 5.9. б, г) формируется в рентгеновской трубке при взаимодействии потока  , где
, где 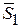 - единичный вектор в направлении дифракции;
- единичный вектор в направлении дифракции;  - единичный вектор в направлении первичного пучка; l - длина волны используемого характеристического излучения;
- единичный вектор в направлении первичного пучка; l - длина волны используемого характеристического излучения;  - радиус-вектор узла ОР с индексами (координатами) HKL. По определению, узел ОР соответствует атомной плоскости (hkl), причем
- радиус-вектор узла ОР с индексами (координатами) HKL. По определению, узел ОР соответствует атомной плоскости (hkl), причем 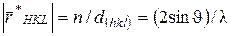 , где n - порядок отражения. Индексы узла HKL связаны с индексами Миллера (hkl): H = nh, K = nk, L = nl.
, где n - порядок отражения. Индексы узла HKL связаны с индексами Миллера (hkl): H = nh, K = nk, L = nl.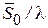 . Конец этого вектора при построении должен обязательно быть в 000. Так как область варьирования направлений
. Конец этого вектора при построении должен обязательно быть в 000. Так как область варьирования направлений 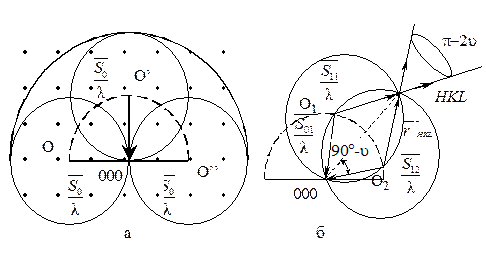
 . Если плоскость фотопленки параллельна отражающей плоскости, т.е. перпендикулярна
. Если плоскость фотопленки параллельна отражающей плоскости, т.е. перпендикулярна  , связанных с различными, кристалликами, образуют сферическую поверхность радиуса
, связанных с различными, кристалликами, образуют сферическую поверхность радиуса 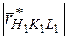 . Эта сферическая поверхность пересекает сферу распространения по окружности, лежащей в плоскости, перпендикулярной первичному пучку. Данная окружность, является основанием конуса, образованного совокупностью лучей, отраженных от плоскостей разных кристалликов образца.
. Эта сферическая поверхность пересекает сферу распространения по окружности, лежащей в плоскости, перпендикулярной первичному пучку. Данная окружность, является основанием конуса, образованного совокупностью лучей, отраженных от плоскостей разных кристалликов образца.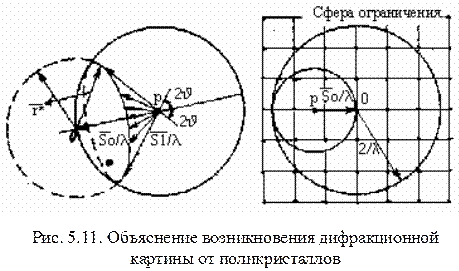
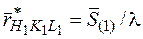 . (5.14)
. (5.14)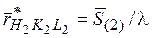 (5.15)
(5.15)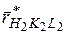 и т.д. Для возникновения отражений от плоскости (hikili) необходимо только, чтобы сфера распространения пересекалась со сферой радиуса
и т.д. Для возникновения отражений от плоскости (hikili) необходимо только, чтобы сфера распространения пересекалась со сферой радиуса  . Сферу радиуса 2/l в обратном пространстве называют сферой ограничения. На рентгенограмме поликристалла могут получиться только те интерференционные линии, которые соответствуют узлам обратной решетки, лежащим внутри сферы ограничения (это положение справедливо и для рефлексов на рентгенограмме вращения).
. Сферу радиуса 2/l в обратном пространстве называют сферой ограничения. На рентгенограмме поликристалла могут получиться только те интерференционные линии, которые соответствуют узлам обратной решетки, лежащим внутри сферы ограничения (это положение справедливо и для рефлексов на рентгенограмме вращения).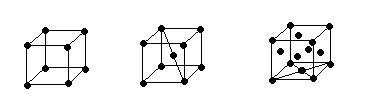
 (5.16)
(5.16)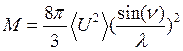 (5.17)
(5.17)
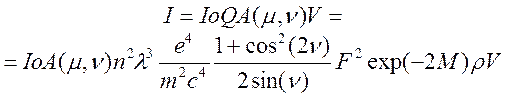 , (5.18)
, (5.18) (5.19)
(5.19)