 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Термосиловой обработкиЗадача данного параграфа заложить основы формальной теории, что достигается определением характерного отклика неупругого материала на изменение напряжения (входной параметр) и деформации (выходной параметр) во времени и наоборот в зависимости от задачи управления. В случае произвольной деформации напряжение и деформация должны быть выражены тензорами второго ранга, и тогда закон Гука превращается в систему линейных уравнений, выражающих каждую компоненту тензора напряжений через компоненту тензора деформации или наоборот. Для нашего случая это обобщение привело бы лишь к ненужному усложнению, поэтому будем исходить из формулировки газона Гука, определяемого соотношениями Известно, что термодинамической системой является любое вещество, которое на ряд бесконечно малых изменений внешнего параметра может проходить через непрерывный ряд равновесных состояний. По этому первому условию неупругости, включающему требования однозначности равновесного соотношения между напряжением и деформацией и вследствие полной восстанавливаем ости, удовлетворяют все материалы, которые подходят под определение термодинамических твердых тел. Второе условие неупругости означает, что в ответ на изменение приложенного механического напряжения для установления равновесия в неупругом материале необходимо время. Самоподнастройка термодинамической системы во времени к новому равновесному состоянию в ответ на изменения входного параметра и будет называться релаксацией. Если в качестве входного воздействия выступает напряжение, неупругая релаксация проявляется как зависимое от времени установление равновесного значения выходного параметра - деформации (или наоборот). Следует отметить, что внешнее проявление релаксации отражает просто подстройку внутренних параметров к новым равновесным значениям. С точки зрения теории автоматического управления внутренние параметры системы будут влиять на количественную сторону переходного процесса, считая релаксацию переходным процессом. Между s и e существует не прямая чисто упругая связь, но также и косвенная связь через внутренний параметр. Таким образом, по мере релаксации внутреннего параметра к равновесному значению, деформация e также стремится к соответствующему значению, с конечной скоростью, а не мгновенно (мгновенное изменение соответствует случаю чистой упругости). Неупругая релаксация является по существу термодинамическим свойством, обусловленным связью s и e с определенными внутренними параметрами, изменение которых к равновесным значениям может происходить в результате кинетических процессов (например, диффузия). Внешним проявлением такой внутренней релаксации являются зависимые от времени деформационные свойства. Как отмечалось ранее, коробление функционально связано с неоднородностью пластического деформирования и температурного поля и, естественно, несовместимостью пластических и упругих деформаций при разгрузке. Аналогичный процесс происходит и с остаточными напряжениями, их релаксация начинается неодновременно по времени и в разных участках изделия как в поперечном, так и продольном сечениях. Разработанные способы стабилизации геометрических форм маложестких деталей основываются на осевой деформации при отпуске (ТСО) с управлением последних при нагреве и охлаждении. Следовательно, целесообразно рассматривать три модели управления: упруго-пластической деформацией, стабилизацией внешних нагрузок и процессом разгрузки. Такое условное разбиение справедливо при рассмотрении стержневой модели, когда анализу подвергаются напряжения первого рода. В первой модели напряжение s(t) и деформация e(t) меняются по времени, управление осуществляется по двум параметрам s и Т°, контролируется выходная величина e(t), во второй s = const, поддерживается САУ постоянной, меняется деформация e, появляется податливость j, в третьей модели напряжение поддерживается постоянным, управление осуществляется по параметру e с учетом изменения температуры Т° остывания. Для количественного исследования процессов прежде всего необходимы уравнения, описывающие ТСО как объект управления, для этого удобно модели разбить на динамические звенья (табл.3.1). Существенно то, что динамическое звено не обязательно является конструктивно или схемно оформленным. В отдельных случаях динамические звенья могут вообще не иметь физического смысла, характеризуя лишь математические зависимости, имеющие место между некоторыми величинами автоматической системы с объектом. Чтобы охарактеризовать состояние динамического звена, примем за обобщенную координату на входе звена s(e), а на выходе e(s) и назовем их соответственно входной и выходной величинами звена направленного действия (однонаправленности).
Таблица 3.1. Динамические звенья и их математическое описание
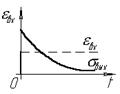
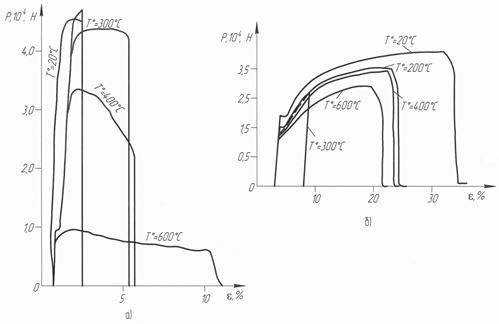
Процесс упруго-пластической деформации можно представить звеном направленного действия с входной величиной s и выходной e и наоборот, в зависимости что исследуется, релаксация напряжений или податливость. Экспериментальная статическая характеристика (зависимость выходной величины e звена от входной s, в установившемся режиме) представлена на рис.3.5. На рисунке (3.5) приведено семейство статических характеристик, построенных для различных постоянных значений температуры Т°. Приведенные статические характеристики не линейны. Для реализации САУ нелинейные характеристики будут линеаризовываться что позволит упростить САУ, не снижая требования к динамике процессов ТСО. Статические характеристики полностью характеризуют поведение динамического звена в установившихся режимах, что позволяет на их основе разрабатывать законы управления упруго-пластической деформацией. Системы управления работают и в неустановившихся режимах, поэтому важной задачей для исследования динамики процесса ТСО является причина поведения динамических звеньев в переходных режимах. В статических характеристиках объекта управления не учитывается время релаксации, что недостаточно для разработки САУ и возможности управления процессом ТСО. Целесообразно перейти к другому описанию на основе системы параметров, которые можно рассматривать как свойства самого материала. Исходной точкой для такого подхода является соотношение между напряжением и деформацией, записанное в виде линейного дифференциального уравнения, включающего напряжение, деформацию и их производные по времени. Далее будет показано, что линейные дифференциальные уравнения деформации, которые описывают неупругость, содержат три независимых параметра. Соответственно модель строится из трех основных элементов - двух пружин и демпфера. Поведение, описываемое уравнением или моделью с тремя параметрами, имеет такое важное значение, что материал, характеризующийся таким поведением, называется стандартным неупругим телом.
Рис.3.5. Экспериментальные статические характеристики объектов управления: а – для стали 40; б – для стали 12Х18Н10Т
Поскольку определение неупругости, приведенное выше, включает требование линейности, ясно, что дифференциальные уравнения неупругости, связывающие s и e, должны быть уравнениями первой степени и содержать столько независимых постоянных, сколько необходимо для описания неупругого поведения данного твердого тела. В общем виде линейное уравнение с постоянными коэффициентами можно записать следующим образом:
Механическая система тогда может служить моделью заданного неупругого материала, когда она подчиняется тем же соотношениям между силой, смещением и временем, которые справедливы для напряжения, деформации и времени в неупругом теле соответственно. Так сила, действующая на пружину, представляет напряжение, смещению-деформацию, а коэффициент жесткости пружины к - соответствует модулю упругости Е или податливости j. Характерная особенность такой пружины: запасенная в ней энергия обратима. Другим элементом, необходимым для обеспечения внутреннего трения, является ньютоновский демпфер, который представляет собой поршень, движущийся в идеально вязкой жидкости, скорость движения поршня пропорциональна действующей силе, следовательно, произведенная полностью работа расходуется на образование тепла. Для описания твердых тел демпфер используется только в комбинации с пружинами. При конструировании моделей механические элементы могут соединяться последовательно и параллельно. При последовательном соединении двух элементов (см. табл.3.1, п.2), напряжения s1 и s2 равны, а деформации складываются. Таким образом
Дата добавления: 2015-01-18 | Просмотры: 741 | Нарушение авторских прав |
 или
или  , где
, где  . Отметим, что при таком подходе предполагается простой способ деформации - чистый сдвиг или одноосная деформация. Неупругость материала можно определить тремя условиями: каждому значению напряжения соответствует единственное равновесное значение деформации и наоборот; равновесное значение выходной величины достигается только по истечении достаточного времени, для достижения равновесия может потребоваться от микросекунд до очень больших промежутков времени; связь между деформацией и напряжением линейна. Первое и третье условия - повторение условий идеальной упругости. Неупругость подразумевает, что кроме мгновенного упругого выходного параметра существует также зависимый от времени неупругий выходной параметр. В данной постановке и задачи смысл линейности охватывает следующее утверждение: если данное изменение во времени напряжения
. Отметим, что при таком подходе предполагается простой способ деформации - чистый сдвиг или одноосная деформация. Неупругость материала можно определить тремя условиями: каждому значению напряжения соответствует единственное равновесное значение деформации и наоборот; равновесное значение выходной величины достигается только по истечении достаточного времени, для достижения равновесия может потребоваться от микросекунд до очень больших промежутков времени; связь между деформацией и напряжением линейна. Первое и третье условия - повторение условий идеальной упругости. Неупругость подразумевает, что кроме мгновенного упругого выходного параметра существует также зависимый от времени неупругий выходной параметр. В данной постановке и задачи смысл линейности охватывает следующее утверждение: если данное изменение во времени напряжения  создает деформацию
создает деформацию  , и если
, и если  вызывает деформацию
вызывает деформацию  , то
, то  приведет к деформации
приведет к деформации 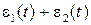 .
.
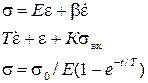


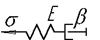






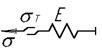
 <
< 

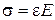




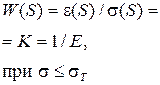





 dе
dе 


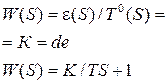

 >
> 


 (3.8)
(3.8)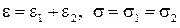 . При параллельном соединении тех же элементов
. При параллельном соединении тех же элементов  . Комбинации моделей различных сочетаний из двух и трех элементов представлены в табл. 3.1.
. Комбинации моделей различных сочетаний из двух и трех элементов представлены в табл. 3.1.