 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Создание динамической модели термосиловой обработки как объекта управленияРанее изложение велось применительно к механическим свойствам металлов при температуре t = 20°С, однако влияние температуры на механические свойства имеет весьма важное практическое значение. Подобно механическим процессам следует различать и температурные эффекты по степени их воздействия: нагрев печи можно отнести к макроэффектам, а температурные при повторных нагрузках к микроэффектам. Ввиду того, что модуль упругости отражает изменение межатомных сил сцепления с изменением межатомных расстояний, естественно ожидать, что модули упругости должны быть связаны с параметрами кристаллических решеток. Уровень температуры существенно влияет на сопротивление пластической деформации (рис.3.6) как видно из рисунка сопротивление начальным пластическим деформациям (предел текучести) существенно зависит от температуры. Следует заметить, что существует принципиальное различие между металлами с решетками ОЦК и ГЦК при изменении температуры. Необходимо иметь в виду, что при деформировании металла при разных температурах следует учитывать также влияние двух факторов: влияние температуры на направление течения при данной структуре деформированного металла и влияние различий в структуре (например, различной плотности дислокаций, возникающих при разных температурах, для материалов с данной степенью деформации. Влияние температуры на кривую деформационного упрочнения металлов с ГЦК решеткой связано с тем, что металл в деформированном состоянии тлеет различную структуру, возникающую при разных температурах и при этом не обнаружено большого изменения напряжения течения с изменением температуры, в то же время физико-химические превращения происходящие при изменении температуры, оказывают на пластичность и вязкость часто сильное влияние. При понижении температуры большей частью сильнее падает пластичность, а не вязкость. Влияние температуры и скорости деформации при ТСО имеют различия, состоящие в том, что упругие характеристики Е, G и не зависят от скорости, но зависят от температуры деформации; изменение температуры (особенно повышение ее) нередко вызывает наложение на чисто механические факторы физико-химических процессов, как происходящих внутри самого металла, так и обусловленных взаимодействием металла с окружающей его средой. Термосиловая обработка, как основная операция технологического процесса, предназначена для выравнивания и минимизации остаточных напряжений по длине заготовки, включает в себя одновременно два процесса, пластического деформирования и температурного воздействия на металл. Если функциональную зависимость напряжение - упругопластическая деформация (рис.3.6) аппроксимировать двумя или несколькими линейными зависимостями, это определяется величиной пластической деформации, то целесообразно для рассмотрения модели процесса нагрева и охлаждения при ТСО обратиться к теории термоупругости и термопластичности. Рассмотрим случай, когда температурное поле предполагается известным и независимым от напряженного состояния, а само тело упругое изотропное. При одноосном нагружении, что соответствует ТСО, закон Гука при тепловых расширениях имеет вид
здесь тепловое расширение складывается с удлинением, обусловленным напряжением. Это же уравнение, выраженное относительно напряжения
Используя принцип сложения действия сил, можно определить температурные смещения и напряжения при нулевых внешних силах, а затем сложить найденные величины со смещениями и напряжениями от действия заданных нагрузок. Температурные напряжения равны нулю, если температура постоянна или является линейной функцией координат (это замечание будет использоваться при разработке алгоритма управления пои ТСО). Сложность математического описания термосиловой обработки, как объекта управления, состоит в том, что исходное распределение температуры, остаточных напряжений, пластических деформаций в объеме заготовки неизвестно или нет измерительных средств, позволяющих контролировать текущее распределение этих параметров. В ходе термосиловых нагружений измеряется температура среды печи и величины упруго-пластических деформаций. Если процесс упруго-пластической деформации начать рано, когда еще не достигнуто желаемое распределение температуры, то ухудшается процесс пластической деформации (большая неравномерность по длине) и время обработки увеличивается. С другой стороны, чересчур длительный нагрев снижает производительность процесса и повышает издержки производства. В настоящий момент, время и скорость нагрева определяют по априорной информации, используя при этом некоторые эвристические правила и приемы. Однако практика показывает, что такое управление процессом недостаточно эффективно, и предлагается система автоматического управления термосиловой обработкой - ТСО в целом.
Рис.3.6. Механическая модель n- го элемента обрабатываемой детали
Для этого необходимо описать сам объект управления, заготовку в термоупругопластическом состоянии. Статическая характеристика объекта управления представлена (рис.3.6) в координатах "сила-перемещение" для сталей 40 и 12X18H10T, из которых следует, что объект ведет себя и как упруго-вязкая, и как упруго-вязкоупрочняющая среда при превышении предела текучести. С учетом разработанных звеньев САУ направленного действия и экспериментов, проводимых на образцах, механическая модель п - го элемента заготовки имеет вид (рис.3.7). Модель тлеет особенность, заключающуюся в том, что для описания перехода от упругой части диаграммы "напряжение - относительное перемещение" к пластической деформации используется пластический элемент (с позиции теории автоматических систем релейный элемент), который дает четкое представление работы механической модели. Если внешнее нагружение не превосходит предела текучести, то paботает верхняя ветвь и стандартное неупругое тело имеет параметры Е 1, Е 2, b1 т.е. в расчетах используется закон Гука, при достижении s02 нагружение идет по второй ветке с параметрами Е 3, Е 4, которые принято называть "переменные модули упругости", "секущие модули" или "модули упрочнения". Для этих же двух зон нагружения представлены в температурные модели, на вход которых подается температура, а на выходе температурные напряжения или просто удлинения, математическое описание этих элементов. Такая механическая модель элемента заготовки позволяет разработать структурную схему объекта управления. Для реализации системы управления ТСО необходима разработка структурной схемы объекта управления. В структурной схеме наглядно реализуется математическая сторона преобразования физических процессов явлений, изменяющихся во времени. Структурные методы в применении к отдельным динамическим элементам позволяют вскрыть их внутреннюю структуру, протекающих в элементах, и позволяют правильно подойти к улучшению характеристик путем наложения дополнительных внешних связей, усиливающих благоприятные или нейтрализующие нежелательные внутренние связи. Применительно к системе в целом структурные методы позволяют установить рациональность системы с точки зрения решения основной возлагаемой на нее задачи по воспроизведению управляющего воздействия при одновременной компенсации действующих на систему возмущений. Детализированная структура непосредственно используется для настройки по ней схемы ЭВМ непрерывного действия, на которой могут быть получены искомые решения. Процесс термодеформации на этапе осевого деформирования, после выхода на заданный температурный режим, описывается уравнениями, согласно статической характеристики и механической модели:
При осевой деформации длинномерных деталейs2 = 0 следовательно, уравнения, описывающее обобщенный закон Гука для плоских сечений, упростятся и передаточные функции объекта управления для одной ветви примут вид:
Здесь Е 1 и Е 2 - модули упругости; b - коэффициент вязкости; Деформация заготовки вдоль осевой оси, одновременно приводит к уменьшению - сужению диаметра заготовки, и следовательно, к упрочнению материала и далее к возрастанию осевых напряжений, т.е. используя терминологию теории автоматического управления, процесс ТСО можно представить как замкнутую систему с положительной обратной связью по напряжению (рис.3.8).
Рис.3.7. Механическая модель n - го элемента обрабатываемой детали
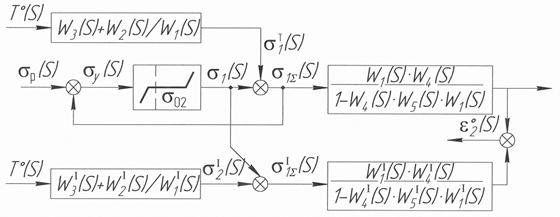
Рис.3.8. Преобразованная структурная схема объекта управления
Входом структурной схемы является осевое напряжение и температура, а выходами продольная и поперечная относительная деформация e1 и e2. Структурная схема согласно статической характеристики объекта имеет две параллельные ветви. При достижении предела текучестиs0,2, в структурной схеме звено представлено как нелинейный элемент типа реле, в работу включается вторая ветвь схемы. Если при одноосном растяжении кривая деформации имеет участок текучести и упрочнения (рис.3.6, а), то нечувствительность "полочки" на кривой показывает, что s Т постоянна, а изменение e в пределах
Рис.3.9. Преобразованная структурная схема п – мерной системы (объекта управления, не связанного регулирования)
На отдельно взятый элемент заготовки, согласно структурной схеме, подается суммарное термодеформационное напряжение При охлаждении заготовки, когда задается периодическая деформация, а напряжение опережает деформацию, тогда
здесь
Смысл величин
здесь С другой стороны, максимальное значение энергии П - запасенной в единице объема определяется выражением
Отношение рассеянной энергии к запасенной, выраженное в процентах, есть удельная демпфирующая способность материала. Естественно, что это отношение связано с углом потерь
Аналогично это отношение выразится и через модуль
Дата добавления: 2015-01-18 | Просмотры: 733 | Нарушение авторских прав |
 , (3.9)
, (3.9) . (3.10)
. (3.10)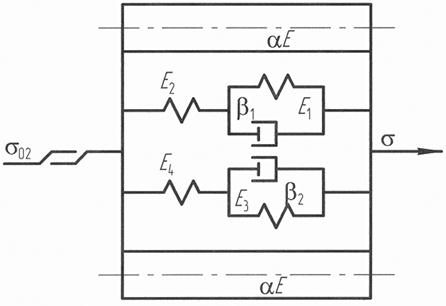
 (3.11)
(3.11) (3.12)
(3.12)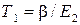 ,
, 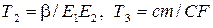 - постоянные времени; к 1 … к 5 - коэффициенты усиления; С - удельная теплоемкость; F - поверхность заготовки; c Т - удельный коэффициент теплоотдачи; m - коэффициент Пуассона.
- постоянные времени; к 1 … к 5 - коэффициенты усиления; С - удельная теплоемкость; F - поверхность заготовки; c Т - удельный коэффициент теплоотдачи; m - коэффициент Пуассона.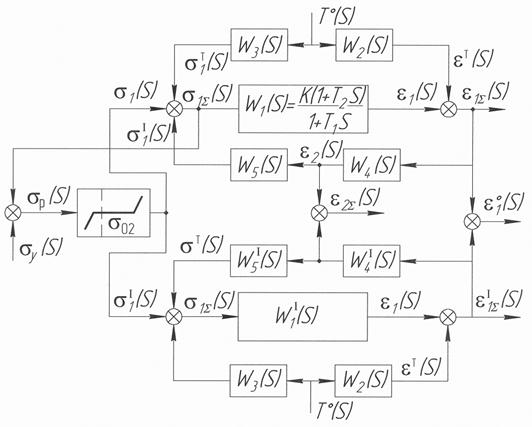
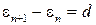 , то
, то 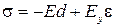 при e ≥ e а, где e а, - деформация при постоянном напряжении. Для разных материалов величина "полочки" разная. Если есть ограничение (насыщение) предел текучести не меняется и нет кривой упрочнения, то
при e ≥ e а, где e а, - деформация при постоянном напряжении. Для разных материалов величина "полочки" разная. Если есть ограничение (насыщение) предел текучести не меняется и нет кривой упрочнения, то  , при
, при  , при
, при 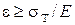 . Учет перехода с одной ветви структуры на другую, т.е. при переходе через предел текучести, на первой ветви введена единичная обратная связь, которая включает "реле" и процесс осевой деформации идет по второй ветви. Процесс упрочнения (кривую упрочнения) целесообразно линеаризировать, что справедливо при малых величинах деформации, тогда и передаточная функция по своей сути остается такой же, что и предыдущая, только изменяются численные значения постоянных времени и коэффициентов усиления (передаточная функция обозначена штрихом W I(S) рис.3.9).
. Учет перехода с одной ветви структуры на другую, т.е. при переходе через предел текучести, на первой ветви введена единичная обратная связь, которая включает "реле" и процесс осевой деформации идет по второй ветви. Процесс упрочнения (кривую упрочнения) целесообразно линеаризировать, что справедливо при малых величинах деформации, тогда и передаточная функция по своей сути остается такой же, что и предыдущая, только изменяются численные значения постоянных времени и коэффициентов усиления (передаточная функция обозначена штрихом W I(S) рис.3.9).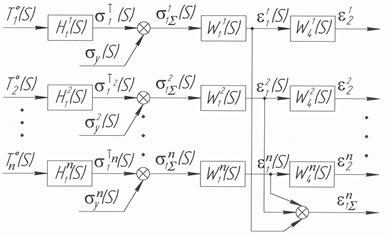
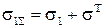 . На выходе каждой ветви структуры величина относительного удлинения равна также сумме деформаций
. На выходе каждой ветви структуры величина относительного удлинения равна также сумме деформаций 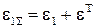 ,
,  . Полная относительная деформация в продольном и поперечном направлении равна
. Полная относительная деформация в продольном и поперечном направлении равна  . После структурных преобразований объект управления представлен на рис.3.9. Принцип управления обработкой длинномерных маложестких деталей принят модальным для процесса правки и мехобработке, приемлем он и для процесса термодеформаций, т.к. деформация e1 является интегральным показателем и в этом случае теряется информация по длине детали. Контроль за поперечной деформацией e2 позволяет более точно оценить процесс осевого нагружения по всей длине и обеспечить равномерное сужение-деформацию вала; без локализации какой-то одной "шейки". Объект управления в этом случае целесообразно представить структурной схемой n - мерной системы несвязанного регулирования. Внутренняя связь между элементами (частями заготовки) существует, но для каждого контура управления она будет являться внешней нагрузкой в виде силового или теплового потоков. Структурная схема рис. 2.1 получена на основе разработки п - го элемента рис.3.8. После несложных преобразований и упрощений таких, как свертывание передаточных функций
. После структурных преобразований объект управления представлен на рис.3.9. Принцип управления обработкой длинномерных маложестких деталей принят модальным для процесса правки и мехобработке, приемлем он и для процесса термодеформаций, т.к. деформация e1 является интегральным показателем и в этом случае теряется информация по длине детали. Контроль за поперечной деформацией e2 позволяет более точно оценить процесс осевого нагружения по всей длине и обеспечить равномерное сужение-деформацию вала; без локализации какой-то одной "шейки". Объект управления в этом случае целесообразно представить структурной схемой n - мерной системы несвязанного регулирования. Внутренняя связь между элементами (частями заготовки) существует, но для каждого контура управления она будет являться внешней нагрузкой в виде силового или теплового потоков. Структурная схема рис. 2.1 получена на основе разработки п - го элемента рис.3.8. После несложных преобразований и упрощений таких, как свертывание передаточных функций 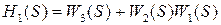 и отказ от нелинейного элемента, работа которого определяется самой САУ. Упрощение не изменяет физики процесса термодеформации с осевым нагружением. Здесь следует заметить, что для получения информации о поведении материала заготовки за короткое время удобны динамические оценки (например, вибрационные воздействия). При этом на изделие накладывается периодически изменяющиеся во времени напряжения (или деформация) и определяется отставание по фазе деформации от напряжения и наоборот. Так, при нагружении, заготовки осевой силой передаточная функция, связывающая выход с входом рассматриваемого звена
и отказ от нелинейного элемента, работа которого определяется самой САУ. Упрощение не изменяет физики процесса термодеформации с осевым нагружением. Здесь следует заметить, что для получения информации о поведении материала заготовки за короткое время удобны динамические оценки (например, вибрационные воздействия). При этом на изделие накладывается периодически изменяющиеся во времени напряжения (или деформация) и определяется отставание по фазе деформации от напряжения и наоборот. Так, при нагружении, заготовки осевой силой передаточная функция, связывающая выход с входом рассматриваемого звена  , где
, где  - действительная часть (податливость накопления);
- действительная часть (податливость накопления);  - мнимая часть (податливость потерь). Представляя
- мнимая часть (податливость потерь). Представляя 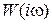 как вектор, который характеризует установившееся движение при периодическом возмущении с частотой w (в пределах от 0 до ¥), получим АФЧХ на комплексной плоскости, что дает проследить как связаны
как вектор, который характеризует установившееся движение при периодическом возмущении с частотой w (в пределах от 0 до ¥), получим АФЧХ на комплексной плоскости, что дает проследить как связаны 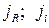 и Ф;
и Ф; 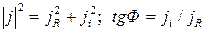 , здесь Ф - величина внутреннего трения материала.
, здесь Ф - величина внутреннего трения материала.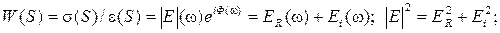
 ,
,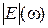 - абсолютный динамический модуль упругости в комплексной форме, то
- абсолютный динамический модуль упругости в комплексной форме, то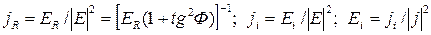 .
. и
и 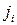 как "податливости накопления" и "податливости потерь" соответственно иллюстрируется вычислением энергии, запасенной и рассеянной за период колебаний, это важно, когда в процессе термодеформации используется виброобработка как процесс, ускоряющий, релаксацию. Энергия в единице объема в любой момент времени в течение цикла равна
как "податливости накопления" и "податливости потерь" соответственно иллюстрируется вычислением энергии, запасенной и рассеянной за период колебаний, это важно, когда в процессе термодеформации используется виброобработка как процесс, ускоряющий, релаксацию. Энергия в единице объема в любой момент времени в течение цикла равна 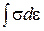 , где интегрирование производится между начальной и рассматриваемой точками цикла. Энергия П ц, рассеяна на весь цикл в единице объема, равна
, где интегрирование производится между начальной и рассматриваемой точками цикла. Энергия П ц, рассеяна на весь цикл в единице объема, равна , (3.13)
, (3.13) - амплитуда напряжений.
- амплитуда напряжений.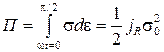 . (3.14)
. (3.14)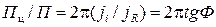 . (3.15)
. (3.15)
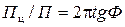 . Поскольку Ф (или tg Ф) является мерой потерь энергии (за один период), обусловленных неупругим поведением.
. Поскольку Ф (или tg Ф) является мерой потерь энергии (за один период), обусловленных неупругим поведением.