 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Управления процессом термосиловой обработкиПрежде чем рассматривать разработанную САУ термосиловой обработки (ТСО), следует сделать замечание по физике процесса. В настоящее время не представляется возможным описать уравнениями состояния реономного тела, как бы тщательно оно не было изучено. Применение макроскопического реономенологического подхода, при котором не учитываются детальные устройства системы и работа отдельных элементов, а изучается функционирование системы в целом, как связь между выходом и входом, такие не решает поставленную задачу. Процесс пластической деформации имеет ряд особенностей. Одна из них это зависимость сопротивления деформации в данный момент времени от истории деформации - технологической наследственности, т.е. от закона развития деформации во времени. Сопротивление пластической деформации нельзя задать в виде Из определения остаточных напряжений не ясно, какие же причины лежат в основе образования поля остаточных напряжений. Единственное, что можно выяснить, что способ их определения, известный как теоремы о разгрузке. В чем сущность возникновения и развития остаточных напряжений? Для пояснениях их происхождения рассмотрим графическую интерпретацию образования остаточных напряжений с помощью схематизированной кривой Рассмотрим наиболее характерных три варианта несовместимости деформаций при разгрузке, первый - модули упругости При первом варианте, когда модули упругости стержней не равны между собой, как и их модули упрочнения (рис.3.10, б) целесообразно сравнить два стержня 1 и 2, это не нарушит понимание физики процесса и упростит рисунок. Рассмотрим два варианта разгрузки, стержень 2 находится при нагрузке еще в упругом состоянии и его деформация по закону Гука После разгрузки величина деформации в стержне 1 равно
Рис.3.10. Стержневая плоская модель деталей типа вал (а) и диаграммы нагружения (разгрузки) с неравными модулями упругости и упрочнения (б); нагружения стержней с разными пластическими деформациями (в); нагружения стержней в различных состояниях при нагрузке (г): 1', 2', 3' – характеристики стержней 1, 2, 3 соответственно
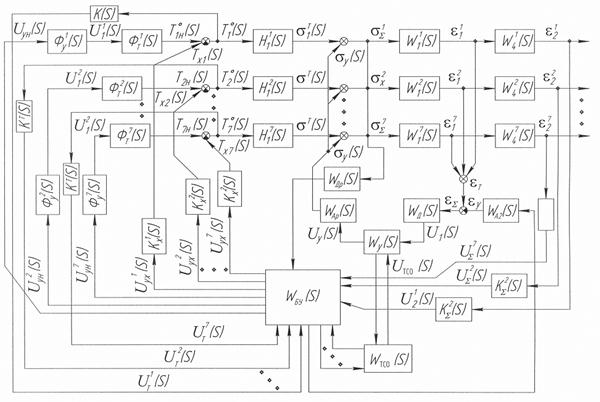
Деформация сжатия стержней будет идти до тех пор, пока не наступит упругое равновесие Из приведенного примера видно, что различие в механических свойствах наружных и внутренних частей изделия (вала) приводит к тому, что при разгрузке не вся накопленная системой потенциальная энергия рассеивается, причем, чем больше величина пластической деформации, тем больше накапливается энергии. Если тело до деформации имело однородные свойства в сечении, а при деформации, в процессе нагружения три соседних элемента 1 … 3 получили различные пластические деформации, то при одной и той же полной деформации элементы достигли предела упругости Третий вариант - все три стержня имеют одинаковый модуль упругости, но температура 1 и 3 элемента (поверхности вала) повышается настолько, что их пределы текучести заметно меньше предела текучести 2 стержня (рис.3.10, г). Здесь и в предыдущих случаях различные пластические деформации приводят к появлению остаточных напряжений. Следует отметить, что во всех рассмотренных случаях остаточные наполнения исчезают, если элементы системы (стержни) освободить от связи одного с другим (например, проточить на токарном станке). Тогда система без связей свободно рассеивает накопленную потенциальную энергию, хотя следует заметить, что геометрия таких свободных элементов будет другой, т.е. нарушается совместность пластических деформаций. В процессе разгрузки действительное перемещение в координатах Если в качестве внешнего воздействия выступает разновременность газовых превращений различных окрестностей деформируемого тела, то можно построить диаграммы подобные как на рис.3.10, т.к. базовые изменения в общем случае вызывают изменения объема и механических характеристик в различных точках тела в различное время. Такое же физическое толкование справедливо и для микронапряжений второго рода. Можно считать, что непосредственной причиной развития остаточных напряжений является несовместность пластических деформаций, возникающих при нагружении изделия любым видом воздействия. С этих позиций следует рассмотреть механизм возникновения остаточных напряжений в круглом прокате при горячей прокатке. При прокате круглого профиля можно выделить две причины возникновения и развития остаточных напряжений: неравномерность пластических деформаций металла при обжатии, результат механического воздействия и неоднородность температурного поля, возникающего в процессе прокатки и охлаждения. Прокат для изготовления длинномерных деталей типа "вал" имеет прогиб в силу перечисленных причин, и технология его изготовления требует таких технологических приемов, которые позволяли бы стабилизировать и минимизировать уровень остаточных напряжений в сечениях готовых изделий. На первом этапе проектирования, когда идет изучение объекта и возможности САУ в целом, целесообразно использовать по возможности упрощенную модель, учитывая лишь основные связи. Такой подход позволяет физически просто осмыслить полученные результаты и накопить опыт проектирования САУ в рамках линейной теории. Степень идеализации САУ нельзя рассматривать в отрыве от тех задач, которые она должна решать и тех требований, которые к ней предъявляются. Применительно к задачам ТСО САУ представляет собой соединение различных многомерных звеньев и здесь в понятие объекта управления включается кроме математической модели собственно объекта управления и заданные динамические характеристики усилительно-регулирующих и измерительных устройств. Кроме того, на сам объект при ТСО наложены связи, одна связь обусловлена физическими свойствами регулируемого объекта, как увеличение температуры приводит к уменьшению прочностных характеристик обрабатываемого материала, с ростом внесшего рабочего усилия растет продольная и поперечная деформация. Второй ряд связей накладывается на систему управления по условиям, определяющимися технологическим процессом (внешние связи). Кроме того, сложность разработки САУ процессом нагрева заготовки, как объекта управления с входными и выходивши параметрами, состоит в том, что исходное распределение температуры в заготовке неизвестно и нет измерительных средств, позволяющих контролировать текущее распределение. В ходе процесса нагрева измеряется лишь температура рабочей среды печи. Такая неполнота измерительной информации о ходе процесса затрудняет регулирование скорости нагрева и определение момента стабилизации температуры по длине и диаметру заготовки. Как отмечалось ранее, целью разработки САУ ТСО является создание равновесного минимального напряженного состояния заготовки в поперечном и продольном сечениях. Прямого контроля за реономным поведением материала во времени и процессе ТСО осуществить невозможно и поэтому в разработанной САУ были применены косвенные методы измерения в реальном масштабе времени таких параметров, как удлинение и сужение заготовки, внешнее усилие, приложенное к ней, температура нагрева и охлаждения, а также их производных. На основании априорной информации о взаимодействии перечисленных параметров и математических зависимостях, была разработана многоканальная, с автономными каналами, система управления, работающая по составленным алгоритмам, отдельные контуры которой работают как следящие системы по отклонению регулируемого параметра (пример, управление за поперечной деформацией изделия) и как системы стабилизации - внешнего усилия с заданной величиной деформации (управление продольной деформацией и температурой нагрева и охлаждения). Структурная схема ТСО (рис.3.11) включает в себя сам объект управления – семь автономных каналов с передаточными функциями
Количество каналов определяется согласно модальному принципу управления, применение которого подробно доказано на примере САУ механической обработки. Технологический процесс обработки маложестких длинномерных деталей построен на всех операциях правки, термосиловой обработки, мехобработки и виброобработки на модальном принципе, т.е. управляющее воздействие прикладывается в зонах и узлах пучности первых трех гармоник и в этих же зонах контролируются деформации, т.е. семь модулей для правки и мехобработки. Соответственно и термосиловая обработка построена по тому же принципу - семиканальной системы управления. Все каналы идентичны и каждый имеет по два выхода и входа. Контролируемые параметры на выходе Следует отметить, что этот контур обеспечивает управление осевой деформации, которая является интегральным параметром, т.к. в процессе ТСО невозможно проконтролировать осевую деформацию по длине заготовки на отдельном участке вала, в силу отсутствия технических средств измерения. Поперечная деформация, связанная с продольной через коэффициент Пауссона, несет больше информации о техпроцессе и легко поддается контролю в любой точке заготовки с большей точностью. Контур контроля и управления за поперечной деформацией по длине изделия, с учетом количества каналов, включает в себя следующие звенья: первичный преобразователь
Рис.3.11. Структурная схема управления ТСО
Каждый из каналов нагрева и охлаждения имеет контур обратной связи, в который включено одно звено (термопара) с передаточной функцией Кроме каналов нагрева печи, система управления имеет столько же каналов быстрого охлаждения, на рис.3.11 каналы представлены одним звеном Разработанная структурная схема аналогична схемам для мехобработки и правки, имеет идентичные каналы управления, с теми же элементами контроля, управления и исполнительными механизмами, кроме источников нагрева. Последние выбраны стандартными и никаких особенностей в динамике и статике управления не имеют. Быстродействие электронных блоков на несколько порядков выше самого процесса ТСО и исследовать динамику поведения контуров управления не имеет смысла, (экспериментальные исследования подтвердили эти предпосылки). Расчет на управляемость, устойчивость и точность для семиканальных автономных контуров управления САУ ТСО аналогичен расчету, проведенному для САУ механической обработки. Рассмотрим влияние обратной связи, САУ на объект управления. Для наглядности упростим схему, представив объект одной передаточной функцией
Рис.3.11.1. Упрощенная структурная схема управления ТСО (а) и статическая характеристика объекта с обратной связью
Здесь характеристика объекта без обратной связи - кривая I, а с контуром управления - кривая II. В случае отрицательной обратной связи Целесообразно остановиться на технологических проблемах, связанных с управлением ТСО (отпуск, нормализация и т.д.) с учетом прочностных характеристик и физмехсвойств обрабатываемого материала. Известные работы в области управления уровнем остаточных напряжений решают задачу расчета, на основе априорной информации о времени, о времени охлаждения изделия на последней стадии его проката, с целью выравнивания температур по сечению изделия из минимизации таким образом уровня остаточных напряжений. Задача управления в этом случае сводится к созданию совместных пластических деформаций. В первой главе подробно разбирались причины коробления маложестких деталей, здесь только заметим, что потеря геометрической точности изделия напрямую связана с возникновением остаточных напряжений первого рода, последние возникаю из-за неравномерности пластических деформаций металла, неоднородности температурного поля профиля заготовки в процессе охлаждения, разновременности протекания процесса структурных превращений. Для минимизации уровня остаточных напряжений необходимо устранить, свести к нулю выше перечисленные причины возникновения остаточных напряжений, для этого необходимо управлять текущими параметрами процесса ТСО. Трудность в выборе управляемых параметров состоит в том, что нет однозначных зависимостей между текущими и конечными параметрами в процессе ТСО. За основные (доминирующие), параметры управления были приняты - температура и продольная деформация. Процесс термосиловой обработки необходимо разбить на три этапа - нагрузки, выстоя и разгрузки. Каждый из этапов требует своего технологического приема, в зависимости от прочностных характеристик металла. Так, существует стандартная технология таких операций, как отпуск и т.д., температурный режим таких операций известен, но как правило, этот режим назначается из задач металловедения, а не технологии обработки МЖД, связанных с короблением. Снижение уровня остаточных напряжений, как правило, приводит к короблению деталей в процессе отпуска или отжига, а дальнейшее исправление криволинейности вводит свои неоднородные остаточные напряжения и т.д. Целью данной ТСО является минимизация и стабилизация остаточных напряжений в продольном и поперечном направлениях длинномерной детали. Для достижения данной цели необходимо решить один из главных вопросов, при какой температуре проводить термосиловую обработку. На рис. 3.5 приведены зависимости предела текучести от температуры для различных конструкционных сталей, построенных по данным таблиц механических свойств при повышенных температурах. Для конструкционных сталей характерно наличие участков со слабой зависимостью предела текучести от температуры, причем такие участки лежат в интервале (0,15 … 0,25)
Рис.3.12. Экспериментальные зависимости σ02 от температуры для конструкционных сталей
Для изделий из таких сталей требуется особо тщательно выбирать ту величину пластической деформации, на которую скачкообразно и локально деформируются микрообъемы металла при выходе за предел упругости - критическая деформация для различных материалов разная, но не превышает 4 %. При переходе за предел текучести одновременного охвата пластической деформацией всего объема металла не происходит до тех пор, пока все микрообъемы металла не окажутся охваченными пластической деформацией критической величины. Только после этого возможна одновременная деформация всего объема материала. Трудность определения этой критической величины, как информации для задатчика блока управления осевой деформации заключается в том, что эта величина зависит от размера зерна, термической обработки, скорости деформирования и т.д. Следовательно, контроль за неравномерностью пластической деформации по длине изделия необходим. Как и необходим критерий, характеризующий среднюю неравномерность пластических деформаций Значение
Рис.3.13. Зависимость Кср от средней остаточной деформации εср для стали марки 12Х18Н10Т
Неравномерность пластической деформации в микрообъемах оказывает значительное влияние на процесс пластического течения в целом и на критерии прочности, однако количественного влияния микронеоднородности на макронеоднородность пластической деформации пока еще сделать не удается. Неравномерность пластической деформации имеет две фазы протекания. Первая - одновременная, но неравномерная деформация микрообъема металла тлеет решающее значение для оценки неоднородности пластических свойств материалов. Критерий Устойчивость хода равномерного пластического течения происходит путем перемещения очага деформации по длине растягиваемого образца, от более упрочненного участка к менее упрочненному. Процесс равномерной деформации справедлив при условии В процессе температурно-силового нагружения происходят изменения напряжений и второго рода, на которых следует остановиться. Основные внешние напряжения ускоряют релаксацию напряжений второго рода, но их главная роль состоит в выравнивании напряжений первого рода, т.е. в стабилизации формы вала. Заметим, что осевые нагрузки можно сочетать также и с вибрационным методом. Этот вопрос будет рассмотрен отдельно. Сложностью в реализации разработанной технологии ТСО является сам объект управления - обрабатываемая деталь, ее математическая модель. Здесь необходимо решить проблему контроля и управления структурной перестройки материала заготовки, т.к. упрочнение кристаллических материалов в результате холодной обработки - наклеп, возрастает из-за увеличения плотности дислокаций. При этом образуются сетки дислокаций, перемещение данной дислокации в плоскости, пронизанной другими дислокациями, затруднено. Оценка сил, действующих на головную дислокацию в стенке, показывает, что возникают напряжения выше предела упругости,
где: При нагревании, когда температура достигает такой величины, при которой становятся существенными процессы диффузии, частицы мелкодисперсной фазы начинают растворяться, и при обмене растворенных атомов вследствие диффузии - перемещаться вместе с дислокациями. Переползание дислокаций и отжиг ведут к уменьшению плотности дислокаций. В результате неоднородной пластической деформации поверхностного наклепа образуются остаточные напряжения. Наружные слои сжимаются, а внутренние слои растягиваются. Поскольку наружный слой имеет обычно малую толщину, напряжения сжатия в нем значительно превышают растягивающие напряжения во внутренних слоях. В абсолютной величине радиальные напряжения в 8 … 10 раз меньше, чем осевые остаточные напряжения. Задачей ТСО является повышение однородности свойств заготовки, т.е. уменьшение разброса значений касательных Чтобы вызвать диффузию неоднородностей предлагается приложить внешние растягивающие осевые силы и одновременно провести нагрев заготовки в печи. Растягивающее внешнее напряжение уменьшает внутренние сжимающие напряжения, что сопровождается диффузией дефектов и структурной перестройкой. Повышение температуры понижает напряжение пластической деформации. Кроме того за счет неравномерного нагрева (наружный слой прогревается быстро, а середина остается холодной) создаются термонапряжения, которые нарушают равновесие между концентрационными и упругими напряжениями, что увеличивает диффузию дефектов. Эмпирическая зависимость коэффициента диффузии от температуры имеет следующий вид
здесь R зер - размер зерен. При этом диффузия происходит по границам зерен. Неоднородность в распределении напряжений связана с различием в размерах зерен, разной пластической деформацией и их взаимной ориентации. Описать измерение всех факторов очень сложно. Для простоты будем считать, что неоднородность обусловлена различными углами разориентировки межзеренных границ. Энергия дислокационной границы описывается формулой
где Покажем, что внешние осевые напряжения оказывают ориентирующие действия на текстуру заготовки (детали), что в конечном счете уменьшает неоднородность напряжений. Если кристаллы обладают анизотропией, то их энергию в зависимости от ориентации зерна по отношению к внешнему напряжению можно записать
где
Из условия устойчивости Структурная перестройка, проходящая в поверхностном слое сопровождается выделением энергии, запасенной за счет пластической деформации. Эту энергию в форме звуковых колебаний можно зафиксировать непосредственно с помощью пьезопреобразователя, укрепленного на поверхности детали. Пусть за счет неоднородностей существует распределение напряжений по некоторому закону, например, по нормальному закону
со средним Пусть к валу приложено внешнее растягивающее напряжение Относительное число таких зерен, и следовательно, интенсивность сигнала
где Так как Анализ математической модели показывает, что приложение растягивающих напряжений приводит к уменьшению неоднородности в распределении остаточных напряжений. Регистрацию и управление перестройки структуры материала целесообразно осуществлять по выделению энергии высокочастотных колебаний сопровождающих эту перестройку. При воздействии осевых напряжений, равных или превышающих предел текучести, устанавливается структура, которую характеризует большая степень однородности и преимущественная ориентация зерен вдоль оси. Объяснить это можно тем, что за счет движения дислокации уменьшаются углы разориентировки границ. Так как угол разориентировки границ связан с концентрацией дислокаций в границах, то основным механизмом будет движение дислокаций. Размножение и скольжение дислокаций объясняется моделью Франка и Рида. Согласно этой модели могут генерироваться дислокационные петли, если напряжение
где Наиболее непосредственный механизм торможения дислокации - существование в кристаллите частиц другой фазы. При обработке аустенитной стали такой фазой будут дисперсные частицы мартенситной фазы. Большую роль в закреплении дислокаций играют также растворенные атомы. Таким образом, чем больше наклеп, тем менее подвижны дислокации. При достаточно большом осевом напряжении внутри зерен возникает генерация дислокации. Так как дислокации внутри зерна имеют знак, противоположный знаку дислокаций в границах, то угол разориентировки границ уменьшается. При этом концентрация дислокаций внутри зерна может практически не меняться, т.е. наклеп и прочность не изменяются. Такое утверждение справедливо для зерен, у которых меньший наклеп и угол Если
где h - коэффициент сдвиговой вязкости; Релаксация напряжений определяется уравнением Релаксация напряжений второго рода вызывает релаксацию напряжений первого рода. Связь здесь достаточно сложная и можно говорить об оценочных формулах. Примем, что изменение напряжений описывается кинетическим уравнением, аналогичным известным уравнениям теплопроводности и диффузии. Тогда второе уравнение Фика имеет вид
где
В одномерном случае для границы между двумя блоками зерен, которые имеют различные наполнения, отличающиеся на
Здесь
Выражение для Целесообразно использовать циклический режим осевой нагрузки зала. При повторном нагружении пластически деформированного образца его сопротивление пластическим деформациям стекается. Это связано со структурной перестройкой и релаксацией напряжений. Поэтому циклическую нагрузку можно использовать одновременно как метод контроля. Низкотемпературная силовая обработка дает возможность снизить критическое напряжение, необходимое для релаксации напряжений второго рода. Скольжение дислокаций зависит в конечном счете от подвижных точечных дефектов и растворенных атомов примеси, а также от концентрации метастабильной фазы (в нашем случае частиц мартенсита), которые являются стопорами для дислокаций. Следовательно, если нагревать деталь до температуры порядка 300°С, то в соответствии с (3.25) уменьшается время релаксации напряжений второго рода и, соответственно время релаксации напряжений первого рода. Второй этап ТСО - выдержка (выстой) при постоянной температуре и вибрационном воздействии с целью минимизации времени релаксации и уровня остаточных напряжений. При этом стабилизируется осевая деформация, внешняя нагрузка и температура по длине и сечению изделия. Вибрационное воздействие на деталь с целью получить равномерное распределение напряжений, т.е. вызвать быстрое "старение" детали, имеет ряд преимуществ по сравнению с другими способами создания устойчивой формы. Использование резонансного поглощения энергии, с одной стороны, дает возможность концентрированного поглощения энергии дефектами и различными неоднородностями, а с другой, как будет показано ниже, может быть использовано как сигнал управления процессом. Независимо от физической природы поглощения энергии внешнее проявление его в материале или конструкции наблюдается в виде петли гистерезиса, образующейся при вынужденных колебаниях. Форма петли зависит от многих факторов, но достаточно ограничиться определением ее площади, так как именно площадь петли гистерезиса характеризует энергию, рассеянную в материале, которая ограничивает величину амплитуды резонансных колебаний. Логарифмический декремент затухания можно определить экспериментально по известной формуле, Очевидно, что вибрационное воздействие может привести к структурной перестройке, т.е. к изменению напряжений первого рода в области пластичности; в этой области поглощение будет максимальным. Необходимый рабочий режим создается за счет внешнего растягивающего напряжения. Для определения параметров петли необходимо исследовать колебания системы с одной степенью свободы при однородном распределении напряжений по объему упругого элемента.
где Рассмотрим явление резонанса и зависимость логарифмического декремента от свойств материала и параметров внешнего воздействия Решение (3.30) дает значение амплитуды
Энергия и плотность энергии при резонансе
Здесь Установлено, что неупругие смещения создаются за счет генерации и перемещения дислокаций. Источником дислокаций могут быть сидячие или заторможенные дислокации, которые генерируют при достаточно больших напряжениях Если образуется дислокационная петля, то изменение энергии определяется зависимостью
где Из (3.33) энергия хаотического движения, приходящаяся на дислокационную петлю
где "Время жизни", т.е. частота испускания дислокационных петель определяется по формуле Больцмана
Очевидно, что коэффициент затухания
Заметим, что если
где Окончательно получим трансцендентное уравнение, определяющее зависимость
где На рисунке приведены зависимости Вибрационное воздействие вызывает перемещение дислокаций и связанных с ними напряжений второго рода в области нагрузок, меньших предела упругости. Так как перераспределение напряжений связано с резким усилением поглощения колебаний, то виброакустический сигнал можно использовать не только как внешнее воздействие, но и как диагностический признак. Обычно для конструкционных сталей существенное понижение прочностных характеристик, нежелательное для эксплуатации, происходит после нагрева до Т ° = 330…350 ° С, т.е. выше значения Цель рассмотренных двух этапов ТСО устранение технологической наследственности (стабилизация и минимизация остаточных напряжений в сечении и по длине заготовки). Если материал изделия имеет площадку текучести на диаграмме В процессе термосиловой обработки ТСО с применением САУ, когда температура нагрева заготовки не превышает температуру отпуска, целесообразно сформировать остаточные напряжения одного знака в поперечном сечении и снизить их уровень, при этом выровнять мехсвойства материала по длине заготовки, как было описано выше. На третьем этапе ТСО разгрузке, могут появиться новые остаточные напряжения за счет несовместимости упругих и пластических деформаций. Пределы текучести с понижением температуры резко возрастают, особенно в интервалах Т = (250 … 20)°С, а следовательно, единственно приемлемым технологическим приемом является автоматическое управление термосиловой разгрузкой, когда контролируется и управляется внешняя нагрузка, возникающая при охлаждении изделия и скорость охлаждения. Алгоритмы разгрузки и их реализация.
Дата добавления: 2015-01-18 | Просмотры: 801 | Нарушение авторских прав |
 , т.е. как функцию от степени деформации при данной фиксированной температуре. Если достичь заданного
, т.е. как функцию от степени деформации при данной фиксированной температуре. Если достичь заданного  и далее обеспечить
и далее обеспечить  , то напряжение будет уменьшаться, хотя степень деформации останется неизменной. Это свидетельствует о том, что единой формулы типа
, то напряжение будет уменьшаться, хотя степень деформации останется неизменной. Это свидетельствует о том, что единой формулы типа  не существует. Приведенные ранее уравнения моделей неупругих тел и их решения показывают, что напряжение
не существует. Приведенные ранее уравнения моделей неупругих тел и их решения показывают, что напряжение  не определяется значением
не определяется значением  в данный момент времени, а зависит от функции
в данный момент времени, а зависит от функции  . Допущение, что время релаксации постоянно для материалов, не соответствует экспериментальным данным. Нельзя считать известной функцию
. Допущение, что время релаксации постоянно для материалов, не соответствует экспериментальным данным. Нельзя считать известной функцию 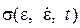 , если в заданным момент времени известны
, если в заданным момент времени известны  и
и  . Деформация до определенной величины может быть осуществлена различными путями, т.е. при одной и той же величине деформации, напряжения имеют существенно иные величины. Сами факты ползучести и релаксации показывают, что нет единой функции
. Деформация до определенной величины может быть осуществлена различными путями, т.е. при одной и той же величине деформации, напряжения имеют существенно иные величины. Сами факты ползучести и релаксации показывают, что нет единой функции  и попытки получить такого рода формулы обозначены на неудачу. В чем тут суть вопроса. На участке установившейся податливости при
и попытки получить такого рода формулы обозначены на неудачу. В чем тут суть вопроса. На участке установившейся податливости при  напряжение
напряжение 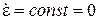 , а
, а  , т.е. релаксация не происходила бы. Если за время
, т.е. релаксация не происходила бы. Если за время  произошла деформация
произошла деформация  , то
, то  , так как не является функцией двух и более переменных, а зависит от всей функции
, так как не является функцией двух и более переменных, а зависит от всей функции  все стержни получат одинаковое удлинение
все стержни получат одинаковое удлинение  и деформации
и деформации  .
.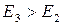 , а
, а  и модули упрочнения
и модули упрочнения  , т.е. поверхность изделия, в плоскости максимальной деформации, и его сердцевины имею не равные модули упругости (рис.3.10, а). Второй вариант - изделие с однородными свойствами до деформации, а в процессе нагружения стержни 1, 2, 3 получили различные пластические деформации (рис.3.10, в).
, т.е. поверхность изделия, в плоскости максимальной деформации, и его сердцевины имею не равные модули упругости (рис.3.10, а). Второй вариант - изделие с однородными свойствами до деформации, а в процессе нагружения стержни 1, 2, 3 получили различные пластические деформации (рис.3.10, в). , где
, где  - напряжение в стержне 2, а стержень 1 находится при той же нагрузке в пластическом состоянии и его деформацию можно представить в виде
- напряжение в стержне 2, а стержень 1 находится при той же нагрузке в пластическом состоянии и его деформацию можно представить в виде  , где
, где  и
и  - пластическая и упругая деформация соответственно. При снятии внешней нагрузки деформация и напряжение в стержне 1 убывает по линии АК, а в стержне 2 по линии
- пластическая и упругая деформация соответственно. При снятии внешней нагрузки деформация и напряжение в стержне 1 убывает по линии АК, а в стержне 2 по линии  .
. , а напряжение в последнем равно нулю, а в стержне 2
, а напряжение в последнем равно нулю, а в стержне 2  , т.е. стержень 2 еще упруго растянут и обладает потенциальной энергией
, т.е. стержень 2 еще упруго растянут и обладает потенциальной энергией  , т.е. под действием потенциальной энергии, соответствующей:
, т.е. под действием потенциальной энергии, соответствующей:  , стержень 2 будет продолжать укорачиваться. Так как стержни связаны поперечной 4, то укорачивающийся стержень 2 вызовет в стержне 1 деформацию и напряжение сжатия.
, стержень 2 будет продолжать укорачиваться. Так как стержни связаны поперечной 4, то укорачивающийся стержень 2 вызовет в стержне 1 деформацию и напряжение сжатия.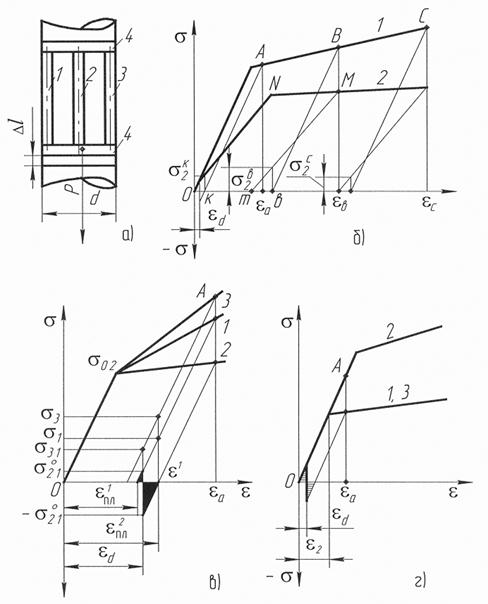
 . Во втором варианте разгрузки стержень 2 как и стержень 1 имеет пластическую, неравную деформацию и разгрузка идет по линиям Вв и Мм. При полной, разгрузке стержня 1,
. Во втором варианте разгрузки стержень 2 как и стержень 1 имеет пластическую, неравную деформацию и разгрузка идет по линиям Вв и Мм. При полной, разгрузке стержня 1, 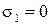 , а
, а  . Как и в первом случае укорачивающийся стержень 2 вызовет деформацию сжатия, которое будет происходить до полного упругого равновесия потенциальных энергий
. Как и в первом случае укорачивающийся стержень 2 вызовет деформацию сжатия, которое будет происходить до полного упругого равновесия потенциальных энергий  (рис.3.10, в) и, начиная с этой точки, происходили неодинаковые пластические деформации. Для упрочняющегося материала углы наклона кривых упрочнения стержней 1 … 3 неодинаковы при нагружении. Если разгрузить тело начиная от
(рис.3.10, в) и, начиная с этой точки, происходили неодинаковые пластические деформации. Для упрочняющегося материала углы наклона кривых упрочнения стержней 1 … 3 неодинаковы при нагружении. Если разгрузить тело начиная от 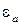 , то в точке
, то в точке  второй элемент будет свободен от напряжений, и первый будет нагружен напряжениями растяжения
второй элемент будет свободен от напряжений, и первый будет нагружен напряжениями растяжения  . Этим напряжениям соответствует некоторый уровень потенциальной энергии
. Этим напряжениям соответствует некоторый уровень потенциальной энергии  , вызывающий в стержне 2 напряжения сжатия. При равновесии стержень 2 упруго сжат
, вызывающий в стержне 2 напряжения сжатия. При равновесии стержень 2 упруго сжат  , а стержень 1 упруго растянут. Площади заштрихованных треугольников соответствуют уровняй потенциальных энергий
, а стержень 1 упруго растянут. Площади заштрихованных треугольников соответствуют уровняй потенциальных энергий  . Аналогичным образом можно описать поведение 3 стержня относительно 1 и 2. Таким образом, вследствие неодинаковых пластических деформации в поперечной сечении изделия механические свойства от элемента к элементу (от наружной поверхности зала к внутренней) различны, в результате чего появление остаточных напряжений неизбежно, а, следовательно, с учетом знака остаточные напряжения создают изгибающий момент, который и приводит к короблению готового изделия, а с учетом релаксационных процессов, это явление может проявляться через длительные периоды (месяцы после изготовления).
. Аналогичным образом можно описать поведение 3 стержня относительно 1 и 2. Таким образом, вследствие неодинаковых пластических деформации в поперечной сечении изделия механические свойства от элемента к элементу (от наружной поверхности зала к внутренней) различны, в результате чего появление остаточных напряжений неизбежно, а, следовательно, с учетом знака остаточные напряжения создают изгибающий момент, который и приводит к короблению готового изделия, а с учетом релаксационных процессов, это явление может проявляться через длительные периоды (месяцы после изготовления). начинается в точках
начинается в точках  . Интервал
. Интервал  соответствует вектору действительного упругого перемещения системы при разгрузке. В точке
соответствует вектору действительного упругого перемещения системы при разгрузке. В точке  , система упругих остаточных напряжения в элементах тела уравновешивается, и дальнейшее движение - разгрузка возможна только при обтачивании изделия (вала).
, система упругих остаточных напряжения в элементах тела уравновешивается, и дальнейшее движение - разгрузка возможна только при обтачивании изделия (вала). ;
;  ;
;  . (3.16)
. (3.16)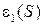 и
и  , продольная и поперечная деформация, а управляемые параметры
, продольная и поперечная деформация, а управляемые параметры  и
и  - внешнее напряжение, приложенное вдоль оси заготовки, и температура нагрева и охлаждения в зонах и узлах пучностей при механическом деформировании. Первый автономный канал управления продольной деформацией представляет собой контур обратной связи по отклонению, входом которого является продольная-осевая деформация
- внешнее напряжение, приложенное вдоль оси заготовки, и температура нагрева и охлаждения в зонах и узлах пучностей при механическом деформировании. Первый автономный канал управления продольной деформацией представляет собой контур обратной связи по отклонению, входом которого является продольная-осевая деформация  , а выходом напряжение, приложенное к одному из концов заготовки. В обратную связь контура управления включены последовательно три звена направленного действия, первичный преобразователь (датчик линейных перемещений) с передаточной функцией
, а выходом напряжение, приложенное к одному из концов заготовки. В обратную связь контура управления включены последовательно три звена направленного действия, первичный преобразователь (датчик линейных перемещений) с передаточной функцией  , дифференциальный усилитель
, дифференциальный усилитель  , на второй вход дифференциального усилителя подключен один из выходов контроллера
, на второй вход дифференциального усилителя подключен один из выходов контроллера  , последний согласно программе включает в работу контур управления осевой деформацией.
, последний согласно программе включает в работу контур управления осевой деформацией. , блок управления нагревом и охлаждением секций печи
, блок управления нагревом и охлаждением секций печи  , источник питания нагревательных элементов
, источник питания нагревательных элементов  , нагревательный элемент (ТЭН)
, нагревательный элемент (ТЭН) 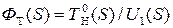
 .
. , последний включает в себя электропневмоклапан пропорционального действия; который управляет расходом воздуха поступающего с компрессора. Управление всеми каналами, согласно разработанным алгоритмам, осуществляется контроллером
, последний включает в себя электропневмоклапан пропорционального действия; который управляет расходом воздуха поступающего с компрессора. Управление всеми каналами, согласно разработанным алгоритмам, осуществляется контроллером  , а контур управления одним звеном, это не изменит физической сути, но даст четкое представление о взаимодействии объекта и САУ. На рис.3.11.1, а объект имеет на выходе деформацию (или напряжение нагружения), а на выходе напряжение (или деформацию). Статическая характеристика объекта с обратной связью показана на рис. 3.11.1, б.
, а контур управления одним звеном, это не изменит физической сути, но даст четкое представление о взаимодействии объекта и САУ. На рис.3.11.1, а объект имеет на выходе деформацию (или напряжение нагружения), а на выходе напряжение (или деформацию). Статическая характеристика объекта с обратной связью показана на рис. 3.11.1, б.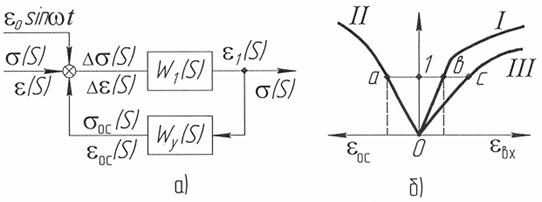
 и
и  удобно откладывать по горизонтальной оси вправо, а
удобно откладывать по горизонтальной оси вправо, а  - влево и строить характеристику контура управления во втором квадрате. При этом
- влево и строить характеристику контура управления во втором квадрате. При этом  , т.е. расстоянию " ав " (рис.3.11.1, б). Передвинуть отрезок " ав " вправо по горизонтали так, чтобы ее конец " а " совпал с точкой 1, найдем точку с искомой характеристики. При отрицательной обратной связи резулътатирующая характеристика объекта (кривая III) идет более полого, чем характеристика объекта без обратной связи, т.е. при одном и том же входном воздействии
, т.е. расстоянию " ав " (рис.3.11.1, б). Передвинуть отрезок " ав " вправо по горизонтали так, чтобы ее конец " а " совпал с точкой 1, найдем точку с искомой характеристики. При отрицательной обратной связи резулътатирующая характеристика объекта (кривая III) идет более полого, чем характеристика объекта без обратной связи, т.е. при одном и том же входном воздействии 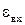 , с учетом обратной связи напряжение на выходе меньше. Если коэффициент усилия объекта
, с учетом обратной связи напряжение на выходе меньше. Если коэффициент усилия объекта  , табл.3.1, п.3. для стандартного тела, а контур обратной связи еет коэффициент усиления
, табл.3.1, п.3. для стандартного тела, а контур обратной связи еет коэффициент усиления  , то из выражения
, то из выражения  , где
, где  . При условии, что
. При условии, что  , коэффициент САУ к обращается в бесконечность, практически это значит, что линейное звено (объект управления) становится астатическим (нелинейное звено переходит в релейный режим). При работе САУ в астатическом режиме отклонение регулируемой величины стремится к нулю в независимости от величины внешнего воздействия при установившемся состоянии. Расчет астатизма системы представляет собой инженерную задачу и здесь не рассматривается. Применительно к процессу ТСО в качестве внешнего параметра может быть напряжение или деформация, если в качестве независимой переменной выступает напряжение, то неупругая релаксация проявляется как независимое от времени установления равновесного значения сопряженной переменной - деформации (или наоборот). Следует заметить, что внешнее проявление релаксации отражает просто поднастройку внутренних параметров материала к новым равновесным значениям и для каждого значения приложенного напряжения. Существует равновесное значение внутреннего параметра и по мере релаксации внутреннего параметра к равновесному значению, деформация также стремится к соответствующему равновесному значению. Изменение внутренних параметров может происходить в результате кинематических процессов, таких как диффузия. Внешним проявлением внутренней релаксации являются зависимые от времени деформационные свойства.
, коэффициент САУ к обращается в бесконечность, практически это значит, что линейное звено (объект управления) становится астатическим (нелинейное звено переходит в релейный режим). При работе САУ в астатическом режиме отклонение регулируемой величины стремится к нулю в независимости от величины внешнего воздействия при установившемся состоянии. Расчет астатизма системы представляет собой инженерную задачу и здесь не рассматривается. Применительно к процессу ТСО в качестве внешнего параметра может быть напряжение или деформация, если в качестве независимой переменной выступает напряжение, то неупругая релаксация проявляется как независимое от времени установления равновесного значения сопряженной переменной - деформации (или наоборот). Следует заметить, что внешнее проявление релаксации отражает просто поднастройку внутренних параметров материала к новым равновесным значениям и для каждого значения приложенного напряжения. Существует равновесное значение внутреннего параметра и по мере релаксации внутреннего параметра к равновесному значению, деформация также стремится к соответствующему равновесному значению. Изменение внутренних параметров может происходить в результате кинематических процессов, таких как диффузия. Внешним проявлением внутренней релаксации являются зависимые от времени деформационные свойства. или проходит через него, а некоторые стали (40Н), имеют участки повышенного значения предела текучести при нагреве.
или проходит через него, а некоторые стали (40Н), имеют участки повышенного значения предела текучести при нагреве.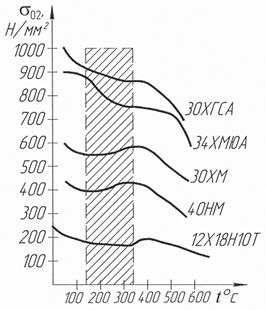
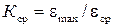 .
. , близкое к единице, свидетельствует об однородности пластических деформаций материала по всей длине заготовки. На рис. 3.6 представлены значения коэффициента
, близкое к единице, свидетельствует об однородности пластических деформаций материала по всей длине заготовки. На рис. 3.6 представлены значения коэффициента 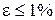 наблюдается значительный разброс данных и большое значение коэффициента
наблюдается значительный разброс данных и большое значение коэффициента 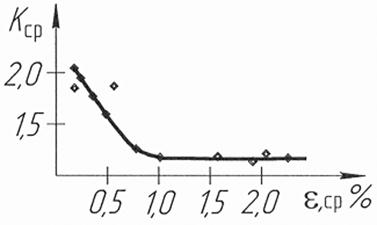
 , контроль же за локализацией деформаций на определенном участке вала (например, в зонах и узлах пучности высших гармоник) при нагреве возможен только в поперечном сечении, т.к. измерение относительной осевой продольной деформации при ТСО невозможно из-за отсутствия технических средств измерений. Согласно разработанной технологии ТСО изделие растягивают (например, при температуре со слабо выраженной зависимостью упругости от температуры) до желаемой степени деформации, затем, если равномерность пластической деформации неудовлетворительна, участки с высокой степенью деформации неудовлетворительна, участки с высокой степенью деформации быстро охлаждают, а слабо деформированные нагревают и с получением заданной деформации температуру снова повышают до прежнего значения и так повторяют до тех пор, пока не обеспечат равномерное деформирование всего объема металла по всей длине изделия, при этом скорость деформации во время охлаждения и нагрева снижают в 2 - 3 раза. Таким образом, рассмотренный этап ТСО позволяет устранить технологическую наследственность от предыдущих операций, стабилизировать уровень остаточных напряжений в сечении и по длине изделия, создавая при этом остаточные напряжения одного знака, одновременно провести правку длинномерных заготовок, если в процессе предыдущих операций изделие покоробилось.
, контроль же за локализацией деформаций на определенном участке вала (например, в зонах и узлах пучности высших гармоник) при нагреве возможен только в поперечном сечении, т.к. измерение относительной осевой продольной деформации при ТСО невозможно из-за отсутствия технических средств измерений. Согласно разработанной технологии ТСО изделие растягивают (например, при температуре со слабо выраженной зависимостью упругости от температуры) до желаемой степени деформации, затем, если равномерность пластической деформации неудовлетворительна, участки с высокой степенью деформации неудовлетворительна, участки с высокой степенью деформации быстро охлаждают, а слабо деформированные нагревают и с получением заданной деформации температуру снова повышают до прежнего значения и так повторяют до тех пор, пока не обеспечат равномерное деформирование всего объема металла по всей длине изделия, при этом скорость деформации во время охлаждения и нагрева снижают в 2 - 3 раза. Таким образом, рассмотренный этап ТСО позволяет устранить технологическую наследственность от предыдущих операций, стабилизировать уровень остаточных напряжений в сечении и по длине изделия, создавая при этом остаточные напряжения одного знака, одновременно провести правку длинномерных заготовок, если в процессе предыдущих операций изделие покоробилось. , (3.17)
, (3.17)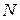 - число дислокаций в стенке;
- число дислокаций в стенке;  - среднее расстояние между дислокациями;
- среднее расстояние между дислокациями;  - модуль сдвига;
- модуль сдвига; 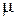 - коэффициент Пуансона. Из микроструктур следует, что
- коэффициент Пуансона. Из микроструктур следует, что  ,
,  м,
м, 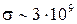 Н/м2.
Н/м2. и, главное, осевых
и, главное, осевых  напряжений в поверхностном слое.
напряжений в поверхностном слое. , (3.18)
, (3.18)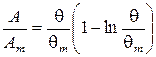 , (3.19)
, (3.19) - энергия границ зерен;
- энергия границ зерен;  - максимальная энергия границ зерен;
- максимальная энергия границ зерен; 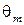 - угол разориентации, при котором энергия границы максимальна. Плотность дислокаций и напряжения вблизи границы пропорциональны углу разориентировки
- угол разориентации, при котором энергия границы максимальна. Плотность дислокаций и напряжения вблизи границы пропорциональны углу разориентировки  . Следовательно, диффузия дислокаций приводит к выравниванию угла
. Следовательно, диффузия дислокаций приводит к выравниванию угла 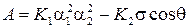 , (3.20)
, (3.20) - направляющие косинусы для двух других осей.
- направляющие косинусы для двух других осей. (3.21)
(3.21)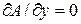 получили зависимость
получили зависимость  .
. (3.22)
(3.22) и дисперсией
и дисперсией  .
. . Тогда структурная перестройка происходит в той части зерен, для которой сжимающее напряжение
. Тогда структурная перестройка происходит в той части зерен, для которой сжимающее напряжение  .
.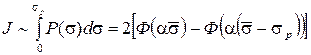 , (3.23)
, (3.23) - интеграл вероятности, функция Лапласа.
- интеграл вероятности, функция Лапласа. .
. . (3.24)
. (3.24) - напряжение сдвига;
- напряжение сдвига;  - вектор Бюргерса, величина которого равна порядку постоянной решетки; u - расстояние между дислокациями.
- вектор Бюргерса, величина которого равна порядку постоянной решетки; u - расстояние между дислокациями.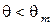 . Энергия границы при этом уменьшается и состояние становится более равновесным.
. Энергия границы при этом уменьшается и состояние становится более равновесным.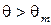 , то уменьшение угла раз ориентировки связано с увеличением энергии границ. Очевидно, это возможно только в том случае, если длина границы уменьшится. Для таких зерен будет происходить смещение границ: более мелкие зерна растут за счет более крупных. В этом случае также достигается большая однородность. Скорость деформации определяется вязкостью
, то уменьшение угла раз ориентировки связано с увеличением энергии границ. Очевидно, это возможно только в том случае, если длина границы уменьшится. Для таких зерен будет происходить смещение границ: более мелкие зерна растут за счет более крупных. В этом случае также достигается большая однородность. Скорость деформации определяется вязкостью . (3.25)
. (3.25) - превышение напряжения предела сдвиговой текучести.
- превышение напряжения предела сдвиговой текучести.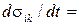
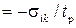 , т.е. происходит по экспоненциальному закону, где:
, т.е. происходит по экспоненциальному закону, где:  - время релаксации, которое можно оценить из соотношения
- время релаксации, которое можно оценить из соотношения  .
.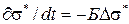 , (3.26)
, (3.26) - напряжение первого рода;
- напряжение первого рода; 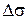 - оператор Лапласа;
- оператор Лапласа;  - кинетический параметр, аналогичный коэффициенту диффузии. Можно получить соотношение
- кинетический параметр, аналогичный коэффициенту диффузии. Можно получить соотношение , (3.27)
, (3.27) , получим зависимость от времени.
, получим зависимость от времени. . (3.28)
. (3.28) - расстояние от границы раздела;
- расстояние от границы раздела;  - интеграл вероятности Гаусса, эта функция табулированная, ее значения приведены в соответствующих математических таблицах.
- интеграл вероятности Гаусса, эта функция табулированная, ее значения приведены в соответствующих математических таблицах. ;
; 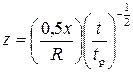 . (3.29)
. (3.29) получено с учетом соотношения (3.19), из (3.20, 3.21) видно, что релаксация напряжений первого рода определяется размерами зерен и временем релаксации, напряжения второго рода. Роль осевых наполнений состоит не только в том, чтобы создать условия для скольжения дислокаций, но такие в том, чтобы установилось равновесное распределение, симметрическое относительно оси изделия (зала). Очевидно, что после релаксации напряжений в силу осевой симметрии осевые, радиальные и касательные напряжения не зависят от
получено с учетом соотношения (3.19), из (3.20, 3.21) видно, что релаксация напряжений первого рода определяется размерами зерен и временем релаксации, напряжения второго рода. Роль осевых наполнений состоит не только в том, чтобы создать условия для скольжения дислокаций, но такие в том, чтобы установилось равновесное распределение, симметрическое относительно оси изделия (зала). Очевидно, что после релаксации напряжений в силу осевой симметрии осевые, радиальные и касательные напряжения не зависят от  и
и  , здесь
, здесь  и
и  , (3.30)
, (3.30)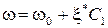 ,
,  ,
,  - собственная частота системы без учета неупругого сопротивления;
- собственная частота системы без учета неупругого сопротивления;  и
и  - нелинейная поправки;
- нелинейная поправки;  - малый параметр. Величины
- малый параметр. Величины  - масса.
- масса. .
. ,
, 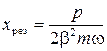 . (3.31)
. (3.31) ,
,  . (3.32)
. (3.32) - объем рассматриваемого элемента.
- объем рассматриваемого элемента. (
( - остаточные напряжения петли) дислокаций - источники Франка - Рида. Тепловые колебания не могут привести к генерации петель дислокаций, так как энергия тепловых колебаний много меньше энергии, необходимой для образования петли. Роль тепловых колебаний, т.е. роль фактора хаотического движения, в данном случае играют высокочастотные колебания второй, третьей и более мод.
- остаточные напряжения петли) дислокаций - источники Франка - Рида. Тепловые колебания не могут привести к генерации петель дислокаций, так как энергия тепловых колебаний много меньше энергии, необходимой для образования петли. Роль тепловых колебаний, т.е. роль фактора хаотического движения, в данном случае играют высокочастотные колебания второй, третьей и более мод. , (3.33)
, (3.33)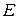 - модуль Юнга;
- модуль Юнга;  - вектор Бюргерса;
- вектор Бюргерса;  - длина участка заторможенной дислокации.
- длина участка заторможенной дислокации. , (3.34)
, (3.34) - плотность материала.
- плотность материала. . (3.35)
. (3.35) ,
,  , следовательно, из (3.33 … 3.35) получим
, следовательно, из (3.33 … 3.35) получим .
. , то
, то  независимо от вибрационного воздействия,
независимо от вибрационного воздействия,  определяется скоростью деформации
определяется скоростью деформации 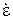
 , (3.36)
, (3.36) . от параметров внешнего воздействия и от исходного состояния материала
. от параметров внешнего воздействия и от исходного состояния материала , (3.37)
, (3.37) ,
,  ,
,  .
. . Резонансное поглощение зависит от амплитуды вынужденных колебаний и постоянного напряжения. Наблюдается резкое возрастание логарифмического декремента при напряжении
. Резонансное поглощение зависит от амплитуды вынужденных колебаний и постоянного напряжения. Наблюдается резкое возрастание логарифмического декремента при напряжении  .
. , поэтому, чтобы сохранить прочностные характеристики материала изделия (зала) после виброобработки и охлаждения, нагрев до температуры выше 350°С нежелателен. Эффективная область динамического воздействия на рис.3.12 заштрихована. Кроме того, вибрационная обработка при высокой температуре может привести к локальным деформациям изделия под действием приложенных динамических напряжений, что при охлаждении приводит к появлению локальных напряженных областей. Кроме того, известно, что вибрационный процесс в несколько раз сокращает время релаксации напряжений, а, следовательно, повышает производительность ТСО.
, поэтому, чтобы сохранить прочностные характеристики материала изделия (зала) после виброобработки и охлаждения, нагрев до температуры выше 350°С нежелателен. Эффективная область динамического воздействия на рис.3.12 заштрихована. Кроме того, вибрационная обработка при высокой температуре может привести к локальным деформациям изделия под действием приложенных динамических напряжений, что при охлаждении приводит к появлению локальных напряженных областей. Кроме того, известно, что вибрационный процесс в несколько раз сокращает время релаксации напряжений, а, следовательно, повышает производительность ТСО.