 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Упругая система станкаАнализ упругой системы, как элемента динамической системы станка, включает определение: 1) собственной устойчивости этого элемента; 2) статических и динамических характеристик по резанию, трению и процессам в двигателе: Упругая система станка имеет особенности, характерные также и для других машин, отличающие ее от упругих систем строительных конструкций. Особенности упругой системы сводятся к следующему. 1. Наличие большого числа подвижных соединений, т.е. таких соединений, в которых детали станка имеют заданное относительное движение. 2. Наличие большого числа неподвижных слабо затянутых соединений. Следует различать собственную устойчивость упругого элемента и эквивалентной упругой системы. Потеря устойчивости упругими элементами в станках встречается сравнительно редко и носит в основном статический характер. Потеря устойчивости может возникать в следующих случаях: 1. При работе длинных ходовых винтов, штоков, сверл для глубокого сверления и т.п. деталей на сжатие (продольный изгиб). 2. При вращении валов, длинных заготовок, сверл и т.п. с числом оборотов, близким к критическому. 3. При обработке тонкостенных заготовок или при использовании в станке тонкостенных деталей. Характеристики упругой системы определяются следующими основными параметрами: массами или моментами инерции узлов и деталей; жесткостью упругих элементов; силами неупругого сопротивления (демпфирования); связями между перемещениями масс в системе с многими степенями свободы. Смысл и значение этих параметров общеизвестны: они подробно рассматриваются в курсах теоретической механики и теории колебаний. Мы остановимся на них в той мере, в которой это необходимо для понимания дальнейшего материала. Силы неупругого сопротивления или силы демпфирования в упругих элементах станка определяются в основном трением в стыках деталей. Поскольку в неподвижных стыках, в отличие от подвижных, относительное смещение деталей возникает только в результате деформации упругой системы, постольку силы трения в них всегда демпфируют колебания, рассеивают часть энергии, вносимой в УС при ее нагружении. Важнейшей особенностью упругой системы, вытекающей из того, что она имеет много степенной свободы, является зависимость между собой отдельных перемещений УС, или, иначе, наличие связей ее обобщенных координат. Эти связи ниже будем называть внутренними связями УС. Проявляются эти связи в том, что при попытке вызвать данной силой какое-либо перемещение, вызывают также и другие перемещения. Различают связи статические (по координате), скоростные (по первой производной координаты по времени) и динамические, инерционные (по второй производной координаты по времени). Статическая или упругая (координатная) связь может возникнуть как между поступательными перемещениями, так и между угловым (крутильным) и поступательным. Эта связь возникает тогда, когда перемещения рассматриваемой массы (точки) являются суммой деформаций нескольких пружин, несущих другие массы. Одним из важных случаев возникновения связи является несовпадение действующей силы с направлением главных осей жесткости УС. Простейшим и наглядным примером для этого случая является «косой изгиб» балки прямоугольного сечения. Скоростная связь возникает в тех случаях, когда в системе действуют силы, являющиеся функциями скорости. Демпфирующие силы вносят связь тогда, когда демпфирование по одной обобщенной координате оказывает влияние на демпфирование по другой координате. Это бывает, например, при несовпадении осей координат и направления деформаций в плоскости стыка. Инерционная или динамическая связь возникает в упругой системе при наличии многих масс и в тех случаях, когда равнодействующая сил инерции не совпадает с центром жесткости системы. Статическими и динамическими характеристиками УС называются зависимости, выражающие отношение выходной координаты, т.е. смещение системы или скорости этого смещения, к входной координате, т.е. силе (или к иному, например, тепловому воздействию). Входные и выходные координаты УС определяются в каждом конкретном случае путем анализа динамической системы станка. По контурам связи с резанием и трением выходной координатой чаще всего является линейное смещение по нормали к поверхности резания или к поверхности трения. Среди характеристик УС по связям с различными рабочими процессами особое место занимает характеристика по связи с резанием, поскольку она непосредственно определяет влияние УС на качество обрабатываемой детали. Характеристика
Статическая характеристика выражается коэффициентом КУС, характеризующим податливость системы. Динамическая характеристика УС, выраженная в частотной форме, носит в теории колебаний название динамической податливости, а обратная ей величина – динамической жесткости. Эта характеристика отражает важную особенность УС, заключающуюся в том, что деформация системы зависит не только от величины действующей сил. Но и от частоты ее изменения. При совпадении частоты изменения силы с одной из собственных частот системы деформации или смещения системы резко возрастают – наступает явление резонанса. Для анализа динамических характеристик сложных упругих систем удобно во многих случаях пользоваться упомянутым выше представлением о нормальных координатах. Независимые УС, каждая из которых описывается нормальной координатой, можно представить как отдельные элементы системы, уравнения которых имеют второй порядок:
где Интересующее нас перемещение – выходная координата
На рис.1.5 показана схема УС с одной степенью свободы, параметры которой соответствуют «приведенным» параметрам системы, описываемой одной из нормальных координат. В типовой форме ее передаточная функция, как характеристика колебательного звена, имеет вид, получаемый преобразованием одного из уравнений (1.17), в котором для удобства опускаем индексы:
где Из выражения (1.19) получаем амплитудно-фазовую частотную характеристику УС, описываемой одной нормальной координатой
Здесь значения На рис.1.5, а показана амплитудно-фазовая частотная характеристика УС с одной степенью свободы. Она построена в комплексной плоскости по выражению (1.20) в прямоугольных координатах Располагая характеристиками для каждой нормальной координаты, можно определить динамическую характеристику сложной упругой системы. Сложная упругая система, определяемая нормальными координатами, является системой параллельно соединенных элементов, у которых входная координата одна – сила Q, а выходные координаты – перемещения Характеристика такой системы равна сумме характеристик элементов, т.е. характеристик колебательных систем с одной степенью свободы, определяемых каждая своей нормальной координатой.
Рис.1.6. Схема УС с одной степенью свободы и ее частотные характеристики: а – амплитудно-фазовая; б – вещественная, мнимая, амплитудная, фазовая.
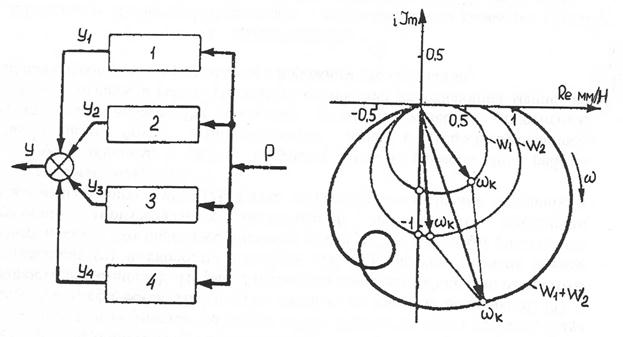
Рис.1.6. Схема УС в нормальных координатах (а) и пример суммирования характеристик с одинаковыми знаками: амплитудно-фазовых (б)
На рис.1.6 показана схема сложной УС в нормальных координатах. Для определенности взята УС по связи с резанием. Для нее Q=P;
На том же рисунке показано суммирование двух характеристик, имеющих одинаковый знак.
Дата добавления: 2015-01-18 | Просмотры: 1279 | Нарушение авторских прав |
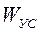 упругой системы по связи с резанием выражает отношение смещения У инструмента и заготовки по нормали к поверхности резания к внешней силе Р, действующей так же, как сила резания, - имитирующей силу резания
упругой системы по связи с резанием выражает отношение смещения У инструмента и заготовки по нормали к поверхности резания к внешней силе Р, действующей так же, как сила резания, - имитирующей силу резания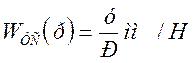 (1.16)
(1.16)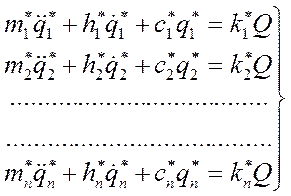 . (1.17)
. (1.17)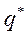 - нормальная координата;
- нормальная координата;  ,
,  ,
,  - приведенная масса, коэффициент демпфирования и жесткость данной нормальной УС; Q – внешняя обобщенная сила, действующая на УС и имитирующая входное воздействие;
- приведенная масса, коэффициент демпфирования и жесткость данной нормальной УС; Q – внешняя обобщенная сила, действующая на УС и имитирующая входное воздействие; 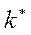 - коэффициент «приведения» внешней силы к нормальной координате.
- коэффициент «приведения» внешней силы к нормальной координате. системы – получается алгебраическим суммированием перемещений по отдельным нормальным координатам:
системы – получается алгебраическим суммированием перемещений по отдельным нормальным координатам: . (1.18)
. (1.18)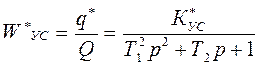 , (1.19)
, (1.19) - приведенная статическая характеристика (податливость) данной нормальной системы в мм/Н;
- приведенная статическая характеристика (податливость) данной нормальной системы в мм/Н; 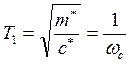 - инерционная постоянная времени в сек;
- инерционная постоянная времени в сек;  - постоянная времени демпфирования в сек;
- постоянная времени демпфирования в сек;  - логарифмический декремент;
- логарифмический декремент; 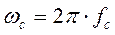 - собственная круговая частота колебаний в 1/сек;
- собственная круговая частота колебаний в 1/сек;  - число собственных колебаний в секунду или, иначе, собственная частота колебаний в гц.
- число собственных колебаний в секунду или, иначе, собственная частота колебаний в гц.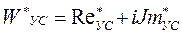 , (1.20)
, (1.20) ; (1.21)
; (1.21)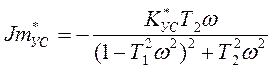 . (1.22)
. (1.22) и
и  имеют размерность податливости мм/н.
имеют размерность податливости мм/н. и
и  .
. алгебраически суммируются.
алгебраически суммируются.
 и соответственно выражению (1.18)
и соответственно выражению (1.18)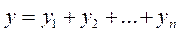 .
.