 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
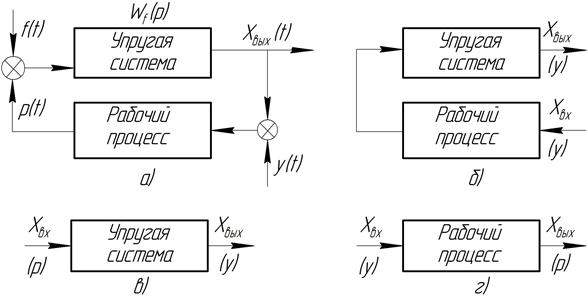
Статические и динамические характеристики элементов и системНаправленность связей позволяет для удобства анализа расчленять динамическую систему, «размыкая» связи между элементами. Если размыкание произведено по одной из связей (рис.1.3), то система (одноконтурная) называется разомкнутой. Понятие разомкнутой системы, являясь условным, необходимо при оценке динамических свойств замкнутой системы частотными методами. Разорвав две связи, можно выделить элемент системы и рассматривать его отдельно, изучая его свойства в виде зависимости между входной и выходной координатами элемента. Соответственно можно говорить о зависимости между входной и выходной координатами системы. Эту зависимость будем называть характеристикой элемента или системы. Если она получена в условиях, когда входная координата не изменяется во времени, то характеристика будет статической.
Рис.1.3. Схема размыкания одноконтурной динамической системы: а – замкнутая система; б – разомкнутая система; в и г – элементы системы
Та же зависимость, полученная при изменяющейся во времени входной координате, является динамической характеристикой. Размерность характеристики определяется отношением размерности выходной координаты к входной. Встречающиеся на практике характеристики элементов и систем, как правило, нелинейны. Например, статическая характеристика УС, т.е. зависимость деформации УС станка от действующей силы, выражается известной петлеобразной кривой. Параметры систем в большей или меньшей степени являются переменными во времени или по координатам. Эти параметры также являются всегда распределенными. Для упрощения анализа стремятся перейти к системам с постоянными сосредоточенными параметрами, а характеристики линеаризуют, т.е. представляют в виде обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами. Такая характеристика элемента или системы в виде отношения выходной координаты к входной или внешнему воздействию, записанная в операторной форме, называется передаточной функцией W (p) элемента или системы. Для элемента передаточная функция имеет вид
где Передаточная функция разомкнутой системы Wраз (p) имеет тот же вид, но является безразмерной, так как ее входная и выходная координаты имеют одинаковую размерность. В анализируемых станочных динамических системах, как правило, степень многочлена Из уравнения (1.2) при
при
Передаточные функции одноконтурной замкнутой системы выражаются через передаточную функцию разомкнутой системы следующим образом:
где
При последовательном соединении элементов передаточная функция системы равна произведению передаточных функций элементов. При параллельном – их сумме. При анализе динамических систем очень удобны так называемые частотные методы. В этом случае применяются частотные динамические характеристики, определяемые во времени по закону гармонических колебаний. Частота ω этих колебаний варьируется теоретически от нуля до бесконечности, а практически – в пределах интересующего нас диапазона частот, который называют рабочим. Зависимость отношения амплитуд колебания выходной и входной координат от частоты дает амплитудно-частотную характеристику; зависимость фазы колебаний – фазово-частотную; совмещение этих двух характеристик – амплитудно-фазовую частотную характеристику. Амплитудно-фазовая частотная характеристика строится в комплексной плоскости, как показано на рис.1.4.
Рис.1.4. Частотные характеристики: а – запись изменения входной и выходной координаты при заданной частоте
Переход от передаточной функции Тогда, соответственно выражениями (1.4), (1.5), (1.6), (1.7) и (1.8) амплитудно-фазовые частотные характеристики имеют вид: для звена
Для замкнутой системы по внешнему воздействию
Для замкнутой системы по изменению настройки
Амплитудно-фазовая частотная характеристика разомкнутой системы
где
Переход от одной формы к другой осуществляется в соответствии со следующим выражением:
Зависимости Re и Jm от частоты ω дают вещественную и мнимую частотные характеристики, а зависимости А и Характеристики параллельно и последовательно соединенных звеньев складываются и умножаются по правилам сложения и умножения комплексных чисел при сложении раздельно складываются вещественные и мнимые части или векторно складываются амплитуды при заданных частоте и фазах. При умножении перемножаются амплитуды (модули) и складываются фазы (аргументы). Частотные методы анализа и частотные характеристики применимы только к линейным системам. Однако в ряде случаев их используют и в существенно нелинейных задачах в виде эквивалентных характеристик (метод гармонической линеаризации). Широко используются так называемые временные динамические характеристики, получаемые при заданном законе изменения входной координаты от одного установившегося значения к другому. Статические и динамические характеристики могут быть представлены в графической и аналитической форме. Характеристики можно получить теоретически и экспериментально. При экспериментальном построении с помощью специального устройства создается выбранное изменение входной координаты и фиксируется соответствующее ему изменение выходной координаты. Например, при определении частотной характеристики упругой системы вибратором того или иного типа создается периодическое силовое воздействие, соответствующее входной координате (например, силе резания). Датчиком фиксируется смещение точек УС, определяющее выходную координату (например, относительное смещение резца и обрабатываемой детали). Статические и динамические характеристики могут применяться для описания свойств отдельных элементов и систем в целом. Устойчивость систем и элементов Важнейшим условием, необходимым для определения характеристики, является устойчивость элемента или системы. Иначе говоря, это условие определяет работоспособность элемента или системы. Для того чтобы отличить устойчивость элемента от устойчивости анализируемой системы, часто говорят о собственной устойчивости элемента. Принципиальной разницы между этими понятиями нет, поскольку элемент всегда является сложной системой со своими внутренними связями. Для устойчивости нелинейной системы, имеющей непрерывные координаты и их производные в окрестности рассматриваемого состояния, по А.М.Ляпунову необходима и достаточна устойчивость первого линейного приближения. Устойчивость определяется нарастанием или уменьшением во времени переходной составляющей решения уравнения (1.1):
где
В общем случае корни являются комплексными:
Система устойчива, если вещественные части корней отрицательны. Соблюдение этого условия устойчивости определяется с помощью так называемых критериев устойчивости. Известны алгебраические (Рауса, Гурвица и др.) и частотные (Найквиста, или амплитудно-фазовый, Михайлова и др.) критерии устойчивости. Амплитудно-фазовый критерий, или критерий Найквиста, позволяет по характеристике разомкнутой системы судить об устойчивости замкнутой системы. Практически критерий удобен в тех случаях, когда разомкнутая система устойчива или нейтральна, а в передаточной функции этой системы степень многочлена, стоящего в знаменателе, выше или равна степени многочлена, стоящего в числителе. При этих условиях для устойчивости соответствующей замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы
Рис.1.5. Амплитудно-фазовые частотные характеристики (АФЧХ) разомкнутой системы
В этом простейшем виде критерий широко используется в данной работе, так как рассматриваемые динамические системы станков удовлетворяют указанным условиям. Отрезок, отсекаемый характеристикой разомкнутой системы на отрицательной ветви вещественной оси, обозначим
в котором оно применяется далее к различным системам. Дата добавления: 2015-01-18 | Просмотры: 1812 | Нарушение авторских прав |
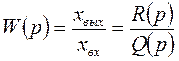 , (1.4)
, (1.4)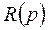 и
и 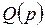 - операторные многочлены.
- операторные многочлены.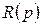 меньше степени многочлена
меньше степени многочлена 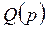 . Для замкнутой одноконтурной системы (см.рис.1.3) будем различать передаточные функции по внешнему воздействию Wf (p) и по настройке Wу (p).
. Для замкнутой одноконтурной системы (см.рис.1.3) будем различать передаточные функции по внешнему воздействию Wf (p) и по настройке Wу (p).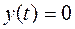
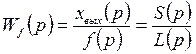 ; (1.5)
; (1.5)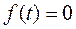
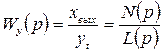 . (1.6)
. (1.6)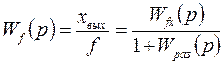 ; (1.7)
; (1.7)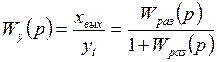 , (1.8)
, (1.8)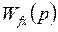 - добавочная передаточная функция УС отдельно взятого звена системы по
- добавочная передаточная функция УС отдельно взятого звена системы по 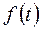 при
при 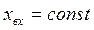 ;
;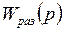 - передаточная функция разомкнутой системы при
- передаточная функция разомкнутой системы при 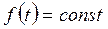 ;
; 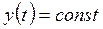 .
.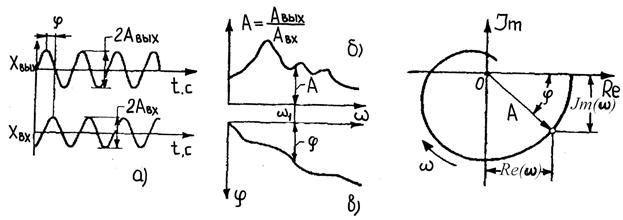
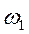 ; б – амплитудно-частотная характеристика; в – фазово-частотная характеристика; г – амплитудно-фазовая характеристика.
; б – амплитудно-частотная характеристика; в – фазово-частотная характеристика; г – амплитудно-фазовая характеристика. к частотной амплитудно-фазовой характеристике
к частотной амплитудно-фазовой характеристике 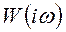 производится заменой символа дифференцирования р на
производится заменой символа дифференцирования р на 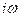 , где I – мнимая единица, а ω – круговая частота.
, где I – мнимая единица, а ω – круговая частота.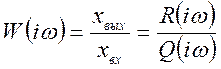 , (1.9)
, (1.9)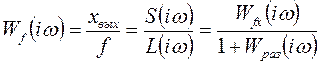 . (1.10)
. (1.10)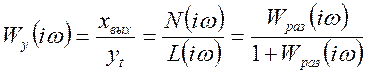 . (1.11)
. (1.11)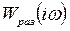 имеет вид выражения (1.9). Амплитудно-фазовая частотная характеристика
имеет вид выражения (1.9). Амплитудно-фазовая частотная характеристика 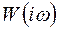 является комплексной величиной и после преобразования выражений (1.9), (1.10) и (1.11) может быть представлена в следующих двух формах:
является комплексной величиной и после преобразования выражений (1.9), (1.10) и (1.11) может быть представлена в следующих двух формах: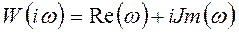 , (1.12)
, (1.12)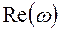 - вещественная часть;
- вещественная часть; 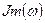 - мнимая часть,
- мнимая часть,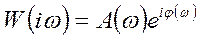 , (1.13)
, (1.13)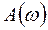 - амплитуда, равная отношению амплитуды выходной координаты к амплитуде входной;
- амплитуда, равная отношению амплитуды выходной координаты к амплитуде входной;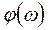 - фаза между колебаниями входной и выходной координаты.
- фаза между колебаниями входной и выходной координаты.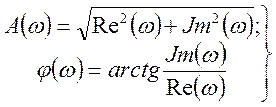 . (1.14)
. (1.14)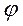 - амплитудную и фазовую. Имеются и другие разновидности частотных характеристик (логарифмические).
- амплитудную и фазовую. Имеются и другие разновидности частотных характеристик (логарифмические).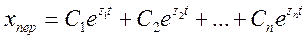 , (1.15)
, (1.15)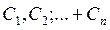 - произвольные постоянные, определяемые заданными начальными условиями процесса;
- произвольные постоянные, определяемые заданными начальными условиями процесса;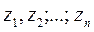 - корни характеристического уравнения
- корни характеристического уравнения 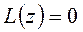 .
.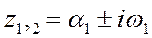 .
.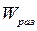 (характеристика является безразмерной) не охватывала точку с координатой – 1, лежащую на вещественной оси. На рис.1.5 показаны характеристики разомкнутой системы для устойчивой а и неустойчивой б замкнутых систем.
(характеристика является безразмерной) не охватывала точку с координатой – 1, лежащую на вещественной оси. На рис.1.5 показаны характеристики разомкнутой системы для устойчивой а и неустойчивой б замкнутых систем.
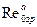 . Тогда условие устойчивости получит вид
. Тогда условие устойчивости получит вид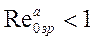 ,
,