|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
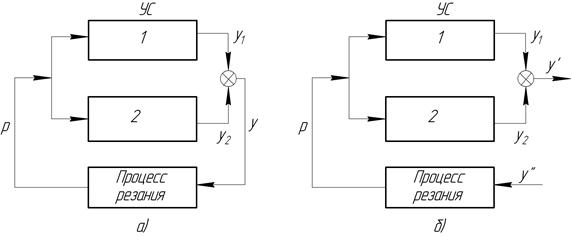
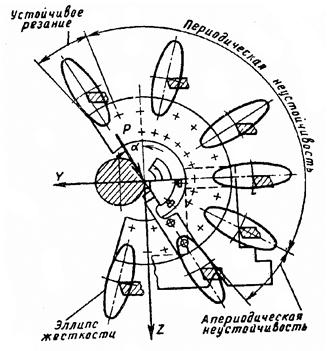
Упругой системы и резанииИз методических соображений вначале рассмотрим случай, когда процесс резания описывается статической характеристикой. Это соответствует условиям существенной малости постоянных времени процесса резания по сравнению с постоянными времени УС. В сочетании с УС, представляемой в виде колебательной системы с одной степенью свободы, процесс резания, описываемый статической характеристикой по толщине срезаемого слоя, дает устойчивую систему. Характеристика разомкнутой системы при этом не пересекает отрицательной ветви вещественной оси. В общем случае характеристика УС может быть представлена суммой характеристик отдельных нормальных форм колебаний. Влияние этой особенности УС нагляднее всего может быть выяснено на примере УС с двумя ориентированными в пространстве осями жесткости, т.е. системы с двумя степенями свободы с координатной связью. Контур связи этой системы и процесса резания показаны на рис.4.1, где 1 и 2 обозначены обе нормальные формы УС. Знак перед одной из характеристик нормальных форм отражает принципиальную особенность системы с многими степенями свободы. Она положена в основу объяснения условий появления автоколебаний при резании в так называемой «теории координатной связи».
Рис.1.13. Схема эквивалентной динамической системы станка (с резанием): а – замкнутой; б – разомкнутой
Применим амплитудно-фазовый критерий для оценки устойчивости системы. Для этого разомкнем систему, как показано на рис. 4.1, и построим амплитудно-фазовую характеристику разомкнутой системы. Характеристика, типовые формы которой показаны на рис.1.14, получается умножением характеристик УС и процесса резания. В данном случае это делается простым изменением масштаба амплитудно-фазовой характеристики УС пропорционально коэффициенту резания. Шкала получается безразмерной. Суммирование характеристик нормальных форм УС с разными знаками дает характеристику типа II, пересекающую отрицательную ветвь вещественной оси, т.е. потенциально неустойчивую. Суммирование характеристик нормальных форм разного знака, чему соответствует характеристика I типа, этого эффекта не дает. В последнем случае система может стать устойчивой только вследствие отставания силы резания от изменения сечения срезаемого слоя, выражаемого динамической характеристикой резания. Если характеристика пересекает отрицательную вещественную ось между 0 и -1, то система, являясь потенциально неустойчивой, при данных значениях параметров устойчива. Так как коэффициент резания пропорционален ширине срезаемого слоя, то, пользуясь описанным построением, можно оценить предельную ширину Отсюда
Чем больше отрезок Эта закономерность хорошо согласуется другой: чем больше отрезок, отсекаемый характеристикой УС на положительной вещественной оси, тем ниже технологическая жесткость системы и тем меньше точность обработки или, иначе, - тем сильнее влияние деформаций системы на точность обработки. Физический смысл явления потери устойчивости системой при описании процесса резания статической характеристикой иллюстрируется схемой (рис.4.3) и заключается следующем. Наличие многих степеней свободы УС приводит к тому, что колебания инструмента относительно заготовки, представляют результат сложения нескольких связанных между собой простейших (поступательных или крутильных) колебаний. В приведенном примере системы с двумя степенями свободы складываются два поступательных колебаний по осям ξ и v. Между этими колебаниями существует тот или иной сдвиг во времени – фазовый сдвиг. Поэтому образующаяся в результате сложения колебаний траектория относительного движения инструмента и заготовки имеет форму замкнутой кривой, теоретически – форму эллипса. Этот эллипс в отличие от эллипса жесткости будем называть эллипсом перемещений.
Рис.1.14. Определение устойчивости эквивалентной динамической системы с резанием (III типа). Амплитудно-фазовые частотные характеристики: а – эквивалентной упругой системы
Двигаясь по такой траектории показанной на рис.1.15 последовательными положениями вершины резца, инструмент изменяет толщину срезаемого слоя, а следовательно, силу резания таким образом, что при движении в сторону действия силы резания толщина срезаемого слоя больше, чем при движении инструмента навстречу силе резания. На рис.1.15 показано отдельно каждое последовательное положение вершины резца и изменение толщины срезаемого слоя в процессе возникших колебаний. Площадь диаграммы, очерченной кривой изменения силы резания по перемещению, представляет работу, совершаемую силой резания, в данном случае силой Pz, в процессе колебаний, которая тратится на дальнейшее развитие колебаний. Сила Ру в таком представлении является упругой силой. В положениях 1, 2 и 3 направление колебаний совпадает с силой Pz, а в положениях 4, 5 и 6 - не совпадает. Величина силы Pz и силы Ру берется на схеме пропорциональной толщине срезаемого слоя, а в каждом положении. Вибрации нарастают до тех пор, пока возрастающие в еще большей степени силы сопротивления или нелинейности другого рода (выход инструмента из контакта с заготовкой; падение минимальной фактической скорости резания до нуля и т. п.) не компенсируют полностью действие энергии, вносимой силой резания. Устанавливаются стабильные колебания — автоколебания с частотой, определяемой свойствами самой колебательной системы и близкой к одной из частот собственных колебаний УС станка. Если фазовый сдвиг между колебаниями таков, что направление движения вершины инструмента будет обратным показанному на рис.1.15, то система будет устойчивой. Изменение силы резания в этих условиях оказывает демпфирующее действие на колебания, вызываемые внешними воздействиями, не пополняя рассеиваемую энергию, как в неустойчивой системе, а, наоборот, увеличивая это рассеивание. Чем больше площадь диаграммы, тем быстрее рассеивается энергия и тем больше степень устойчивости системы, т. е. демпфирование.
Рис.1.15. Траектория относительного движения инструмента и заготовки при автоколебаниях и диаграммы работы сил резания (без учета динамической характеристики резания)
На указанное обстоятельство обращаем особое внимание потому, что отсутствует четкое представление о влиянии резания (в устойчивой системе) на колебания, вызванные внешними возмущениями. При описании процесса резания статической характеристикой изменение демпфирующего эффекта резания определяется не столько резанием, сколько изменениями в конструкции УС, которые определяют направление движения по траектории или, что то же самое, устойчивость системы. Ранее говорилось о том, что поведение замкнутой системы при внешних воздействиях отличается от поведения незамкнутой системы. Описанный эффект влияния резания является одной из иллюстраций этого положения. При упрощенном представлении УС эти условия выражаются невозможностью аппроксимации ее характеристики (в соответствующем диапазоне) уравнением колебательной системы второго порядка. На рис.1.16 показаны следы вибраций на деталях из стали, алюминия, чугуна, текстолита и дерева, динамические свойства процесса резания которых совершенно различны. Эти колебания получены на установке с ориентацией осей жесткости резцедержателя, показанного на рис.1.17.
Рис.1.16. Следы автоколебаний при резании на поверхностях деталей из различных материалов: 1 – текстолит; 2 – сталь; 3 – чугун; 4 – алюминий; 5 – дерево
Перейдем к анализу устойчивости системы с учетом особенностей процесса резания, которые выражаются его динамической характеристикой, определяющей фазовый сдвиг между изменением координаты, в частности, толщины срезаемого слоя и изменением силы резания. В отличие от статической динамическая характеристика резания дает не только изменение масштаба и амплитуд характеристики разомкнутой системы, но дает ей фазовое смещение, поворачивая векторы характеристики УС по часовой стрелке на некоторый угол, как показано на рис.1.14. Амплитудно-фазовая характеристика УС с одной степенью свободы не пересекает отрицательную ветвь вещественной оси. Дополнительное фазовое смещение создает такое пересечение, а следовательно, и условия потери устойчивости, которые определяются тем, что точка пересечения окажется от начала координат далее точки с координатой - 1. В частности, с ростом ширины срезаемого слоя точка пересечения удаляется от начала координат. Можно определить предельную ширину срезаемого слоя, поделив длину отрезка отрицательной ветви вещественной оси на некоторый коэффициент.
Рис.1.17. Экспериментальный резцедержатель
Коэффициент включает, кроме удельной силы резания и жесткости, также постоянные времени резания и УС, выражающие фазовый сдвиг характеристики. Для характеристики резания в форме и характеристики УС в форме отрезок
Этот отрезок имеет наибольшую длину и, следовательно, система наименее устойчива при равенстве постоянной времени резания и инерционной постоянной времени УС. (Это условие получается после приравнивания нулю производной от выражения
Выше было дано, что
Эта зависимость показана на рис.4.6. Минимального значения При этом
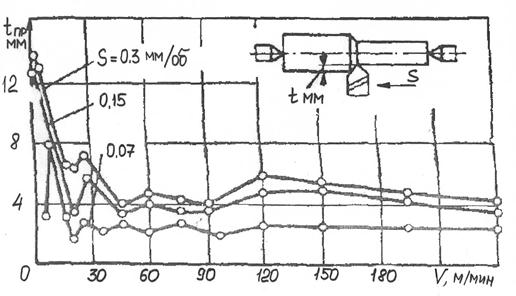
Из приведенных теоретических выражений вытекает еще один метод экспериментального определения постоянной времени резания, кроме указанных в предыдущей главе. Этот метод заключается в том, что по экспериментально полученным кривым предельной ширины срезаемого слоя определяются значения скоростей
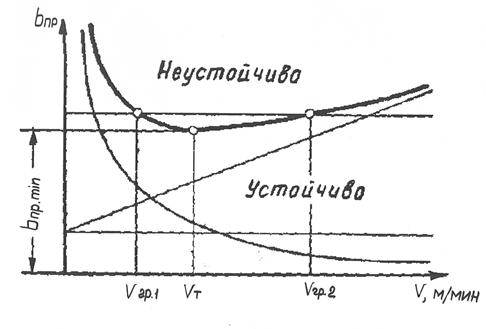
Рис.1.18. Зависимость предельной ширины срезаемого слоя от скорости резания Зная собственную частоту
Этот метод не требует применения сложной аппаратуры и может быть использован в любой лаборатории. Зависимость постоянной времени резания от скорости указывает на возможность существования двух граничных скоростей резания, ниже и выше которых система устойчива и вибрации отсутствуют. Если резание происходит с шириной срезаемого слоя, превышающей
Эти граничные скорости показаны на рис.1.18 для некоторого значения b. Не следует, однако, переоценивать значения того или иного упрощенного выражения динамической характеристики резания в объяснении явления вибраций и его закономерностей. На рис.1.19 приведена зависимость предельной глубины резания от скорости для токарного станка 1К62, полученная экспериментально. Эта зависимость не дает такой четкой зависимости от скорости, какая следует из приведенного теоретического анализа, что может быть следствием влияния наростообразования и вынужденных колебаний на оценку границы устойчивости. Об этом влиянии говорится ниже. В частности, при изменении подачи должно сместиться положение минимума кривой предельной ширины срезаемого слоя по скорости. Однако на кривых рис.1.19 это отчетливо не наблюдается. Наличие двух скоростей — верхней и нижней, ограничивающих область вибраций, известно практикам давно. Большой интерес представляет проверка теоретических результатов, определяемых влиянием динамической характеристики устойчивого резания, при устранении нароста, а также с учетом влияния вынужденных колебаний. Переоценка роли динамической характеристики резания выражается часто в пренебрежении влиянием связанности координат УС, о которой говорилось при анализе системы со стационарным резанием. При этом авторы ограничиваются анализом систем с одной степенью свободы или систем без указанных связей, что не может дать полной картины явления.
Рис.1.19. Зависимость предельной глубины резания от скорости и подачи по экспериментальным данным
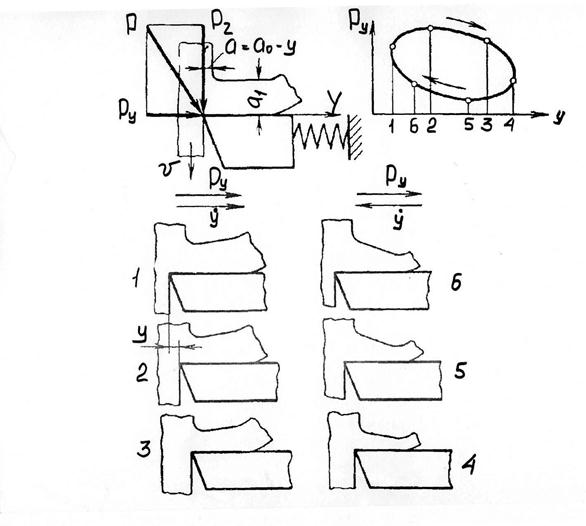
Проведенный анализ показал, что влияние динамической характеристики резания в принципе сводится к дополнительному фазовому смещению в системе. Это обстоятельство очень важно, особенно для УС со слабой связью, когда ее динамическая характеристика не пересекает отрицательной вещественной оси или пересекает ее вблизи от начала координат. Это важно при такой форме характеристик, когда дополнительный фазовый поворот увеличивает отрезок, отсекаемый на отрицательной вещественной оси. При сильной связи форма характеристики может быть иной и ее фазовое смещение мало повлияет на предел устойчивости. Практически это означает, что в такой системе достигнуть существенного эффекта устранения или снижения вибраций за счет изменения скорости резания или подачи нельзя. Необходимо проводить изменения в УС станка, направленные на устранение или изменение соответствующих связей. Более полным и правильным, таким образом, является анализ устойчивости системы как с учетом связей в УС, так и динамической характеристики резания, что и выполняется в данной работе. Отклонения от этого положения и в ту, и в другую стороны, допустимые в соответствующих частных условиях, в общем случае могут привести к ошибочным выводам. Говоря о связанности координат УС, мы имеем в виду прежде всего связанность колебаний, определяющих траекторию относительного движения инструмента и заготовки, а уже потом — другие связи. Остановимся несколько на физической стороне учета динамической характеристике резания в поведении системы. Если при резании, определяемом статической характеристикой, неоднозначное изменение силы резания при колебаниях является следствием особенностей траектории относительного движения инструмента и заготовки и зависимости силы Pz от ортогональной координаты, то в последнем случае эта неоднозначность возникает в результате отставания силы резания от изменения координаты, т.е. от толщины срезаемого слоя. На рис.1.20 показано изменение у толщины срезаемого слоя при колебаниях и соответствующее ему изменение силы Ру резания при наличии указанного отставания. Рассматриваемая УС строго определяется одной степенью свободы (по нормали к поверхности резания). положения 1, 2 и 3 соответствуют отходу резца, а 4, 5 и 6 его внедрению в заготовку, т.е. движению в сторону действия силы Ру резания за один цикл колебания построена на том же рисунке. Площадь, очерченная этой диаграммой, равна работе, идущей на поддержание и развитие колебаний вплоть до установления режима автоколебаний. Описанная физическая картина влияния динамической характеристики резания на устойчивость системы, так же как и выполненные выше построения амплитудно-фазовых характеристик разомкнутой системы, лишний раз показывают, что формы динамической характеристики резания, принимаемые различными исследователями вибраций при резании, отражают один и тот же факт – отставание изменения силы от координаты. Сами характеристики являются различными математическими формами сугубо приближенного описания сложных закономерностей деформации материалов при резании. Основываясь на изложенных общих положениях оценки устойчивости системы при резании, перейдем к рассмотрению отдельных важных сторон этой задачи.
Рис.1.20. Схема изменения толщины стружки и сил резания при смещениях резца (с учетом динамической характеристики резания).
Дата добавления: 2015-01-18 | Просмотры: 846 | Нарушение авторских прав |
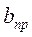 срезаемого слоя, допускаемую системой из условий устойчивости. последнее означает, что отрезок
срезаемого слоя, допускаемую системой из условий устойчивости. последнее означает, что отрезок 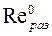 , отсекаемый характеристикой разомкнутой системы на отрицательной вещественной оси, равен единице.
, отсекаемый характеристикой разомкнутой системы на отрицательной вещественной оси, равен единице.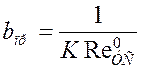 . (1.34)
. (1.34)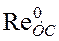 , отсекаемый характеристикой УС на отрицательной ветви вещественной оси, тем меньше предельная ширина срезаемого слоя и ниже виброустойчивость системы.
, отсекаемый характеристикой УС на отрицательной ветви вещественной оси, тем меньше предельная ширина срезаемого слоя и ниже виброустойчивость системы.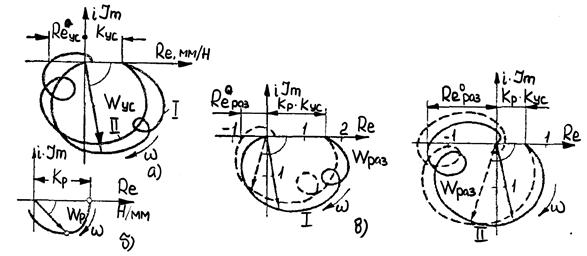
 типов I и II; б – процесса резания
типов I и II; б – процесса резания 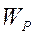 ; в – разомкнутой системы
; в – разомкнутой системы 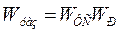 для двух типов УС с учетом статической характеристики резания (сплошная линия) и динамической характеристики резания (штриховая)
для двух типов УС с учетом статической характеристики резания (сплошная линия) и динамической характеристики резания (штриховая)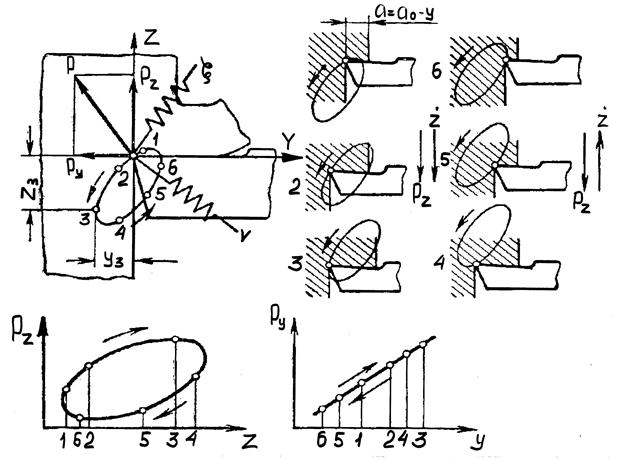

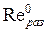 определяется следующим выражением:
определяется следующим выражением: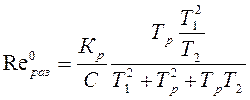 (1.35)
(1.35)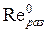 по Тр). Предельная ширина
по Тр). Предельная ширина 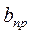 срезаемого слоя определяется из условия
срезаемого слоя определяется из условия 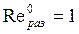 :
: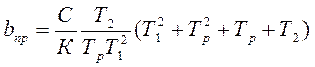 . (1.36)
. (1.36)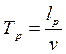 , где
, где 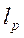 - отрезок пути резания, необходимый для формирования силы резания. подставляя это значение
- отрезок пути резания, необходимый для формирования силы резания. подставляя это значение 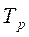 , можно получить выражение для границы устойчивости по скорости или, иначе, зависимость предельной ширины срезаемого слоя от скорости резания:
, можно получить выражение для границы устойчивости по скорости или, иначе, зависимость предельной ширины срезаемого слоя от скорости резания: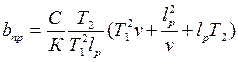 . (1.37)
. (1.37)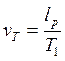 .
.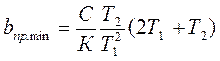 . (1.38)
. (1.38)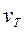 резания, соответствующие минимуму
резания, соответствующие минимуму 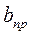 .
.
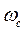 неустойчивой формы колебаний УС, которая приблизительно равна частоте возникающих при резании автоколебаний, находим значение
неустойчивой формы колебаний УС, которая приблизительно равна частоте возникающих при резании автоколебаний, находим значение 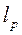 из выражения
из выражения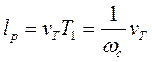 . (1.39)
. (1.39)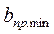 , то эти скорости могут быть вычислены по следующей формуле, получаемой из указанного выше общего уравнения (1.37) границы устойчивости с заменой
, то эти скорости могут быть вычислены по следующей формуле, получаемой из указанного выше общего уравнения (1.37) границы устойчивости с заменой 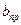 на b и переходом к величине Кр:
на b и переходом к величине Кр: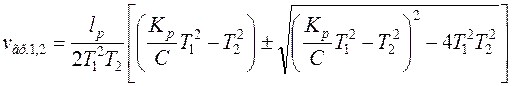 . (1.40)
. (1.40)