 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Изменение энтропии при плавлении твердого тела.Любое изменение состояния тела или системы тел можно представить как результат бесконечно большого числа бесконечно малых изменений. При каждом таком бесконечно малом изменении состояния система либо поглощает, либо выделяет бесконечно малое количество теплоты Количество теплоты, поглощенное или выделенное системой при переходе из одного состояния в другое, зависит от способа перехода и не является функцией состояния. Но если взять отношение теплоты к тем температурам, при которых она были отдана или поглощена, то окажется, что эти величины, так называемые приведенные теплоты, равны между собой:
Эта особенность приведенной теплоты позволяет ввести особую термодинамическую величину – энтропию, имеющую фундаментальное значение в физике. Однозначная функция состояния, полным дифференциалом которой является приведенная теплота
Согласно определению, изменение энтропии при обратимом процессе
Каждое состояние системы характеризуется определенным значением энтропии. В любом замкнутом обратимом процессе изменение энтропии равно нулю:
В термодинамике доказано, что при необратимом процессе энтропия системы возрастает: Подсчитаем изменение энтропии при необратимом процессе плавления твердого тела. Процесс перехода вещества из твердого состояния в жидкое состоит из двух этапов: 1. Нагревание твердого тела от начальной температуры Т 0 до температуры плавления Т пл. При этом
Изменение энтропии на этом этапе
2. Плавление тела. Температура остается постоянной (Т пл=const). Количество теплоты, необходимое для плавления:
Изменение энтропии системы при этом изотермическом процессе
Поскольку энтропия – величина аддитивная, то полное изменение энтропии системы в процессе плавления
Дата добавления: 2015-11-26 | Просмотры: 580 | Нарушение авторских прав |
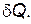
 . (10)
. (10) , называется энтропией:
, называется энтропией: . (11)
. (11)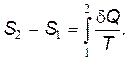 (12)
(12) . (13)
. (13) .
. (14)
(14) (15)
(15) . (16)
. (16) . (17)
. (17) (18)
(18)