 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Вероятностный смысл энтропии
В изолированной системе, как уже говорилось, энтропия возрастает, если происходящие в системе процессы являются необратимыми. С позиции статистической физики, процесс является обратимым, если вероятности осуществления прямого и обратного процессов соизмеримы. Если же обратный процесс маловероятен, то прямой процесс является необратимым. Примером такого процесса является расширение газа в пустоту (самопроизвольное сжатие газа маловероятно). Вероятность процесса будет тем выше, чем больше в результате его существования возрастёт вероятность состояния системы Термодинамической вероятностью системы
где
(5.6.2)
(5.6.3)
С другой стороны, в соответствии с первым началом термодинамики, разделим соотношение
(5.6.4)
Произведя замену с учетом уравнения состояния идеального газа
(5.6.5)
Для обратимого изотермического процесса Но
Отсюда
(5.6.6)
Таким образом, энтропию можно определить (с точностью до константы) в виде
Это - формула Больцмана. Она связывает энтропию с термодинамической вероятностью системы. Чем выше вероятность состояния системы, тем больше энтропия системы. Т.к. в изолированной системе Все процессы в изолированной системе протекают в сторону увеличения вероятности состояния системы. Это статистическое толкование второго начала термодинамики. Из статистики следует что, в относительно малых системах возможны флуктуации, которые могут приводить к кратковременному уменьшению энтропии. Таким образом, 2-е начало не содержит в себе абсолютного запрета убывания энтропии. Другое дело, что на практике для систем с очень большим числом частиц закон неубывания энтропии выполняется без исключений.
Дата добавления: 2015-11-26 | Просмотры: 788 | Нарушение авторских прав 12 |
 (термодинамическая вероятность).
(термодинамическая вероятность). , может быть определено как Ni, тогда термодинамическая вероятность первого состояния определяется выражением
, может быть определено как Ni, тогда термодинамическая вероятность первого состояния определяется выражением (5.6.1)
(5.6.1) – число микросостояний,
– число микросостояний, 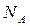 – число Авогадро (т.е. число атомов находящихся в этих состояниях). Считая газ не очень сжатым (т.е.
– число Авогадро (т.е. число атомов находящихся в этих состояниях). Считая газ не очень сжатым (т.е. 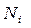 »
» 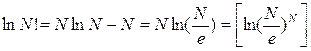
 получим соотношение термодинамических вероятностей для двух различных объёмов газа
получим соотношение термодинамических вероятностей для двух различных объёмов газа  и
и  :
: на T и получим
на T и получим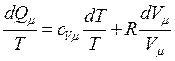
 , получим
, получим
 , и все изменения состояния обусловлены изменением объёма. Тогда
, и все изменения состояния обусловлены изменением объёма. Тогда  и
и 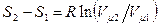
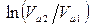 может быть рассчитан, исходя из статистических соображений. Логарифмируя соотношение (5.6.3), связывающее
может быть рассчитан, исходя из статистических соображений. Логарифмируя соотношение (5.6.3), связывающее  и
и  , получим
, получим , или
, или 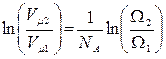
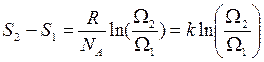
 . (5.6.7)
. (5.6.7) , т.е. S возрастает (по крайней мере, не уменьшается), то это означает, что термодинамическая вероятность в такой системе тоже растёт.
, т.е. S возрастает (по крайней мере, не уменьшается), то это означает, что термодинамическая вероятность в такой системе тоже растёт.