 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Парадокс ГиббсаЭнтропия
Будем снова анализировать обратимый цикл Карно без ограничения на рабочее тело, учитывая эквивалентность термодинамической и идеально-газовой температурных шкал. При этом с учетом замечания о модулях количества теплоты, для кпд цикла Карно имеем
или, снимая модуль,
Отношение количества теплоты к температуре, при которой эта теплота передана, называется приведенным количеством теплоты. Физический смысл выражения (5.4.2) состоит в том, сумма приведенных теплот в цикле Карно равна нулю.
Разобьем цикл адиабатами и соединим их участками изотерм. Таким образом, получим разбиение исходного цикла на
Итак, в обратимом циклическом процессе интеграл по замкнутому контуру от приведенного количества теплоты равен нулю. Из математического анализа известно, что в этом случае под знаком интеграла стоит дифференциал некоторой функции, не зависящей от пути перехода система из одного состояния в другое. Эта функция зависит только от параметров состояния. Функция состояния, дифференциал которой численно равен элементарному приведенному количеству теплоты в обратимом процессе, называет энтропией:
На основании (5.4.3) и термодинамического определения энтропии можно заключить, что в обратимом процессе дифференциально малое приращение энтропии равно нулю
Можно определить и изменение энтропии в обратимом процессе при переходе системы из состояния 1 в состояние 2:
Как вычислить изменение энтропии в необратимом процессе? Поскольку энтропия – функция состояния, ее изменение не зависит от процесса, по которому осуществлен переход. Таким образом, нужно заменить реальный необратимый процесс обратимым с теми же начальным и конечным состояниями и определить изменение энтропии в этом процессе, которое будет равно изменению энтропии при переходе из состояния 1 в состояние 2 необратимым образом. Рассмотрим теперь цикл, включающий неравновесный процесс, то есть необратимый цикл. Предположим, циклический процесс на участке 1-2 необратим, а на участке 2-1 обратим. Как было доказано во второй теореме Карно кпд необратимого цикла всегда меньше кпд обратимого цикла, следовательно
Рассмотрим теперь произвольный необратимый цикл (график процесса не изображаем, так как неравновесное состояние невозможно изобразить на диаграммах состояния: ему не соответствуют значения параметров состояния, относящиеся ко всей системе в целом). Разобьем его на бесконечно малые циклы. Среди этих циклов могут оказаться как равновесные, для каждого из которых приведенное количество теплоты равно нулю, так и неравновесные с приведенной теплотой, меньшей нуля. Таким образом, суммарное количество теплоты за рассматриваемый необратимый цикл меньше нуля.
Объединение условий (5.4.3) и (5.4.8) дает неравенство Клаузиуса для приведенного количества теплоты в циклическом процессе
Знак равенства соответствует обратимому процессу, знак «меньше» - необратимому процессу. Рассмотрим вопрос о направлении процессов в изолированных системах. Пусть изолированная система самопроизвольно перешла из состояния 1 в состояние 2 в результате неравновесного процесса. Для того чтобы осуществить возврат системы в первоначальное состояние (без изменения в окружающих телах) необходимо реализовать равновесный процесс, но для этого придется снять условие изолированности. Тогда интеграл приведенного количества теплоты по замкнутому контуру можно представить в виде суммы двух интегралов, соответствующих приведенному количеству теплоты, переданному изолированной системе в неравновесном процессе и приведенному количеству теплоты, переданному неизолированной системе в равновесном процессе:
Первый интеграл в этой сумме равен нулю, так как система изолирована, и теплота ей не сообщается; второй интеграл, согласно (5.4.6), равен изменению энтропии при переходе из состояния 2 в состояние 1 – (
Итак, энтропия изолированной системы не уменьшается. Она остается неизменной в равновесных процессах и увеличивается в неравновесных:
Выражение (5.4.12) является количественной формулировкой второго начала термодинамики. Как говорилось выше, второе начало термодинамики говорит о направлении процессов в изолированных системах. Известно, что в изолированных системах процессы идут в направлении установления термодинамического равновесия. Таким образом, в равновесии энтропия изолированной системы принимает максимальное значение из всех возможных. Очевидно, что на основании этого факта можно установить микроскопический смысл энтропии. Пока можно изобразить макроскопический критерий эволюции изолированных систем графически (рис.5.4.2). Первое и второе начала термодинамики для равновесных процессов можно объединить в одно выражение – термодинамическое неравенство:
Вне зависимости от свойств термодинамической системы в адиабатном процессе система не обменивается энергией с окружающей средой
и отдается
Тогда для кпд получаем:
где учтены равенства энтропии в состояниях 1 и 4, 2 и 3 соответственно. Таким образом, известное уже соотношение получено путем несколько иных рассуждений. Представление графика процесса в координатах (S,T) позволяет численно определить количество теплоты, переданное или отданное системой в течение процесса. Это количество теплоты численно равно площади под графиком функции T (S) (рис.5.4.4). Из рис. 5.4.3. так же видно, что изменение энтропии рабочего тела равно нулю. Как изменяется при этом энтропия окружающей среды? Изменение энтропии окружающей среды складывается из энтропии отобранной у среды и отданной в среду:
Таким образом, даже обратимая тепловая машина за каждый цикл производит не только работу, но и энтропию. Энтропия системы, включающей рабочее тело и среду, увеличивается. Вычислим изменение энтропии в некоторых квазиравновесных процессах. Рассмотрим квазиравновесные процессы плавления и кристаллизации. Эти процессы можно считать таковыми, если они идут бесконечно медленно, так, что температура системы на бесконечно малую величину отличается от температуры плавления и можно считать, что процесс идет при постоянной температуре. Поэтому можно использовать термодинамическое определение энтропии (5.4.4) и ее изменение определить как
где В (5.4.18) знак «+» соответствует процессу плавления, «‑» - кристаллизации. Таким образом, в процессе кристаллизации энтропия системы уменьшается, однако данный факт не противоречит второму началу термодинамики, поскольку рассматриваемая система не изолирована. Аналогичные результаты можно получить для процессов парообразования и конденсации. При квазиравновесном нагревании без совершения работы изменение энтропии равно:
Найдем общее выражение для определения изменения энтропии идеального газа в обратимом процессе. В термодинамическом тождестве (5.4.13) явно зададим вид дифференциала внутренней энергии идеального газа и уравнение его состояния (1.2.13).
Откуда для дифференциала энтропии получаем
В изотермическом процессе с идеальным газом (5.4.21) упрощается, так как
Когда над идеальным газом производится изохорный процесс, приращение объема равно нулю, при этом изменение энтропии определяется как
Когда изменяется и температура, и давление идеального газа необходимо использовать выражение (5.4.21). Интегрирование последнего выражения приводит к соотношению для вычисления изменения энтропии идеального газа в произвольном обратимом процессе:
Если процесс является изобарным, то
Если обратимый процесс является адиабатным (т.е. dQ= 0), то для него dS= 0 и, значит S=Const. Поэтому адиабатный процесс является изоэнтропийным процессом. Нами уже рассматривалась программа по определению изменения энтропии в необратимом процессе: заменить его обратимым процессом с теми же начальными и конечными состояниями и вычислить изменение энтропии в этом процессе. Рассмотрим использование данной программы на примере необратимого процесса расширения в пустоту идеального газа. Как уже отмечалось, в таком процессе работа не совершается, теплота газу не передается, внутренняя энергия газа остается постоянной, температура не изменяется. Заменим расширение газа в пустоту изотермическим процессом, с теми же начальным и конечным состояниями. Изменение энтропии при обратимом изотермическом процессе, на основании (5.4.22) записывается в виде
В обратимом изотермическом процессе газу передается некоторое количество теплоты, объем увеличивается, и изменение энтропии больше нуля. Изменение энтропии в необратимом, самопроизвольно идущем в одном направлении, процессе расширения газа в пустоту тоже определяется соотношением (5.4.4), а значит больше нуля. Однако система замкнута, так как не обменивается с окружением ни энергией, ни частицами. Таким образом, в необратимом процессе расширения газа в пустоту в замкнутой системе энтропия производилась, генерировалась. Следовательно, энтропия замкнутой системы не сохраняется, в отличие от такой функции состояния как внутренняя энергия. Рассмотрим еще один пример необратимого самопроизвольного процесса: обмен энергией между имеющими разные температуры частями изолированной системы. Пусть для определенности
где учтено, что переданные в обоих направлениях количества теплоты одинаковы по величине и отличаются знаком. Энтропия системы возрастает. Обмен энергией между частями данной системы прекращается, когда их температуры выравниваются, а энтропия достигает максимального значения. Таким образом, пояснена еще одна формулировка второго начала термодинамики: “Самопроизвольно в замкнутой системе термодинамические процессы идут таким образом, что энтропия остается постоянной в обратимых процессах и возрастает в необратимых” (формулировка Больцмана - Планка). Итак, термодинамические процессы даже в замкнутой системе направлены во времени, и необходимо говорить об эволюции такой системы. Второе начало термодинамики в формулировке Больцмана - Планка является критерием эволюции замкнутых систем. В них осуществляется переход от упорядоченного состояния к максимально хаотическому состоянию термодинамического равновесия, в котором энтропия максимальна. Критерий эволюции замкнутых систем графически представлен на рис. 5.4.2 Сформулированный критерий эволюции Больцман применил ко всей Вселенной в целом, тем самым, рассматривая ее как замкнутую систему, и пришел к следующему критерию эволюции Вселенной. Вселенная, как термодинамическая система, эволюционирует к состоянию термодинамического равновесия, то есть к состоянию, в котором отсутствуют распределение температуры, макроскопические потоки. Такое состояние эквивалентно равновесному состоянию идеального газа и было названо тепловой смертью Вселенной. Некоторые факты подтверждают этот вывод, например, скалы разрушаются самопроизвольно, прекратилось вращение Луны вокруг оси, замедляется и вращение Земли вокруг своей оси и т.д. Представления о тепловой смерти Вселенной приводят в мировоззренческий тупик, поскольку в такой эволюции наблюдаемый порядок во Вселенной не может появиться. Как возникло упорядоченное движение планет? Почему в процессе развития общества происходит все большее структурирование? Почему биологическая эволюция на Земле идет в сторону усложнения структур? Кто-то создал порядок, дал толчок эволюции? Современная термодинамика нашла ответы на эти вопросы, и к их рассмотрению мы еще обратимся, а пока проанализируем другой парадокс, следующий из второго начала термодинамики.
Парадокс Гиббса
Вновь рассмотрим сосуд объемом V, разделенный перегородкой на две части, но пусть теперь они заполнены разными газами, находящимися в состоянии термодинамического равновесия, между которыми тоже существует термодинамическое равновесие, то есть температуры и давления в обеих частях сосуда одинаковы. Если убрать перегородку, происходит диффузия до нового равновесного состояния, в котором распределение молекул обоих газов равномерно, так как предполагается отсутствие внешних полей. Рассчитаем изменение энтропии в этом процессе. Данный процесс можно рассматривать как расширение в пустоту каждого из двух газов, и изменение энтропии определить как сумму изменений энтропии в каждом из этой процессов:
Очевидно, изменение энтропии в анализируемом процессе больше нуля. Состояние в сосуде с перегородкой более упорядоченное, по сравнению с конечным состоянием. Самостоятельно смесь не делится на две компоненты, то есть процесс необратим. Происходит уменьшение упорядоченности, увеличение беспорядка, при этом энтропия возрастает.
Таким образом, возникает парадокс: при самодиффузии энтропия не изменяется, при взаимной диффузии - возрастает. Если устремить массу молекулы первого газа к массе молекулы второго, тогда при непрерывном уменьшении разности масс Дата добавления: 2015-11-26 | Просмотры: 772 | Нарушение авторских прав 12 |
 , (5.4.1)
, (5.4.1) . (5.4.2)
. (5.4.2) Рассмотрим теперь произвольный обратимый цикл (рис. 5.4.1).
Рассмотрим теперь произвольный обратимый цикл (рис. 5.4.1). циклов Карно. Теперь, чтобы найти приведенное количество теплоты, нужно сложить приведенные количества теплот в этих циклах. Чем чаще проводятся адиабаты, тем ближе сумма
циклов Карно. Теперь, чтобы найти приведенное количество теплоты, нужно сложить приведенные количества теплот в этих циклах. Чем чаще проводятся адиабаты, тем ближе сумма 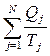 к значению приведенного количества теплоты в рассматриваемом цикле. В переделе бесконечно близких адиабат суммарное приведенное количество теплоты равно интегралу элементарного приведенного количества теплоты
к значению приведенного количества теплоты в рассматриваемом цикле. В переделе бесконечно близких адиабат суммарное приведенное количество теплоты равно интегралу элементарного приведенного количества теплоты  по замкнутому контуру. Так как в каждом из циклов Карно приведенное количество теплоты равно нулю, то и указанный интеграл равен нулю:
по замкнутому контуру. Так как в каждом из циклов Карно приведенное количество теплоты равно нулю, то и указанный интеграл равен нулю: . (5.4.3)
. (5.4.3) . (5.4.4)
. (5.4.4) . (5.4.5)
. (5.4.5) . (5.4.6)
. (5.4.6) . Значит сумма приведенных теплот в случае необратимого цикла, при температурах нагревателя и холодильника
. Значит сумма приведенных теплот в случае необратимого цикла, при температурах нагревателя и холодильника  и
и  соответственно, меньше нуля:
соответственно, меньше нуля: . (5.4.7)
. (5.4.7) (5.4.8)
(5.4.8) . (5.4.9)
. (5.4.9) (5.4.10)
(5.4.10) ). Весь интеграл по замкнутому контуру 121, согласно неравенству Клаузиуса (5.4.8), меньше нуля, так как один из процессов, образующих цикл, необратим. Следовательно,
). Весь интеграл по замкнутому контуру 121, согласно неравенству Клаузиуса (5.4.8), меньше нуля, так как один из процессов, образующих цикл, необратим. Следовательно, . (5.4.11)
. (5.4.11)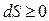 (5.4.12)
(5.4.12) . (5.4.13)
. (5.4.13) В виде тождества оно справедливо для равновесных процессов в любых термодинамических системах, так как в нем не использовано никаких параметров конкретных моделей системы. Знак неравенства соответствует соотношению между термодинамическими величинами в неравновесных процессах в различных системах.
В виде тождества оно справедливо для равновесных процессов в любых термодинамических системах, так как в нем не использовано никаких параметров конкретных моделей системы. Знак неравенства соответствует соотношению между термодинамическими величинами в неравновесных процессах в различных системах. , следовательно, и дифференциал энтропии в этом процессе равен нулю (по определению 5.4.4). В адиабатном процессе энтропия сохраняется, и этот процесс можно рассматривать как изоэнтропийный. Идеальный цикл удобно изобразить в координатах (S,T), как это сделано на рис.5.4.3.
, следовательно, и дифференциал энтропии в этом процессе равен нулю (по определению 5.4.4). В адиабатном процессе энтропия сохраняется, и этот процесс можно рассматривать как изоэнтропийный. Идеальный цикл удобно изобразить в координатах (S,T), как это сделано на рис.5.4.3. Вычислим коэффициент полезного действия идеальной машины Карно. Теплота
Вычислим коэффициент полезного действия идеальной машины Карно. Теплота  сообщается на участке 1-2
сообщается на участке 1-2 (5.4.14)
(5.4.14) на изотерме 3-4:
на изотерме 3-4: . (5.4.15)
. (5.4.15) ,(5.4.16)
,(5.4.16)
 . (5.4.17)
. (5.4.17) , (5.4.18)
, (5.4.18)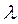 - удельная теплота кристаллизации.
- удельная теплота кристаллизации. . (5.4.19)
. (5.4.19) . (5.4.20)
. (5.4.20) . (5.4.21)
. (5.4.21) и изменение энтропии определяется выражением
и изменение энтропии определяется выражением . (5.4.22)
. (5.4.22) (5.4.23)
(5.4.23) . (5.4.24)
. (5.4.24) и
и . (5.4.25)
. (5.4.25) . (5.4.26)
. (5.4.26) . Изменение энтропии системы складывается в этом процессе из изменения энтропии каждой части:
. Изменение энтропии системы складывается в этом процессе из изменения энтропии каждой части: , (5.4.27)
, (5.4.27) . (5.5.1)
. (5.5.1) Данный опыт можно произвести и с одним газом в обеих частях, при этом будет наблюдаться самодиффузия. Как изменится энтропия в этом случае? Объективных данных для различия состояний при протекании самодиффузии нет, следовательно, энтропия в этом случае не изменяется (рис. 5.5.1).
Данный опыт можно произвести и с одним газом в обеих частях, при этом будет наблюдаться самодиффузия. Как изменится энтропия в этом случае? Объективных данных для различия состояний при протекании самодиффузии нет, следовательно, энтропия в этом случае не изменяется (рис. 5.5.1). , изменение энтропии осуществляется скачком. Этот парадокс был сформулирован Гиббсом, но просуществовал недолго. Данный парадокс был разрешен квантовой физикой. Параметры молекулы, как и любых других квантовых объектов, отличаются друг от друга на конечную величину. Таким образом, парадокса нет, так как непрерывное изменение параметров молекул невозможно.
, изменение энтропии осуществляется скачком. Этот парадокс был сформулирован Гиббсом, но просуществовал недолго. Данный парадокс был разрешен квантовой физикой. Параметры молекулы, как и любых других квантовых объектов, отличаются друг от друга на конечную величину. Таким образом, парадокса нет, так как непрерывное изменение параметров молекул невозможно.