 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
для интенсивных и экстенсивных показателей, исключая показатель инцидентности «человек-время).
m – стандартная ошибка, имеющая ту же размерность, что и показатель П; П– относительный показатель, выраженный в необходимой размерности, а именно: · показатель инцидентности (заболеваемости) (I); · показатели превалентности (PRM, PRP); · экстенсивный показатель (Р), q – разность между размерностью показателя и его величиной: q = 1 –П, если П выражен в долях единицы; q = 100 –П, если П выражен в процентах (0/0); q = 1000 – П, если П выражен в промилле (0/00); q = 10000 – П, если П выражен в продецимилле (0/000); q = 100000 – П, если П выражен в просантимилле (0/0000); N для интенсивных показателей: это, численность населения, использованная в расчёте данного показателя заболеваемости, N для экстенсивных показателей: – это суммарное число больных, составляющих данное структурное распределение, т.е знаменатель формулы расчета экстенсивных показателей. 2. для показателя человек-время (PtR), (плотности инцидентности) m PtR - – стандартная ошибка, имеющая ту же размерность, что и показатель PtR PtR – показатель человек-время (показатель плотности инцидентности) ЧЧЛ - число человеко-лет, т.е. значение знаменателя в формуле PtR. Обратите внимание, (табл. 8) что величина стандартной ошибки, существенно зависит от численности населения – при одинаковом значении показателей, чем меньше N, тем больше стандартные ошибки этих показателей.
Табл.8. Заболеваемость краснухой населения РФ и условных городов А, Б, В и Г в 2001 году (А.- число выявленных случаев краснухи, I0/0000, m- стандартная ошибка показателя). Численность населения условных территорий (гор. А, Б, В и Г) постепенно уменьшается, поэтому стандартная ошибка (m), несмотря на одинаковой показатель заболеваемости, постоянно и существенно увеличивается. Оценка достоверности различий показателей заболеваемости с помощью критерия t. Критерий t – это критерий статистической значимости (достоверности) или доверительный коэффициент. Критерий t рассчитывается по общей формуле:
П1 и П2 – два любых относительных показателя, а именно: · показатели инцидентности (заболеваемости) (I); · показатели превалентности (PRM, PRP); · экстенсивные показатели (Р); ·показатели человек-время (PtR)); m1 и m2 – стандартные ошибки сравниваемых показателей. Как оценить величину критерия t? Значения критерия t взаимосвязано с уровнем доверия (P) Это значит, что определённому значению t соответствует только одно значение уровня (P). И наоборот, каждому значению уровня доверия (P) соответствует строго определённое значение критерия t. При этом чем больше значение критерия t, тем больше значение уровня доверия (Р) и, соответственно, меньше уровень ошибки (р). Так, при числе N больше 30: · t = 0,675 соответствует значению P =0,50, и р =0,5 · t = 1,0 соответствует значению Р =0,6827; и р =0,3173 · t = 1,8 соответствует значению Р =0,9281; и р =0,0719 · t = 1,90 соответствует значению Р =0,9425; и р =0,0575 · t = 1,96 соответствует значению Р=0,95; и р =0,05 · t = 3,0 соответствует значению P =0,9973 и р =0,0027, · Самое высокое значение Р=0,9997, и р= 0,0003, (следовательно, ошибка составляет всего 0,03%), соответствует t =3,58. Дальнейшее увеличение значения t не изменяет значения Р или р. Все значения уровня достоверности Р, соответствующие различным значениям t, можно найти в приложении любого статистического справочника. При оценке разницы показателей, например I1 и I2 принято считать, что: · если значение критерия tменьше 1,96 то, следовательно, показатели Р1 и Р2 различаются с уровнем доверия меньшим, чем 0,95 (P<0,95), а ошибка соответственно, больше 0,05 (р>0,05). В этом случае различие сравниваемых показателей признается статистически недостоверным, несущественным, обусловленным действием случайных факторов; · если значение критерия tравно, или больше 1,96 то это означает, что показатели Р1 и Р2 различаются с уровнем доверия равным или большим, чем 0,95 (P>0,95) а, значение ошибки р<0,05. Такое различие показателей I1 и I2 признаётся статистически достоверным, неслучайным. Внимание! Вывод о статистической достоверности различий еще не указывает, какова абсолютная и относительная выраженность различий показателей. Этот уровень доверия позволяет лишь (с известной долей ошибки) утверждать, что различие показателей не случайно, а обусловлено разной активностью ( набором ) объективных и (или) субъективных причин, определивших значения сравниваемых показателей. При этом, если значение критерия t соответствует величине ошибки значительно меньшей, чем р <0,05, то рекомендуется привести точное значение р, или хотя бы указывать, что оно меньше 0,01 (для этого значения р критическая величина t =2,58). Такой прием уточняет, на сколько полученный результат измерения ошибки достоверности различий меньше принятой «точки отсечки - точки р =0,05». Точно также если уровень ошибки больше 0,05, рекомендуется указать его точное значение, что бы читатель мог сам решить, как относиться к результатам исследования. Например, если в результате оценки достоверности различий каких-либо величин получен критерий t = 5,6, то не следует ориентироваться на критические величины и обозначать ошибку как р<0,05. По крайней мере необходимо указать, что р< 0,001, такое значение ошибки существенно увеличит уверенность читателя в том, что полученные в исследовании результаты не случайны. Или, если например получено значение t= 1,90, более правильным будет указать точное значение ошибки, т.е. р=0,0575, а не ограничится указанием, что р>0,05, ведь в данном случае результаты исследования совсем немного не «дотягивают» до критической точки, позволяющей отвергнуть нулевую гипотезу с 5% ошибкой. Оценка достоверности различий показателей заболеваемости с помощью доверительных границ (интервалов). С учётом высказанного ранее допущения о вероятностной природе показателя заболеваемости, доверительные границы определяют доверительный интервал случайных колебаний показателя и, следовательно, определяют границы, в которых может находиться истинный показатель заболеваемости, или другие эпидемиологические переменные (если не было систематической ошибки) Существуют нижние (НДГ) и верхние (ВДГ) доверительные границы сравниваемых показателей заболеваемости. НДГ рассчитывается по формуле П - tm, ВДГ рассчитывается по формуле П+ tm, Общая формула расчета: НДГ (ВДГ) = П ± tm где: П– интенсивный (I) или экстенсивный (Р) показатель к которому рассчитывается НДГ и ВДГ m – стандартная ошибка этого показателя t - критерий достоверности Следует подчеркнуть, что доверительные границы показателя заболеваемости рассчитываются для заранее выбранного уровня доверия. При этом критерий t показывает, сколько стандартных ошибок (m) необходимо отнять от показателя или прибавить к нему, чтобы получить соответственно НДГ и ВДГ для выбранного уровня доверия.
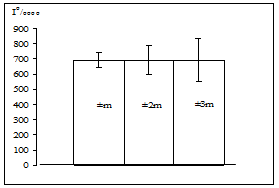
Рис.7 Заболеваемость коклюшем детей до 14 лет в г. В. в 2000 г. (доверительные границы показателя I 0/00000 рассчитаны с разными уровнями доверия: I±m, I±2m, I±3m) Рис. 7 наглядно показывает, что чем строже выбранный уровень доверия, тем шире доверительный интервал одного и того же показателя. Таким образом, чем ниже уровень доверия, тем меньше доверительные границы к одному и тому же показателю. В данном случае, т.е. при применении статистики нормального распределения показатель заболеваемости (для которого рассчитывались НДГ и ВДГ) находится в центре доверительного интервала (рис. 7). При применении статистики Пуассона НДГ и ВДГ не равны друг другу. Поскольку в медицине, в качестве пограничной величины разделяющей различия на достоверные и мало достоверные используется Р =0,95 (р =0,05), которым соответствует t =1,96, доверительный интервал рассчитывается как П ± 1.96m или приблизительно как П ± 2m. «Метод доверительных границ» применяют, главным образом, для наглядного отображения достоверности различий сравниваемых величинна линейных или столбиковых диаграммах. Без нанесения на такие диаграммы доверительных границ показателей заболеваемости трудно, а чаще всего невозможно (если не использовались другие методы) делать уверенные заключения, например, об особенностях динамики, или структуры заболеваемости. В этих случаях все выводы носят предварительный (ориентировочный) характер и требуют дальнейшего уточнения. Несмотря на высокую наглядность «метод доверительных границ» в некоторых случаях (см. далее) не позволяет высказать уверенные суждения об уровне доверия (ошибки) наблюдаемых различий. В таких случаях необходима дополнительная оценка уровня доверия (ошибки) с помощью критерия t. Как же определить достоверность различий показателей заболеваемости, используя «метод доверительных границ»? Для этого необходимо рассчитать, нанести на диаграмму и сравнить доверительные интервалы соответствующих показателей заболеваемости используя формулу НДГ(ВДГ) = П±2m. Сравнение доверительных границ заключается, прежде всего, в выявлении отсутствия или наличия трансгрессии то есть явления неполного разобщения (перекрытия) доверительных интервалов сравниваемых показателей. При сравнении доверительных интервалов возможны следующие варианты.
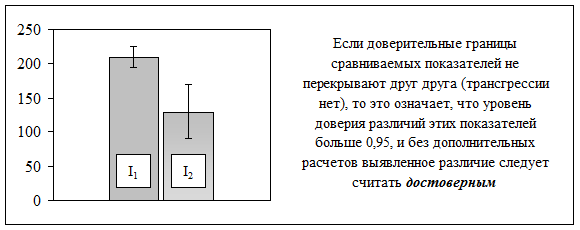
Рис.8. Трансгрессии нет
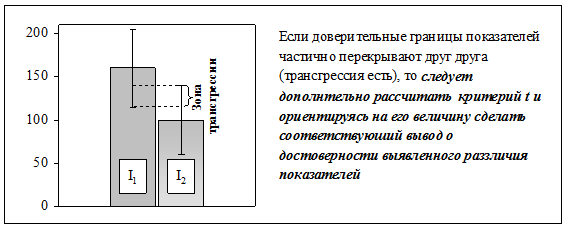
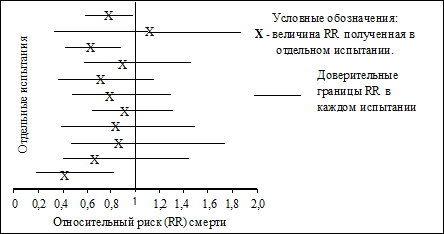
Рис.9 Трансгрессия есть. Расчет и сравнение доверительных границ используется не только в описательных, но также часто и в аналитических исследования. Так, например, доверительные интервалы величин, полученных в нескольких исследованиях, посвященных изучению одной проблемы, позволяют читателю увидеть разброс данных в отдельных исследованиях, и сделать соответствующие выводы об их точности. В силу особой наглядности, сравнение на рисунках доверительных интервалов, вместо традиционного расчета величины р, особенно широкостало использоваться в клинической эпидемиологии при отражении результатов рандомизированных клинических испытаний всего того, что используется в клинической практике для диагностики и лечения больных. Данные, полученные в таких испытаниях, являются основой научно обоснованной клинической практики (доказательной медицины). Так на рис. 10 хорошо видно, что в разных испытаниях и значения относительных рисков смерти при применении бета–блокаторов и доверительные интервалы полученных значений относительного риска (RR) существенно различаются. Наиболее вероятная причина широких доверительных интервалов – проведение исследования на небольших выборках.
Рис. 7.4. Результаты серии независимых рандомизированных испытаний В заключение ещё раз подчеркнём, что оценка уровня достоверности (уровня ошибки) различий показателей заболеваемости является основным и обязательным элементом статистической обработки эпидемиологических данных. Без такой оценки неправомерно делать уверенные выводы об эпидемиологической значимости различий показателей заболеваемости, делать заключения об особенностях динамики и структуры заболеваемости и выдвигать гипотезы о факторах риска и оценивать результаты экспериментальных исследований. Однако, к сожалению, несмотря на вышесказанное, до настоящего времени в различных статьях, диссертациях, учебниках, отчётах (даже государственных) весьма часто сравнение показателей и формирование выводов происходит без оценки уровня доверия (ошибки) наблюдаемых различий. Всё это свидетельствует о недостаточной культуре анализа эпидемиологических данных. Дата добавления: 2015-12-15 | Просмотры: 769 | Нарушение авторских прав |
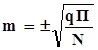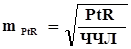где:
где: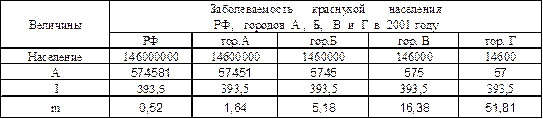
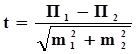(Знак разности не учитывается) где:
