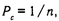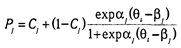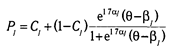|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Бланк методики «Культурно-ценностный дифференциал» 4 страницаЕсли топология свойства не определена, то это означает, что множество испытуемых нельзя (в соответствии с определением понятия «свойство») разбить на подмножества, обладающие или не обладающие свойством. Иначе: на множестве испытуемых нельзя ввести отношения эквивалентности—неэквивалентности. Однако на множестве испытуемых можно ввести отношения толерантности (сходства). Это отношение рефлексивно, симметрично, но не транзитивно. Множество индикаторов Единственно возможный способ интерпретации таких результатов — выделение из множества испытуемых «эталонного испытуемого» (например, решившего все задачи теста). После этого производится подсчет коэффициентов сходства всех испытуемых с «эталоном». Назовем этот вариант модели «моделью сходств». В психологических исследованиях она применяется редко. Очевидно, свою роль играет стремление исследователей максимально повысить мощность интерпретации данных. 2. Свойство качественно определено. Топология свойства определена: оно является точечным. На множества испытуемых можно ввести отношение эквивалентности—неэквивалентности (рефлексивное, симметричное, транзитивное), указывающее на наличие или отсутствие у них свойства. Следовательно, отображение F 1: Назовем эту модель моделью дихотомической классификации. Она использована в опросниках Личко, опросниках УНП и ряде других. 3. Свойство качественно и количественно определено. Свойство является линейным континуумом, следователь, на нем определена метрика. Отображение F 1': В этом случае для подсчета величины, характеризующей принадлежность испытуемого к определенной интенсивности свойства, применяют кумулятивно-аддитивную модель: число признаков, проявленных при выполнении заданий теста (с учетом «весов»), прямо пропорционально интенсивности свойства, которым обладает испытуемый. Эта модель есть отображение F2': Индикаторы свойства также могут быть однородными и разнородными. В последнем случае они шкалируются или не шкалируются. Если индикаторы однородны, то они выявляют свойство или уровень его интенсивности с равной вероятностью. Если индикаторы разнородны, то они выявляют свойство или уровень его интенсивности с разной вероятностью. На множестве индикаторов может быть введена некоторая мера — «сила» признака: чем сильнее признак, тем с большей вероятностью он выявляет свойство или определенный уровень его интенсивности. В этом случае для описания теста мы получаем так называемую модель Раша. 6.4. Классическая эмпирико-статистическая теория теста Классическая теория теста лежит в основе современной дифференциальной психометрики. Описание оснований этой теории содержится во многих учебниках, пособиях, практических руководствах, научных монографиях. Количество изданных учебников, излагающих эмпирико-статистическую теорию теста, особенно выросло за последние 5-7 лет. Вместе с тем в учебнике, посвященном методам психологического исследования, нельзя хотя бы вкратце не упомянуть основные положения теории психологического тестирования. Конструирование тестов для изменения психологических свойств и состояний основано на шкале интервалов. Измеряемое психическое свойство считается линейным и одномерным. Предполагается также, что распределение совокупности людей, обладающих данным свойством, описывается кривой нормального распределения. В основе тестирования лежит классическая теория погрешности измерений; она полностью заимствована из физики. Считается, что тест — такой же измерительный прибор, как вольтметр, термометр или барометр, и результаты, которые он показывает, зависят от величины свойства у испытуемого, а также от самой процедуры измерения («качества» прибора, действий экспериментатора, внешних помех и т.д.). Любое свойство личности имеет «истинный» показатель, а показания по тесту отклоняются от истинного на величину случайной погрешности. На показания теста влияет и «систематическая» погрешность, но она сводится к прибавлению (вычитанию) константы к «истинной» величине параметра, что для интервальной шкалы значения не имеет. Если тест проводить много раз, то среднее будет характеристикой «истинной» величины параметра. Отсюда выводится понятие ретестовой надежности: чем теснее коррелируют результаты начального и повторного проведения теста, тем он надежнее. Стандартная погрешность измерения:
Предполагается, что существует множество заданий, которые могут репрезентировать измеряемое свойство Тест есть лишь выборка заданий из их генеральной совокупности. В идеале можно создать сколько угодно эквивалентных форм теста. Отсюда — определение надежности теста методами параллельных форм и расщепление его на эквивалентные равные части. Задания теста должны измерять «истинное» значение свойства. Все задания одинаково скоррелированы друг с другом. Корреляция задания с истинным показателем:
Поскольку в реальном монометрическом тесте число заданий ограничено (не более 100), то оценка надежности теста всегда приблизительна. Так, определяемая надежность теста связана с однородностью, которая выражается в корреляциях между заданиями. Надежность возрастает с увеличением одномерности теста и числа его заданий, причем довольно быстро. Стандартная надежность 0,02 соответствует тесту длиной в 10 заданий, а при 30 заданиях она равна 0,007. Оценка стандартной надежности:
Для оценок надежности используется ряд показателей. Наиболее известна формула Кронбаха:
Для определения надежности методом расщепления используется формула Спирмена—Брауна. В принципе классическая теория теста касается лишь проблемы надежности. Вся она базируется на том, что результаты выполнения разных заданий можно суммировать с учетом весовых коэффициентов. Так получается «сырой» балл Y=åaxi+c, где xi — результат выполнения i -го задания, а — весовой коэффициент ответа, с — произвольная константа. По поводу того, откуда возникают «ответы», в классической теории не говорится ни слова. Несмотря на то, что проблеме валидности в классической теории теста уделяется много внимания, теоретически она никак не решается. Приоритет отдан надежности, что и выражено в правиле: валидность теста не может быть больше его надежности. Валидность означает пригодность теста измерять то свойство, для измерения которого он предназначен. Следовательно, чем больше на результат выполнения теста или отдельного задания влияет измеряемое свойство и чем меньше — другие переменные (в том числе внешние), тем тест валидней и, добавим, надежнее, поскольку влияние помех на деятельность испытуемого, измеряемую валидным тестом, минимально. Но это противоречит классической теории теста, которая основана не на дея-тельностном подходе к измерению психических свойств, а на бихевиористской парадигме: стимул—ответ. Если же рассматривать тестирование как активное порождение испытуемым ответов на задания, то надежность теста будет функцией, производной от валидности. Тест валиден (и надежен), если на его результаты влияет лишь измеряемое свойство. Тест невалиден (и ненадежен), если результаты тестирования определяются влиянием нерелевантных переменных. Каким же образом определяется валидность? Все многочисленные способы доказательства валидности теста называются разными ее видами. 1. Очевидная валидность. Тест считается валидным, если у испытуемого складывается впечатление, что он измеряет то, что должен измерять. 2. Конкретная валидность, или конвергентная—дивергентная валидность. Тест должен хорошо коррелировать с тестами, измеряющими конкретное свойство либо близкое ему по содержанию, и иметь низкие корреляции с тестами, измеряющими заведомо иные свойства. 3. Прогностическая валидность. Тест должен коррелировать с отдаленными по времени внешними критериями: измерение интеллекта в детстве должно предсказывать будущие профессиональные успехи. 4. Содержательная валидность. Применяется для тестов достижений: тест должен охватывать всю область изучаемого поведения. 5. Конструктная валидность. Предполагает: а) полное описание измеряемой переменной; б) выдвижение системы гипотез о связях ее с другими переменными; в) эмпирическое подтверждение (неопровержение) этих гипотез. С теоретической точки зрения, единственным способом установления «внутренней» валидности теста и отдельных заданий является метод факторного анализа (и аналогичные), позволяющий: а) выявлять латентные свойства и вычислять значение «факторных нагрузок» — коэффициенты детерминации свойств тех или иных поведенческих признаков; б) определять меру влияния каждого латентного свойства на результаты тестирования. К сожалению, в классической теории теста не выявлены причинные связи факторных нагрузок и надежности теста. Дискриминативность задания является еще одним параметром, внутренне присущим тесту. Тест должен хорошо «различать» испытуемых с разными уровнями выраженности свойства. Считается, что больше 9-10 градаций использовать не стоит. Тестовые нормы, полученные в ходе стандартизации, представляют собой систему шкал с характеристиками распределения тестового балла для различных выборок. Они не являются «внутренним» свойством теста, а лишь облегчают его практическое применение. 6.5. Стохастическая теория тестов (IRT) Наиболее общая теория конструирования тестов, опирающаяся на теорию измерения, — Item Response Theory (IRT). Она основывается на теории латентно-структурного анализа (ЛСА), созданной П. Лазарсфельдом и его последователями. Латентно-структурный анализ создан для измерения латентных (в том числе психических) свойств личности. Он является одним из вариантов многомерного анализа данных, к которым принадлежат факторный анализ в его различных модификациях, многомерное шкалирование, кластерный анализ и др. Теория измерения латентных черт предполагает, что: 1. Существует одномерный континуум свойства — латентной переменной (х); на этом континууме происходит вероятностное распределение индивидов с определенной плотностью f(х). 2. Существует вероятностная зависимость ответа испытуемого на задачу (пункт теста) от уровня его психического свойства, которая называется характеристикой кривой пункта. Если ответ имеет две градации («да — нет», «верно — неверно»), то эта функция есть вероятность ответа, зависящая от места, занимаемого индивидом на континууме (х).
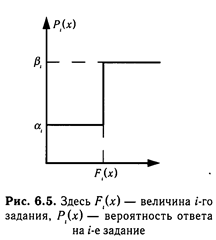
3. Ответы испытуемого не зависят друг от друга, а связаны только через латентную черту. Вероятность того, что, выполняя тест, испытуемый даст определенную последовательность ответов, равна произведению вероятностей ответов на отдельные задания. Конкретные модели ЛСА, применяемые для анализа эмпирических данных, основаны на дополнительных допущениях о плотности распределения индивидов на латентном континууме или о форме функциональной связи уровня выраженности свойства у испытуемого и ответа на пункт теста. В модели латентного класса функция плотности распределения индивидов является точечно-дискретной: все индивиды относятся к разным непересекающимся классам. Измерение производится при помощи номинальной шкалы. В модели латентной дистанции постулируется, что вероятность ответа индивида на пункт текста является мультипликативной функцией от параметров задачи и величины свойства:
Вероятность ответа на пункт теста описывается функцией, изображенной на графике (рис. 6.5). Модель нормальной огивы есть обобщение модели латентной дистанции. В ней вероятность ответа на задание такова:
В логистической модели вероятность ответа на задание описывается следующей зависимостью:
Логистическая модель используется наиболее широко, так как она специально предназначена для тестов, где свойство измеряется суммированием баллов, полученных за выполнение каждого задания с учетом их весов. Логистическая функция и функция нормального распределения тесно связаны:
Развитием ЛСА являются различные модификации Item Response Theory. В IRT распределения переменных на оси латентного свойства непрерывны, т.е. модель латентного класса не используется. База для IRT— это модель латентной дистанции. Предполагается, что и индивидов, и задания можно расположить на одной оси «способность — трудность» или «интенсивность свойства — сила пункта». Каждому испытуемому ставится в соответствие только одно значение латентного параметра («способности»). В общем виде вероятность ответа зависит от множества свойств испытуемого, но в моделях IRT рассматривается лишь одномерный случай. Главное отличие IRT от классической теории теста в том, что в ней не ставятся и не решаются фундаментальные проблемы эмпирической валидности и надежности теста: задача априорно соотносится лишь с одним свойством, т.е. тест заранее считается валидным. Вся процедура сводится к получению оценок параметров трудности задания и к измерению «способностей» испытуемых (образованию «характеристических кривых»). В классической теории теста индивидуальный балл (уровень свойства) считается некоторым постоянным значением. В IRT латентный параметр трактуется как непрерывная переменная. Первичной моделью в IRT стала модель латентной дистанции, предложенная Г. Рашем: [Rasch G., 1980]: разность уровня способности и трудности теста xi – bi, где хi — положение i -ro испытуемого на шкале, а bj — положение j -го задания на той же шкале. Расстояние (xi – bi) характеризует отставание способности испытуемого от уровня сложности задания. Если разница велика и отрицательна, то задание не может быть выполнено, так как для данного испытуемого оно слишком сложно. Если же разница велика и положительна, то задание также не информативно, ибо испытуемый заведомо легко и правильно его решит. Вероятность правильного решения задания (или ответа «да») i -м испытуемым:
Вероятность выполнения j -го задания группой испытуемых:
В IRT функции х и f(b) называются функциями выбора пункта. Соответственно первая является характеристической функцией испытуемого, а вторая — характеристической функцией задания. Считается, что латентные переменные х и b нормально распределены, поэтому для характеристически функций выбирают либо логистическую функцию, либо интегральную функцию нормированного нормального распределения (как мы уже отметили выше, они мало отличаются друг от друга). Поскольку логистическую функцию проще аналитически задавать, ее используют чаще, чем функцию нормального распределения. Кроме «свойства» и «силы пункта» (она же — трудность задания) в аналитическую модель IRT могут включаться и другие переменные. Все варианты IRT классифицируются по числу используемых в них переменных. Наиболее известны однопараметрическая модель Г. Раша, двухпараметрическая модель А. Бирнбаума и его же трехпараметрическая модель. В однопараметрической модели Раша предполагается, что ответ испытуемого обусловлен только индивидуальной величиной измеряемого свойства (qi) и «силой» тестового задания (bj). Следовательно, для верного ответа («да»)
и для неверного ответа («нет»)
Наиболее распространена модель Раша с логистической функцией отклика.
Для тестового задания:
Для испытуемого:
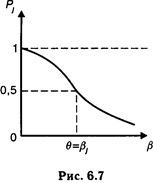
Естественно, чем выше уровень свойства (способности), тем вероятнее получить правильный ответ («ключевой» ответ — «да»). Следовательно, функция В точке перегиба характеристической кривой i-го задания теста «способность» равна «трудности задания», следовательно, «вероятность его решения» равна 0,5 (рис. 6.6). Очевидно, что индивидуальная кривая испытуемого, характеризующая вероятность решить то или иное задание (дать ответ «да»), будет монотонно убывающей функцией(рис. 6.7). В точке на шкале, где «трудность» равна «индивидуальной способности испытуемого», происходит перегиб функции. С ростом «способности» (развитием психологического свойства) кривая сдвигается вправо. Главной задачей IRT является шкалирование пунктов теста и испытуемых. Упростим исходную формулу модели, введя параметр V = e qi-bi:
Шанс на успех i -го испытуемого при решении j -го задания определяется отношением:
Если сравнить шансы двух испытуемых решить одно и то же j -е задание, то это отношение будет следующим:
Следовательно, разница в успешности задания испытуемыми не зависит от сложности задания и определяется лишь уровнем способности. Нетрудно заметить, что в модели Раша отношение трудности заданий не зависит от способности испытуемых. Для того чтобы убедиться в этом, достаточно проделать аналогичные простейшие преобразования, сравнивая вероятности ответов группы на два пункта теста, а не вероятности ответов разных испытуемых.
Следовательно,
Для сравнения шансов на успех i -го испытуемого решить задания k и п берем отношение:
Тем самым отношение шансов испытуемого решить два разных задания определяется лишь трудностью этих заданий. Обратим внимание, что шкала Раша (в теории) является шкалой отношений. Теперь у нас есть возможность ввести единицу измерения способности (в общем виде — свойства). Если взять натуральный логарифм от e bn – bk или е qi – qm, то получается единица измерения «логит» (термин ввел Г. Раш), которая позволяет измерить и «силу пункта» (трудность задания), и величину свойства (способность испытуемого) в одной шкале.
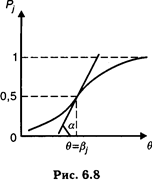
Эмпирически эта процедура производится следующим образом. Предполагается, что данные тестирования и значения латентных переменных характеризуются нормальным распределением. Уровень «способности» испытуемого в «логитах» определяется на шкале интервалов с помощью формулы:
где п — число испытуемых, рi — доля правильных ответов i -го испытуемого на задания теста, qi. — доля неправильных ответов,
Для первичного определения трудности задания в логитах используют оценку
pj + qj = 1. Хотя параметры b и q изменяются от «плюса» до «минуса», то при b < –6 значения рi близки к единице, т. е. на эти задания практически каждый испытуемый дает правильный («ключевой») ответ. При b < 6 с заданием не сможет справиться ни один испытуемый, точнее — вероятность дать «ключевой» ответ ничтожна. Рекомендуется рассматривать лишь интервалы от –3 до +3 как для b (трудности), так и для q (способность). Второй этап шкалирования испытуемых и заданий сводится к тому, что шкалы преобразуются в единую шкалу путем «уничтожения» влияния трудности задания на результат индивидов. И к тому же элиминируется влияние индивидуальных способностей на решение заданий различной трудности. Для шкалы испытуемых:
где
b — среднее значение логитов трудности заданий теста, W — стандартное отклонение распределения начальных значений параметра b, п — число испытуемых. Для шкалы заданий:
где
`q — среднее значение логитов уровней способностей, V— стандартное отклонение распределения начальных значений «способности», п — число заданий в тесте. Эти эмпирические оценки используются в качестве окончательных характеристик измеряемого свойства и самого измерительного инструмента (заданий теста). Если перед исследователем стоит задача конструирования теста, то он приступает к получению характеристических кривых заданий теста. Характеристические кривые могут накладываться одна на другую. В этом случае избыточные задания выбраковываются. На определенных участках оси q («способность») характеристические кривые заданий могут вовсе отсутствовать Тогда разработчик теста должен добавить задания недостающей трудности, чтобы равномерно заполнить ими весь интервал шкалы логитов от –6 до +6. Заданий средней трудности должно быть больше, чем на «краях» распределения, чтобы тест обладал необходимой дифференцирующей (различающей) силой. Вся процедура эмпирической проверки теста повторяется несколько раз, пока разработчик не останется доволен результатом работы. Естественно, чем больше заданий, различающихся по уровню трудности, предложил разработчик для первичного варианта теста, тем меньше итераций он будет проводить. Главным недостатком модели Раша теоретики считают пренебрежение «крутизной» характеристических кривых «крутизна» их полагается одинаковой. Задания с более «крутыми» характеристическими кривыми позволяют лучше «различать» испытуемых (особенно в среднем диапазоне шкалы способностей), чем задания с более «пологими» кривыми. Параметр, определяющий «крутизну» характеристических кривых заданий, называют дифференцирующей силой задания. Он используется в двухпараметрической модели Бирнбаума. Модель Бирнбаума аналитически описывается формулой
Параметр aj определяет «крутизну» кривой в точке ее перегиба; его значение прямо пропорционально тангенсу угла наклона касательной к характеристической кривой задания теста в точке Интервал изменения параметра aj от –¥ до +¥. Если значения a близки к 0 (для заданий разной трудности), то испытуемые, различающиеся по уровню выраженности свойства, равновероятно дают «ключевой» ответ на это задание теста. При выполнении такого задания у испытуемых не обнаруживается различий. Парадоксальный вариант получаем при a < 0. В этом случае более способные испытуемые отвечают правильно с меньшей вероятностью, а менее способные — с большей вероятностью. Опытные психодиагносты знают, что такие случаи встречаются в практике тестирования очень часто. Ф. М. Лорд и М. Новик в своей классической работе [Lord F. M., Novik M., 1968] приводят формулы оценки параметра a. При aj = 1 задание соответствует однопараметрической модели Раша. Практики рекомендуют использовать задания, характеризующие значение a в интервале от 0,5 до 3. Все психологические тесты можно разделить в зависимости от формального типа ответов испытуемого на «открытые» и «закрытые». В тестах с «открытым» ответом, к которым относятся тест WAIS Д. Векслера или методика дополнения предложений, испытуемый сам порождает ответ. Тесты с «закрытыми» заданиями содержат варианты ответов. Испытуемый может выбрать один или несколько вариантов из предлагаемого множества. В тестах способностей (тест Дж. Равена, GABT и др.) предусмотрено несколько вариантов неправильного решения и один правильный. Испытуемый может применить стратегию угадывания. Вероятность угадывания ответа:
где п — число вариантов. Результаты эмпирических исследований показали, что относительная частота решения «закрытых» заданий отклоняется от теоретически предсказанных вероятностей двухпараметрической модели Бирнбаума. Чем ниже уровень способностей испытуемого (низкие значения параметра q), тем чаще он прибегает к стратегии угадывания. Аналогично, чем труднее задание, тем больше вероятность того, что испытуемый будет пытаться угадать правильный ответ, а не решать задачу. Бирнбаум предложил трехпараметрическую модель, которая позволила бы учесть влияние угадывания на результат выполнения теста. Трехпараметрическая модель Бирнбаума выглядит так:
Соответственно оценка «силы» пункта (трудности задания) в логистической форме модели
Сj характеризует вероятность правильного ответа на задание j в том случае, если испытуемый угадывал ответ, а не решал задание, т.е. при q —> 0. Для заданий с пятью вариантами ответов Сj становится более пологой, так как 0 < С < 1, но при всех С = 0 кривая поднимается над осью q на величину Сj. Тем самым даже самый неспособный испытуемый не может показать нулевой результат. Дифференцирующая сила тестового задания при введении параметра Сj снижается. Из этого следует нетривиальный вывод: тесты с «закрытыми» заданиями (вынужденным выбором ответа) хуже дифференцируют испытуемых по уровням свойства, чем тесты с «открытыми» заданиями. Дата добавления: 2016-06-06 | Просмотры: 662 | Нарушение авторских прав |
 нельзя характеризовать по отнесенности к свойству, так как
нельзя характеризовать по отнесенности к свойству, так как  — множество свойств, качественно не определенных. Следовательно, каждый испытуемый характеризуется лишь структурой своих ответов.
— множество свойств, качественно не определенных. Следовательно, каждый испытуемый характеризуется лишь структурой своих ответов. является отображением множества на точку. Вектор значений Рij характеризует индивидуальную меру выраженности свойства (в вероятностной интерпретации — вероятность его наличия) у испытуемого. Соответственно определены все отображения F 1', F2' и F3' (и обратные им). Если испытуемые обладают / не обладают свойством, то их можно разбить на основании результата тестирования на классы, имеющие и не имеющие свойства. При интерпретации данных используется следующий алгоритм: фиксируются индикаторы, проявленные испытуемым, подсчитывается индивидуальный показатель наличия или отсутствия у него свойства и принимается решение о его принадлежности к одному из дихотомических классов — А и `А (обладающих и не обладающих свойством).
является отображением множества на точку. Вектор значений Рij характеризует индивидуальную меру выраженности свойства (в вероятностной интерпретации — вероятность его наличия) у испытуемого. Соответственно определены все отображения F 1', F2' и F3' (и обратные им). Если испытуемые обладают / не обладают свойством, то их можно разбить на основании результата тестирования на классы, имеющие и не имеющие свойства. При интерпретации данных используется следующий алгоритм: фиксируются индикаторы, проявленные испытуемым, подсчитывается индивидуальный показатель наличия или отсутствия у него свойства и принимается решение о его принадлежности к одному из дихотомических классов — А и `А (обладающих и не обладающих свойством).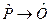 . Тем самым применяется следующая интерпретация: фиксируются ответы испытуемого; вычисляется «сырой» балл; испытуемый обладает определенной интенсивностью свойства на основе отображения «сырого» балла на шкалу, характеризующую свойство. Эта модель — модель латентного континуума — является наиболее распространенной при тестировании психических свойств.
. Тем самым применяется следующая интерпретация: фиксируются ответы испытуемого; вычисляется «сырой» балл; испытуемый обладает определенной интенсивностью свойства на основе отображения «сырого» балла на шкалу, характеризующую свойство. Эта модель — модель латентного континуума — является наиболее распространенной при тестировании психических свойств.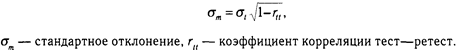
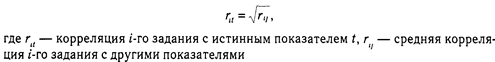
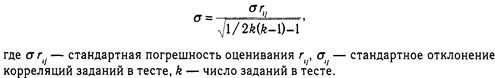
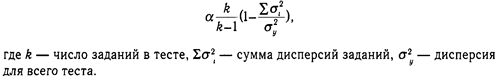
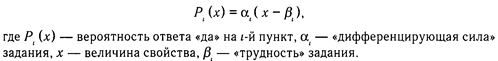
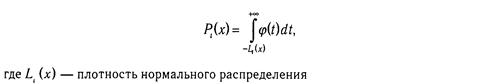
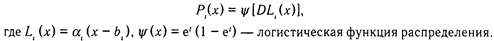
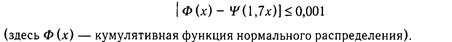
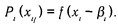
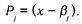
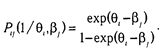
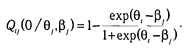
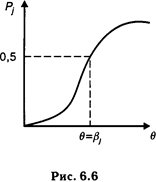
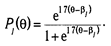
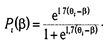
 является монотонно возрастающей.
является монотонно возрастающей.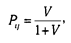
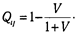
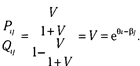
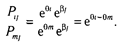
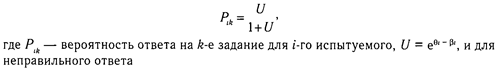
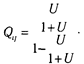
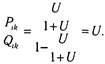
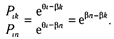
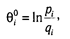
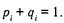
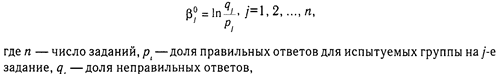
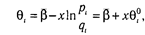
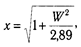
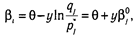
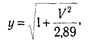
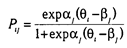
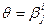 (рис 6.8).
(рис 6.8).