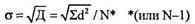АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Меры изменчивости (рассеивания, разброса)

Это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, о его компактности, а косвенно – и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: размах, среднее отклонение, дисперсия, стандартное отклонение, полуквартильное отклонение. Размах (Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.

Примеры: 0, 2, 3, 5, 8 (Р = 8-0 = 8);

-0.2, 1.0, 1.4, 2.0 (Р = 2,0-(-0,2) = 2,2);0,2,3,5,67 (Р = 67-0 = 67).

Среднее отклонение (МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним:

МД = ∑d / N,

где d = |Х– M|; М – среднее выборки; X – конкретное значение; N – число значений.

Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если их не взять по абсолютной величине, то их сумма будет равна нулю. И вся информация пропадает. МД показывает степень скученности данных вокруг среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции – моду или медиану.

Дисперсия (Д) (от лат. dispersus – рассыпанный). Другой путь измерения степени скученности данных – это избегание нулевой суммы конкретных разниц (d = Х-М) не через их абсолютные величины, а через их возведение в квадрат, и тогда получают дисперсию:

Д = ∑d² / N – для больших выборок (N > 30); Д = ∑d²/ (N-1) – для малых выборок (N < 30).

Стандартное отклонение (а). Из-за возведения в квадрат отдельных отклонений d при вычислении дисперсии получается очень не наглядная величина, далекая от самих отклонений. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим или стандартным отклонением:

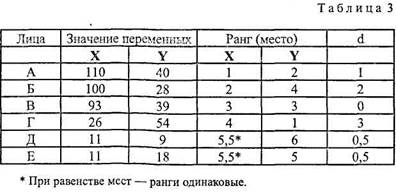
МД, Д и s применимы для интервальных и пропорциональных данных.

Для порядковых данных обычно в качестве меры изменчивости берут полуквартилыше отклонение (Q), именуемое еще полукваргттьным коэффициентом или полумеждуквартильным размахом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале (на графиках, полигонах, гистограммах отсчет обычно ведется слева направо), то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом Q₁. Вторые 25% распределения – второй квартиль, а соответствующая точка на шкале – Q₂. Между третьей и четвертой четвертями распределения расположена точка Q₃. Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:

Q = (Q₃ – Q₁)/2.

Понятно, что при симметричном распределении точка Q₂ совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. И тогда дополнительно вычисляют еще два коэффициента Q – для правого и левого участков:

Q_лев. = (Q₂-Q₁)/2; Q_прав. = (Q₃-Q₂)/2

Меры связи

Предыдущие показатели, именуемые статистиками, характеризуют совокупность данных по одному какому-либо признаку. Этот изменяющийся признак называют переменной величиной или просто «переменной». Меры связи же выявляют соотношения между двумя переменными или между двумя выборками.

Например, нужно установить, существует ли связь между ростом и весом человека, между типом темперамента и успешностью решения интеллектуальных задач и т. д. Или, скажем, надо выяснить, принадлежат ли две выборки к одной популяции или к разным. Эти связи, или корреляции (от лат. correlatio – соотношение, взаимосвязь), и выявляют через вычисление коэффициентов корреляции (R), если переменные находятся в линейной зависимости между собой. Считается, что большинство психических явлений подчинено именно линейным зависимостям, что и предопределило широкое использование методов корреляционного анализа. Но наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость [у = f(x)] – это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных причина, а какая – следствие. Кроме того, любая обнаруженная в психологии связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи психологических признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.

Виды корреляции: I. По тесноте связи:

1) Полная (совершенная) – R=l. Констатируется обязательная взаимозависимость между переменными. Здесь уже можно говорить о функциональной зависимости. Например: связь между стороной квадрата и его площадью, между весом и объемом и т. п.

2) Отсутствие связи – R = 0. Например: между скоростью реакции и цветом глаз, длиной ступни и объемом памяти.

3) Частичная – 0<R<l; (меньше 0,2) – очень слабая связь, трудно о ней говорить всерьез; (0,2–0,4) – корреляция явно есть, но невысокая; (0,4-0,6) – явно выраженная корреляция; (0,6-0,8) – высокая корреляция; (больше 0,8) – очень высокая.

Встречаются и другие градации оценок тесноты связи [288]. Кроме того, в психологии при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Эта классификация ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. Тогда чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей. А для малых выборок даже абсолютно большое значение R может оказаться недостоверным [344].

II. По направленности:

1) Положительная (прямая).

Коэффициент R со знаком «плюс» означает прямую зависимость: увеличение значения одной переменной влечет увеличение другой. Например, связь между числом повторений и запоминанием положительна.

2) Отрицательная (обратная).

Коэффициент R со знаком «минус» означает обратную зависимость: увеличение значения одной переменной влечет уменьшение другой. Например, увеличение объема информации ухудшает ее запоминание.

III. По форме:

1) Прямолинейная.

При такой связи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Например, последовательному изменению величины стороны прямоугольника соответствует столь же последовательное изменение его площади. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными.

В психологии строго прямолинейные связи – явление не частое. Например, иногда наблюдается прямолинейная связь между тренированностью и успешностью деятельности. 2) Криволинейная.

Это связь, при которой равномерное изменение одного признака сочетается с неравномерным изменением другого. Эта ситуация типична для психологии. Классическими иллюстрациями могут служить знаменитые законы Йеркса–Додсона и Вебера-Фехнера. Согласно первому успешность деятельности при увеличении мотивации к ней изменяется по колоколообраз-ной кривой: до определенного уровня рост мотивации сопровождается увеличением успешности, после чего с повышением мотивации успешность деятельности спадает. Согласно второму закону интенсивность наших ощущений при равномерном увеличении стимула увеличивается по логарифмической кривой, т. е. при изменении стимуляции в арифметической прогрессии ощущения изменяются в геометрической прогрессии.

Формулы коэффициента корреляции

1. При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (р):

p = 6Sd²/N(N²-l),

где d – разность рангов (порядковых мест) двух величин; N – число сравниваемых пар величин двух переменных (X и Y). Пример вычисления р дан в таблице 3.

2. При сравнении метрических данных используется коэффициент корреляции произведений по К.Пирсону (г):

r = Sxy/Nσ_xσ_y,

где х – отклонение отдельного значения X от среднего выборки (М_х); у – то же для Y; σ_х – стандартное отклонение для X; σ_у – то же для Y; N – число пар значений X и Y.

Рекомендации по анализу коэффициентов корреляции

1. R – это не процент соответствия переменных, а только степень связи.

2. Сравнение коэффициентов дает только неметрическуюинформацию, т. е. нельзя говорить, на сколько или во сколько раз один больше или меньше другого. Они сравниваютсяв оценках «равно – неравно», «больше – меньше». Можно сказать, что один коэффициент превышает (слабо, заметно, очень заметно) другой, но какова величина этого превышения говорить нельзя.

3. Существуют явления, в которых заведомо известно, чтомежду ними слабая (или сильная) связь. Тогда R приобретает не абсолютный, а относительный характер. Так, для слабой связи R = 0,2 может считаться высоким показателем, а для сильной и R = 0,7 будет считаться низким.

4. Иногда и слабая корреляция заслуживает внимания, еслиэто обнаружено впервые, т. е. выявлена новая связь.

5. Надежность R зависит от надежности исходных данных.

Дата добавления: 2016-06-06 | Просмотры: 750 | Нарушение авторских прав