АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

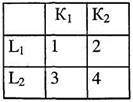
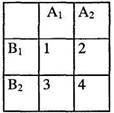
Требования к процедуре предъявления НП

Конкретное предъявление и изменение НП зависит от задач исследования и методической специфики. Но есть и некоторые общие требования.

Во-первых, желательно иметь одновременно влияние только одной НП. Такие опыты называют «чистым экспериментом» [120, с. 115]. Если экспериментатором выделено две или несколько НП, то необходимо все кроме одной в данном опыте исключить. Остальные предъявлять поочередно в других экспериментах, исключая предыдущие НП. Если такого порядка добиться невозможно или в случае интереса к совместному воздействию двух или нескольких НП, то прибегают к специально предусмотренному режиму предъявления стимуляции, разработка которого носит наименование «планирование эксперимента». Об этом планировании поговорим чуть позже.

Второе требование: необходимо исключить одновременное изменение с НП других существенных условий экспериментальной ситуации. Это достигается контролем за ДП. Если этого добиться не удается, то могут быть три варианта решения проблемы. Либо пересмотреть экспериментальную ситуацию с целью исключения соответствующей ДП, либо косвенно учесть вклад ее влияния на ответ (предельный случай – проигнорировать это влияние), либо принять ее еще за одну НП и предусмотреть при планировании эксперимента.

Третье требование: максимум точности при изменении НП. В экспериментах с количественными НП это требование выливается в требование возможности измерения переменной. Во многих случаях отсюда следует необходимость использования специальных средств экспонирования стимуляции. Переменные, не поддающиеся изменению экспериментатором, изменяются через тщательный подбор испытуемых. Сюда относятся такие параметры как пол, возраст, способности, ЗУН и т. п.

Планирование эксперимента

Планирование эксперимента входит составной частью в общее планирование исследования, представляющее один из этапов исследовательского процесса, предшествующий непосредственному проведению опытов. «Планирование эксперимента – это раздел знаний, относящийся не только и не столько к математической статистике, сколько к логике» [231, с. 122]. Суть его заключается в составлении набора экспериментальных ситуаций с определенными комбинациями независимых и зависимых переменных [18, 48, 211, 388, 395].

Иногда планирование эксперимента толкуется расширительно: как обеспечение валидности опыта [120,356]. В самом общем плане под валидностью понимается соответствие метода задаче исследования. Для обеспечения валидности эксперимента тогда необходимо составить перечень всех видов переменных и продумать не только план предъявления независимых переменных, но и предусмотреть процедуры контроля дополнительных переменных. Эти ДП обычно рассматриваются как факторы, «угрожающие» валидности [178].

Мы в своем изложении будем придерживаться более традиционного узкого толкования планирования эксперимента – как части планирования эмпирической процедуры, касающейся лишь порядка предъявления НП. Тогда в зависимости от количества независимых и зависимых переменных возможны четыре типа планов:

1) Одна НП и одна ЗП. Этот тип называют одновариантным, или однофакторным планом. Наиболее часто встречающийся в исследовательской практике вариант. Можно сказать,что это «классический» вариант эксперимента. Посколькуизмерению и контролю подлежат только две переменные,этот тип эксперимента часто называют двумерным, или бивалентным.

2) Одна НП и несколько ЗП. В экспериментальной практикевариант встречается редко.

3) Несколько НП и одна ЗП. Распространенный вариант.Именно он обычно противопоставляется первому типу, когда говорят о многовариантном, многомерном, многофакторном или многоуровневом планировании и экспериментировании.

4) Несколько НП и несколько ЗП. Вариант так же редок, каки второй тип.

В дальнейшем изложении будем иметь в виду первый и третий типы эксперимента как наиболее характерные для психологических исследований. О планировании эксперимента как о предусмотрении необходимых ситуаций воздействия на испытуемого в полной мере обычно говорят лишь при многомерном эксперименте. В случае «классическом» нет особой нужды в специальном планировании, поскольку нет комбинаций воздействующих факторов – всего одна НП, имеющая некоторое заданное экспериментатором число значений. Эта процедура характерна для экспериментирования на функциональном уровне.

В многомерном эксперименте совокупность комбинаций переменных должна охватить все основные варианты возможного влияния НП на ЗП. И тогда для исчерпывающего ответа на вопросы, что и как влияет на реакции испытуемого, и для рационального расходования времени и ресурсов прибегают к специальному планированию и составлению необходимых сочетаний отдельных значений различных переменных. Эти значения могут относиться к переменным, выражаемым как количественно, так и качественно. Сочетаемые значения переменных П. Фресс именует «степенями переменных» [388, с. 135], К. У. Эттрих– «ступенями» и «модальностями» переменных [424, с. 471], Дж. Стенли и Дж. Гласе – «уровнями факторов» [87, с. 438], Р. -Готтсданкер – «условиями или уровнями переменной» [92, с. 363].

Подобное планирование осуществляется преимущественно при экспериментировании на факторном уровне. Составляемые планы позволяют выяснить, оказывает ли НП заметное влияние на ЗП. Но они не позволяют выяснить функциональной связи между НП и ЗП. Это удается сделать только в эксперименте с одной НП, изменения которой имеют количественный характер.

Идея планирования эксперимента обычно связывается с именем Р. Фишера, разрабатывавшего в этих целях метод дисперсионного анализа. Первые внедрения этого планирования относятся к агробиологии. В психологию планирование эксперимента введено около 1940 г.

Указанное планирование может осуществляться различными способами: факторное планирование; методы латинского и греко-латинского квадратов; методы латинского прямоугольника и куба; вариации латинского квадрата в виде диагональных, сбалансированных и частично сбалансированных неполноблочных планов; дробные факторные планы. Рассмотрим лишь три первых метода как базовые способы планирования.

а. Факторное планирование предусматривает все возможные сочетания значений независимых переменных. Проиллюстрируем этот метод примерами. Для наглядности представим их в табличной форме.

Допустим, имеются две НП с двумя значениями каждая: К₁, К₂ и L₁, L₂. Тогда возможны 4 их сочетания, т. е. 4 экспериментальных ситуации (2x2): 1) К₁, L₁; 2) К₂ L₁; 3) К₁, L₂; 4) К₂ L₂:

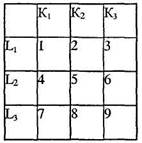
Для двух переменных с тремя значениями каждая будет иметь 9 ситуаций (3x3): 1) К₁L₁; 2) К₁L₂; 3) К₁L₃; 4) К₂L₁; 5) К₂L₂; 6) К₂L₃; 7) К₃L₁; 8) К₃L₂; 9) K₃L₃:

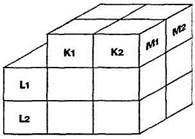
Для трех переменных с двумя значениями каждой имеем 8 ситуаций (2x2x2): 1) К₁,L₁,М₁; 2) К₁,L₁,М₂; 3) К₁,L₂,М₁; 4) К₁,L₂,М₂; 5) К₂,L₁,М₁; 6) К₂,L₁,М₂; 7) К₂,L₂,М₁; 8) К₂,L₂,М₂:

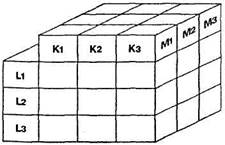
Для трех переменных с тремя значениями будет 27 сочетаний (3x3x3):

Таким образом, общее число возможных сочетаний определяется произведением показателей числа значений по каждому фактору (переменной). Для двух факторов с числом значений «К» для первого и «L» для второго число сочетаний равно KxL. Для трех факторов с числом значений соответственно К, L, М число сочетаний равно KxLxM. Для 4 факторов с показателями К, L, М, N число сочетаний равно KxLxMxN. И так далее.

В чем достоинство факторного планирования по сравнению с процедурой, предусматривающей изменение только одной переменной? Рассмотрим этот вопрос на простом примере, приводимом П. Фрессом в его «Экспериментальном методе» [388, с. 137–138]. Изучается влияние ожидания на время реакции (ВР) при двух различных длительностях ожидания (А₁ = 20 с и А₂ = 60 с) и при двух типах ожидания (В₁= безразличное ожидание и В₂ = ожидание со страхом, когда сигнал сопровождается ударом электрического тока). Графически план выглядит так:

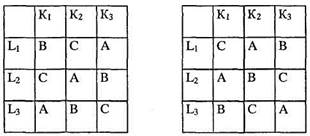
Тогда имеем: 1) измерения способствуют решению двух проблем одновременно: влияние длительности ожидания (влияние переменной А) и влияние характера ожидания (влияние переменной В). В эксперименте с изменением только одной переменной потребовалось бы для решения обеих этих проблем не четыре опыта (A₁B₁, A₂B₂, А,В₂, А₂В₂), а восемь: А А₁ и A₂ при условии В₁ а затем при В₂, после чего В₁ и В₂ в случае А₁ а потом в случае А₂; 2) расширяется база для анализа и индуктивных выводов, так как возможны разнообразные перегруппировки данных. Так, можно проверить влияние каждого фактора (каждого значения НП) по отдельности и сравнить его с общим влиянием данной переменной. Для A₁ — это ситуации 1 и 3, для A₂ — 2 и 4, для В₁ — 1 и 2, для В₂ — 3 и 4.

Очевидно, что в этом случае представляется возможность определить влияние взаимодействия переменных, чего в однофакторном эксперименте получить нельзя. Взаимодействие состоит в том, что влияние одной НП на зависимую переменную зависит от значения другой НП. В примере П. Фресса это означает, что влияние характера ожидания зависит от длительности. Скажем, ожидание со страхом по сравнению с нейтральным ожиданием по-разному влияет на время реакции в зависимости от того, короче оно или длиннее. Чтобы удостовериться в этом, нужно сравнить различия между ситуациями 1 и 2 с различиями между ситуациями 3 и 4. Если сравниваемые различия одного порядка – то взаимодействия нет, если же разного порядка– то взаимодействие НП налицо.

Факторное планирование удобно при небольшом числе переменных с небольшим числом их значений. Но даже незначительное увеличение числа НП или числа их значений резко увеличивает количество необходимых экспериментальных ситуаций.; Обилия ситуаций избегают путем искусственного ограничения количества сочетаний всех имеющихся значений переменных. Реализуется этот прием методами латинского и греко-латинского квадратов. Иногда эти методы называют «редуцированными г многовариантными планами» [424, с. 490-491].

б. Метод латинского квадрата. Этот прием используется при трех независимых переменных с несколькими значениями каждой из них. Принцип метода – каждая пара значений реализуется только один раз.

Практически строится таблица, где колонки соответствуют одной переменной, строки – второй, а каждая колонка и строка включали бы все значения третьей НП.

При трех переменных с тремя значениями каждой экспериментальный план выглядит следующим образом:

План включает 9 полей (ситуаций), тогда как при тех же условиях факторный план состоял бы из 27 ситуаций, а однофактор-ный (с одПлан включает 9 полей (ситуаций), тогда как при тех же условиях факторный план состоял бы из 27 ситуаций, а однофактор-ный (с одной НП) - из 81. Название метод получил по сложив-ной НП) - из 81. Название метод получил по сложившейся традиции обозначать показатели третьей переменной, а соответственно и получающиеся ситуации буквами латинского алфавита (А, В, С). Видно, что строки и колонки квадрата однородны: каждая есть совокупность ситуаций А, В и С. Это позволяет трижды перегруппировать результаты (по строкам, колонкам и буквам), что дает возможность проверить влияние каждой переменной по отдельности. Выявить взаимодействие переменных здесь весьма сложно. Но можно нейтрализовать влияние этого взаимодействия, увеличивая число разновидностей планов, изменив в строках и колонках порядок букв:

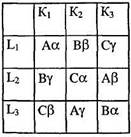
Полный набор вариантов тогда по сути повторяет комбинацию сочетаний по факторному плану. Что лучше? Выбирает экспериментатор.

в. Метод греко-латинского квадрата позволяет ввести четвертую переменную. К каждой латинской букве плана добавляется греческая буква, соответствующая значениям четвертой переменной. Распределение греческих букв подчиняется тому же закону, что и латинских: оно должно быть полным в каждой строке и колонке и таким, чтобы 3-я переменная (латинская буква) появлялась в каждом случае только один раз при появлении 4-й НП (греческой буквы). При трех значениях каждой из четырех НП план выглядит следующим образом:

Полученный план включает 9 ситуаций. Аналогичный вариант по факторному плану состоял бы из 3x3x3x3=81 ситуации.

Существуют, как уже говорилось, и другие, более сложные планы, нежели рассмотренные нами три метода. Но все они зиждятся на том же принципе: перегруппировка частных данных и их сравнение с совокупностями других результатов. Напомним, что любой экспериментальный план, во-первых, эффективен лишь на факторном уровне эксперимента и, во-вторых, может трансформироваться в другие виды при так называемом гибком планировании. Суть последнего – в одновременном исполнении исследовательских этапов планирования, сбора эмпирических данных и их обработки. Подобное совмещение разных по сути исследовательских процедур возможно при компьютерном варианте экспериментирования, когда «исследователь имеет возможность оценивать целостную картину полученных результатов после каждого промежуточного этапа проведения эксперимента (в полностью автоматизированном эксперименте минимальный шаг может равняться отдельной пробе)» [153, с. 48].

В целом, не принижая важности планирования эксперимента, не следует слишком переоценивать его значение в психологических исследованиях. Причина проста. Количество переменных в психологических опытах бесконечно. Учесть даже малую их толику невозможно. Поэтому исследователь выбирает, опираясь на свои опыт и интуицию, минимум переменных, наиболее существенных, по его мнению. Увеличение числа переменных и, как следствие, загромождение экспериментального исследования сложнейшими планами, которые в реальных условиях зачастую не выполнить, ведет к потере нити исследования и побледнению психологической специфики на фоне логико-математических манипуляций. «Деревья заслоняют лес». А уровень точности и тонкости исследования предопределяется не столько тщательностью планирования порядка предъявления НП и контроля ДП, сколько первичным отсевом действующих в реальности переменных.

Никоим образом не умаляя ценности самых широких и изощренных разработок в области планирования эксперимента и внедрения разнообразных планов в психологические исследования, все же следует предостеречь от гипертрофированного увлечения этой процедурой и придания ей статуса «центрального звена» [120, с. 93] всего процесса психологического экспериментирования.

Подробнее и в более широком контексте, ориентированном на перспективы развития психологических исследований, с вопросом планирования эксперимента можно познакомиться в целом ряде работ [3, 120, 165, 178 и др.].

Дата добавления: 2016-06-06 | Просмотры: 673 | Нарушение авторских прав