АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Пример задачи с ненулевым значением дополнительной двойственной переменной

Изменим условия рассмотренного примера. Пусть теперь карамель «Снежинка» приносит 230 руб. прибыли на тонну. Отчет по устойчивости, который будет при этом получен, примет вид таблицы 36.

Итак, при таких исходных данных фабрике следует выпускать только 1000 т карамели «Снежинка». Оптимальная прибыль при этом составит 230000 руб.

Из таблицы 34 видно, что у₅ = 3,75. Это означает, что если будет необходимо выпустить хотя бы одну тонну карамели «Яблочная», прибыль фабрики сократится на 3,75 руб.

Таблица 36 – Отчет по устойчивости для переменных

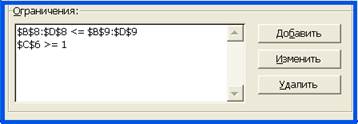
Чтобы убедиться в этом, добавим в «Поиск решения» еще одно ограничение, как показано на рисунке 40. Здесь новое ограничение $C$6>=1 означает, что х₂ ³ 1, т.е. выпуск карамели «Яблочная» должен составить не менее тонны.

Рисунок 40 – Новая система ограничений

После выполнения «Поиска» диапазон ячеек электронной таблицы А4:D11 примет вид таблицы 37, из которой видно, что в этих условиях оптимальная прибыль составит 229996,25 руб.

Она уменьшилась по сравнению с 230000 руб., т.к. чтобы выпустить 1 т карамели «Яблочная», пришлось выделить часть ресурсов. В результате сократился выпуск «Снежинки», и можно произвести не 1000 т этой карамели, а всего 999,375 руб.

Таблица 37 – Результаты «Поиска решения»

Чтобы определить, на сколько сократилась прибыль, введем в ячейку В12 формулу =230000-B11. Результат также представлен в таблице 37 и составляет 3,75 руб., т.е. у₅.

Вопросы и упражнения

1 Как обратиться к «Поиску решения»?

2 Опишите диалоговое окно «Поиска решения».

3 Как ввести ограничения задачи для «Поиска решения»?

4 Какие параметры «Поиска решения» Вы знаете?

5 Как пользоваться кнопками «Сохранить модель» и «Загрузить модель»?

6 Опишите диалоговое окно «Результаты поиска решения».

7 Какие итоговые сообщения могут быть выведены «Поиском» для линейной задачи?

8 Какие отчеты можно получить с помощью «Поиска решения»?

9 Опишите содержание «Отчета по результатам».

10 Опишите содержание «Отчета по устойчивости».

11 Опишите содержание «Отчета по пределам».

12 Задачу 9 из раздела 1.5 поставьте для «Поиска решения».

13 Получите все типы отчетов для этой задачи и проанализируйте их.

14 Сохраните построенную модель.

15 Задачи из раздела 4.2 поставить для «Поиска решения» и для разрешимой задачи проанализировать все типы отчетов.

* Здесь принципиально важно, чтобы формулы не копировались, а именно переносились, т.к. в случае копирования ссылки в формулах изменятся.

* Для целочисленных задач это сообщение иногда выдается ошибочно, что связано с недостатками программного обеспечения.

* Таким образом, если модель не линейная, то отчет по устойчивости будет иметь иную форму, нежели описано в этом разделе. В случае если Вы получили такой отчет, следует проверить, установлен ли в «Параметрах» «Поиска» флажок «Линейная модель».

* Запись «1Е+30» означает 10³⁰. В данном контексте это означает бесконечность.

* Если «Поиск решения» не выдает другой оптимальный план, можно уменьшить коэффициент 224 на очень малое в рамках модели число (например, взять коэффициент 223,999). В этом случае «Поиск решения» выдает оптимальный план (266,7; 1173,3) и оптимум 223999,73. Изменив содержимое ячейки В4 снова на 224, легко убедиться, что целевая функция примет значение 224000, равное оптимуму, т.е. этот план – тоже оптимальный.

* Здесь же отметим, что оптимальный план прямой задачи – не вырожденный, так как есть три ненулевые переменные – х₁, х₄ и х₅. А вот оптимальный план двойственной задачи – вырожденный, так как ненулевая переменная всего одна – у₁ = 280.

Дата добавления: 2015-01-18 | Просмотры: 471 | Нарушение авторских прав