АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

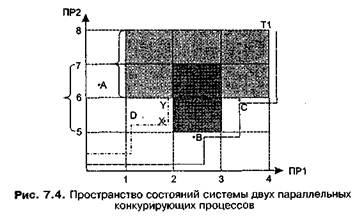
Пример тупика на ресурсах типа SR

Предположим, что существуют два процесса ПР1 и ПР2, разделяющих два ре­сурса типа SR: Ri и R2. Пусть взаимное исключение доступов к этим ресурсам реализуется с помощью семафоров S1 и S2 соответственно. Процессы ПР1 и ПР2 обращаются к ресурсам следующим образом [37] (рис. 7.3):

Процесс ПР1 Процесс ПР2

1: P(S2); 5: P(S1);

2: P(S1); 6: Р (S2);

3: V(S1); 7: V(S1); ^ч

4: V(S2); 8: V(S2);

Рис. 7.З. Пример последовательности операторов для двух процессов, которые могут привести к тупиковой ситуации

Здесь несущественные (с точки зрения обращения к ресурсам) детали опущены. Считаем, что оба семафора первоначально установлены в единицу. Пространст­во возможных вычислений приведено на рис. 7.4.

Горизонтальная ось задает выполнение процесса ПР1, вертикальная — ПР2. Вер­тикальные линии, пронумерованные от 1 до 4, соответствуют операторам 1-4 процесса ПР1. Аналогично горизонтальные линии, пронумерованные от 5 до 8, соответствуют операторам 5-8 программы ПР2. Точка на плоскости определяет состояние вычислений в некоторый момент времени. Так, точка А соответствует ситуации, при которой ПР1 начал исполнение, но не достиг оператора 1, а ПР2 выполнил оператор 6, но не дошел до оператора 7. По мере выполнения точка будет двигаться горизонтально вправо, если исполняется ПР1, и вертикально вверх, если исполняется ПР2.

Интервалы исполнения, во время которых ресурсы R1 и R2 используются каждым процессом, показаны с помощью фигурных скобок. Линии 1-8 делят простран­ство вычислений на 25 прямоугольников, каждый из которых задает состояние вычислений. Закрашенные серым цветом состояния являются недостижимыми из-за взаимного исключения ПР1 и ПР2 при доступе к ресурсам R1 и R2.

Рассмотрим последовательность исполнения 1-2-5-3-6-4-7-8, представленную траекторией Т1. Когда процесс ПР2 запрашивает ресурс R1 (оператор 5), ресурс недоступен (оператор выполнен, семафор закрыт). Поэтому процесс ПР2 забло­кирован в точке В. Как только процесс ПР1 достигнет оператора 3, процесс ПР2 деблокируется по ресурсу R1. Аналогично в точке С процесс ПР2 будет заблоки­рован при попытке доступа к ресурсу R2 (оператор 6). Как только процесс ПР1 достигнет оператора 4, процесс ПР2 деблокируется по ресурсу R2.

Если же, например, выполняется последовательность 1-5-2-6, то процесс ПР1 заблокируется в точке X при выполнении оператора 2, а процесс ПР2 заблокиру-ется в точке Y при выполнении оператора 6. При этом процесс ПР1 ждет, когда процесс ПР2 выполнит оператор 7, а ПР2 ждет, когда ПР1 выполнит оператор 4. Оба процесса будут находиться в тупике, ни ПР1, ни ПР2 не могут закончить выполнение. При этом все ресурсы, которые получили ПР1 и ПР2, становятся недоступными для других процессов, что резко снижает возможности вычисли­тельной системы по обслуживанию их. Отметим одно очень важное обстоятель­ство: тупик будет неизбежным, если вычисления зашли в прямоугольник D, яв­ляющийся критическим состоянием.

Для того чтобы возник тупик, необходимо, чтобы одновременно выполнялись четыре условия [37, 92]:

О взаимного исключения, при котором процессы осуществляют монопольный доступ к ресурсам;

Q ожидания, при котором процесс, запросивший ресурс, ждет до тех пор, пока запрос не будет удовлетворен, при этом удерживая ранее полученные ресурсы;

Q отсутствия перераспределения, при котором ресурсы нельзя отобрать у про­цесса, если они ему уже выделены;

О кругового ожидания, при котором существует замкнутая цепь процессов, каж­дый из которых ждет ресурс, удерживаемый его предшественником в этой цепи.

Проанализировав содержательный смысл этих четырех условий, легко убедить­ся, что все они выполняются в точке Y (см. рис. 7.4).

Дата добавления: 2015-01-18 | Просмотры: 593 | Нарушение авторских прав