 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Способы нормирования исходных данных
Обозначения:
Ясно, что распространенные способы нормирования применимы лишь к данным, полученным в шкалах интервалов и отношений. Применение этих способов к номинальным или порядковым данным является некорректным. Для таких шкал нормирование обычно не проводится, однако в качестве «компенсации» выбираются соответствующие адекватные меры различия или сходства, рассматриваемые ниже. Кроме того, заметим, что приведенные в табл. 11.2-2 способы нормирования выполняются «по столбцу», однако, при необходимости аналогичное нормирование можно выполнить «по строке». Более подробную информацию о проблеме нормирования показателей при построении матрицы «объект-признак» можно получить в [4. C.27-28], где имеются ссылки на дополнительные источники. Далее необходимо представить данные в виде точек многомерного пространства, снабженных соответствующим набором координат. Для этого, в первую очередь, исследователю надо принять решение о направлении кластеризации, то есть о том, что именно будет подвергаться разделению на кластеры: объекты (случаи), признаки (измеряемые переменные), или и то, и другое одновременно. В психологических исследованиях часто встречается и кластеризация объектов, и кластеризация признаков; третий вариант (одновременная кластеризация и объектов, и признаков) используется сравнительно редко и не будет рассматриваться в пособии; прочитать о нем можно в работе автора этого подхода Дж.А.Хартигана (G.A.Hartigan) [41]. После принятия решения о направлении кластеризации исследователь получает возможность представить эмпирические данные в виде элементов (точек) некоторого многомерного пространства. В соответствии с альтернативой решения о направлении кластеризации (объекты или признаки) возможное представление выборки также двойственно, так как ее можно представить следующими способами: · Как набор из n точек · Как набор из m точек Вопрос о том, как именно представлять эмпирические данные, решает исследователь, исходя из поставленной цели. В зависимости от его решения образуемое для представления данных метрическое пространство будет иметь размерность: равную либо n - числу объектов, либо m - числу подвергаемых измерению признаков каждого объекта. Никаких принципиальных различий в самой процедуре для вариантов кластеризации объектов или признаков нет: для кластерного анализа, в определенном смысле, «все равно» что именно подвергать классификации: объекты (респондентов) или признаки (свойства). При последующем обсуждении для определенности будем считать, что исследователя интересует кластеризация объектов (случаев). Полученное таким образом многомерное пространство эмпирических данных для осуществления возможности кластеризации необходимо превратить в метрическое: построение метрического пространства предполагает не только задание координат точек, но и выбор расстояния между ними (метрики). Таким образом, понятие метрического пространства неразрывно связано с понятиями пространства и метрики. Рассмотрим эти понятия. В математике известно, что понятие пространства, как и понятие множества, являются наиболее базовыми, фундаментальными, и поэтому не имеют точного и математически строгого определения; считается, что эти понятия доступны нам на интуитивном уровне. С учетом этого обстоятельства, пояснить (а не определить) понятия множества и пространства можно следующим образом: под множеством понимается совокупность (конечная или бесконечная) некоторых объектов произвольной природы (людей, точек, чисел и т.д.). В свою очередь, пространство – это некоторое множество объектов, для которой заданы какие-либо структурные свойства (например, взаимная упорядоченность объектов или другие взаимосвязи между ними). Приняв понятия множества и пространства на интуитивном уровне, мы можем уже более строго дать следующее определение: метрическим пространство пространства (в нашем случае задана функция расстояния следующим условиям для любых элементов Неотрицательность: Рефлексивность: Симметричность: Транзитивность: Нередко при применении кластерного анализа, особенно в области психологии, эти требования к расстоянию ослабляют, отказываясь от некоторых из них: чаще всего - от транзитивности («неравенства треугольника»), или симметричности. В этом случае мы имеем дело уже не с «настоящей» метрикой, а с «ослабленной» (так как для нее выполняются не все фигурирующие в определении требования). Такие меры различия получили название псевдометрик, а конструируемое с их помощью пространство, соответственно, называется псевдометрическим. Подробное рассмотрение их особенностей выходит за рамки данной работы, поэтому в дальнейшем изложении, говоря о мерах различия, мы не будем различать метрики и псевдометрики, а также метрический или псевдометрический статус пространства. Дополнительную информацию об особенностях использовании псевдометрик в кластерном анализе можно получить в источниках [9; 22; 23; 28; 34; 35; 39]. Выбрав меру различия, исследователь получает возможность перейти от матрицы «объект-признак»
Матрица попарных расстояний имеет следующие особенности: · она – квадратная (то есть число строк в ней равно числу столбцов) и имеет; в рассматриваемом случае, размеры · любой элемент · она симметричная, так как по свойству симметричности расстояния 11.2-4 · на ее главной диагонали стоят нули, так как по свойству рефлексивности расстояния 11.2-3 Получив матрицу расстояний, можно перейти к последующим этапам процедуры кластеризации. Но во многих статистических пакетах вместо матрицы «объект-признак» можно изначально использовать в качестве входных данных процедуры кластеризации предварительно построенную матрицу расстояний. В предыдущем изложении мы опирались на понятие меры различия (расстояния, метрики), однако, возможен альтернативный подход к постановке задачи кластеризации, основанный на мере сходства (близости, похожести, подобия, толерантности) элементов метрического пространства. В математическом плане эти подходы эквивалентны, то есть приводят к одинаковым результатам кластеризации. Конкретный выбор одного из этих двух подходов часто определяется содержательным смыслом исследуемых явлений. При одной и той же глобальной стратегии кластеризации могут использоваться различные меры различия или сходства. Отдельные примеры мер различия и сходства приведены в табл. 11.2-3. Таблица 11.2-3 Примеры мер различия и сходства, используемых
Обозначения:
m - количество измеряемых признаков; r - степенной параметр метрики Минковского;
Каждая из мер, представленных в табл. 11.2-3, имеет свое назначение, область и особенности применения: · Евклидово расстояние является в кластерном анализе наиболее популярной метрикой; для трехмерного пространства оно совпадает с обычным «обыденным» расстоянием. Хотя евклидова метрика ориентирована, в первую очередь, на применение к данным, измеренным в шкалах интервалов или отношений, но на практике она часто применяется (хотя и не всегда корректно) и для данных, полученных в других шкалах. Евклидову метрику целесообразно применять для переменных, измеренных в одних и тех же единицах (или для нормированных данных); в противном случае целесообразно использовать нормированный вариант евклидовой метрики [3. С.212]. Обсуждение проблем применения евклидовой метрики имеется, например, в работах [5. С.157; 21. С.66]. · Расстояние «Манхетен» часто применяется для номинальных и дихотомических признаков [3. С.212]. Это расстояние равно сумме покоординатных различий между точками (иногда эту сумму делят на число координат, и тогда получается среднее покоординатное различие). Это расстояние во многом аналогично евклидовой метрике, однако при его применении сглаживается эффект больших различий по отдельным координатам (так как эти различия, в отличие от метрики Евклида, не возводятся в квадрат). Обсуждение данной метрики имеется в [5. С.158; 17. С.577; 19. С.87]. · Метрика Минковского; включает определяемый исследователем параметр r является обобщением случаев евклидова расстояния (r =2), метрики Манхетен (r =1) и некоторых других метрик. В силу этого данную метрику удобно использовать при экспериментах с расстоянием, гибко варьируя ее параметр. Обсуждение метрики Минковского имеется, например, в [5. С.158; 17. С.576]. · Коэффициент сходства Гауэра предназначен для решения задач, в которых одновременно используются признаки, измеренные в различных шкалах: интервальных, порядковых и дихотомических. В этом - его несомненное преимущество, тем более, что мер сходства для работы со смешанными шкалами относительно немного. К сожалению, коэффициент Гауэра редко используется в психологических исследованиях и не реализован в рассматриваемых статистических пакетах, поэтому методика его вычисления будет подробно рассмотрена нами при решении задачи 11.5-4. Обсуждение этого коэффициента имеется в [5. С.160-164; 17. С.290-294]. Кроме представленных в табл. 11.2-3, в кластерном анализе применяется множество иных мер сходства или различия: · Для интервальных данных - расстояния Squared Euclidean (Квадрат евклидова), Chebychev (Чебышева), Mahalanobis (Махаланобиса); мера близости Pearson correlation (Коэффициент корреляции Пирсона) и другие. На практике многие из этих мер применяются, хотя и далеко не всегда обоснованно, к данным, измеренным в неинтервальных шкалах. · Для порядковых данных - Chi-square measure (Мера хи-квадрат), Phi-square measure (Мера фи-квадрат), меры близости – коэффициенты ранговой корреляции Spearman (Спирмена), Kendall (Кендалла), Чупрова и другие. · Для номинальных и двоичных (дихотомических) данных - Variance (Рассеяние), Dispersion (Дисперсия); коэффициенты Hamming (Хемминга), Phi 4-point correlation (Четырехпольный коэффициент корреляции фи), Lambda (Ламбда), Anderberg’s D (D Андерберга), Jaccard (Джаккарда), Kulczynski (Кульчицкого), Lance and Williams (Ланса и Уильямса), Ochiai (Очиаи), Rogers and Tanimoto (Роджерса и Танимото), Russel and Rao (Русселя и Рао), Sokal and Sneath (Сокала и Снита), Yule’s Y (Коэффициент Юла Y), Yule’s Q (Коэффициент Юла Q) и другие. · Для данных, измеренных в смешанных шкалах, применяются меры близости Журавлева, Воронина, Миркина и другие. Итак, выбор конкретной меры различия или сходства определяется не только (и не столько) субъективным предпочтением исследователя, сколько объективными свойствами исследуемого явления, в частности, характером используемых измерительных шкал. Подробнее вопрос о мерах различия и сходства при кластерном анализе рассмотрен в работах [2; 3-5; 9; 17; 22; 23; 26; 35]. 11.3. Классификация методов кластерного анализа После того, как построено метрическое пространство, последующая часть процедуры кластерного анализа достаточно автономна: здесь уже неважно, как именно задавалась метрика и что именно (объекты или признаки) представлялось в виде точек пространства; главное, что к этому этапу построена матрица попарных расстояний (или попарных мер сходства) между представленными в виде точек многомерного пространства эмпирическими данными, с которой предстоит работать на последующих этапах кластерного анализа. Однако здесь исследователю предстоит решить не менее принципиальный вопрос о выборе глобальной стратегии кластеризации, то есть основного принципа ее осуществления. Вопрос о классификации методов кластерного анализа является весьма непростым: различные классификации предложены А.А.Дорофеюком, С.А.Айвазяном и др., Н.Г.Загоруйко, Б.Г.Миркиным, Дж.Гудом (I.J.Good), Р.Кормаком (R.M.Cormak), Дж.Хартиганом (J.A.Hartigan) (ссылки на источники имеются в [4. С.39]) и другими авторами. Так, Болл (G.H.Ball) разделяет все методы поиска кластеров на семь классов (цит. по [2. С.101]), а И.Д.Мандель приводит подробную «фасетную» классификацию [4. С.36-166]. Тем не менее, учитывая ориентированность нашего пособия на практическое применение статистических методов в психологии, приведем классификацию методов кластерного анализа (взяв за основу классификацию, предложенную И.Гайдышевым [17. C.363]), пусть несколько упрощенную и не вполне исчерпывающую, но достаточную для того, чтобы сориентировать читателя в необъятном море разработанных на сегодняшний день методов и алгоритмов кластеризации. Итак, по глобальным стратегиям кластеризации могут быть выделены следующие наиболее часто применяемые в психологических исследованиях классы методов: · иерархические методы, · итеративные методы группировки, · методы, использующие алгоритмы типа разрезания графа. В рамках пособия при решении задач мы будем применять только методы из первых двух классов (иерархические и итеративные), и поэтому сосредоточим на них основное внимание при дальнейшем изложении теоретического материала. Однако в психологических исследованиях иногда применяются и специфические методы третьего класса: метод корреляционных плеяд, разработанный русским гидробиологом П.В.Терентьевым; «вроцлавская таксономия» и др. Подробнее с подобными методами можно ознакомиться в [4; 9. С.415-417; 17. C.381-386]. В иерархических методах выстраивается «дерево» кластеров, то есть для полученных окончательных кластеров можно проследить «историю» их постепенного формирования путем объединения или разъединения первоначально существовавших кластеров (например, отдельных точек метрического пространства данных). В итеративных методах разбиение на кластеры получается из некоторого начального разбиения способом последовательных перерасчетов (приближений, итераций). Как иерархические, так и итеративные методы кластеризации, в свою очередь, часто подразделяют на дивизивные (разделительные) и агломеративные (объединительные). Для исследователя-психолога именно это деление является, по-видимому, основным, так как отражает желаемый результат применения кластерного анализа, а не его технологию (итеративное или «прямое» построение кластеров). В дивизивных иерархических методах множество исходных данных первоначально представляется как один кластер, который затем разделяется на некоторое (часто заранее заданное) количество кластеров. Процесс кластеризации заканчивается, когда получено разделение исходного множества данных на заданное число кластеров при определенном удовлетворяющем исследователя качестве разделения. На практике среди дивизивных чаще применяют не иерархические, а итеративные методы. В дивизивных итеративных методах также ведется разделение исходной совокупности точек на кластеры, но при этом иногда заранее выделяют некоторое количество так называемых «эталонных» кластеров, к которым постепенно присоединяются все оставшиеся эмпирические точки пространства данных. Процесс кластеризации также заканчивается, когда получено удовлетворительное качество разбиения. Популярным примером подобных методов является метод k -средних, который будет рассмотрен нами подробнее при решении соответствующих задач. При этом необходимо отметить, что вопрос о выборе критериев качества разбиения на кластеры является весьма сложным, объемным и рассматривается во многих работах: см., например, [2; 4; 5; 9]. Среди агломеративных методов, напротив, на практике чаще используют не итеративные, а иерархические (хотя существует множество и тех, и других). В агломеративных иерархических методах, каждый элемент (результат измерения) эмпирической выборки первоначально представляется отдельным кластером. Затем эти кластеры начинают объединять; при этом на каждом шаге кластеризации объединяются наиболее близкие друг к другу кластеры. Новые полученные образования представляют собой кластеры более высокого уровня в иерархии кластеров, именно поэтому такие методы часто называют методами иерархической кластеризации. Процесс кластеризации обязательно заканчивается за конечное число шагов, так как в итоге все данные оказываются объединенными в один-единственный кластер, совпадающий со всей исходной эмпирической выборкой. Таким образом, в агломеративных методах кластеризация начинается с множества одноэлементных кластеров, соответствующих отдельным эмпирическим данным, а заканчивается получением одного глобального общего кластера. В дивизивных методах все происходит в обратном порядке: один общий глобальный кластер, соответствующий всей эмпирической выборке, постепенно разделяется на все большее число более мелких кластеров. Предельные ограничения этого процесса задает количество элементов в исходной выборке: действительно, максимальное количество отдельных кластеров не может превосходить количества элементов в этой выборке. Однако чаще исследователь сам задает количество кластеров, на которые надо разделить выборку, исходя из каких-либо дополнительных соображений, диктуемых особенностями постановки исследования. 11.4. Классификация иерархических агломеративных Если исследователь решил применять иерархическую агломеративную кластеризацию (и выполнил все предыдущие этапы процедуры кластерного анализа), то далее ему необходимо решить вопрос о выборе конкретного способа определения межкластерных расстояний. Здесь у некоторых читателей может возникнуть вопрос: зачем снова возвращаться к расстояниям, когда мы уже рассматривали их в разделе 11.2? Но дело в том, что в кластерном анализе расстояние рассматривается в двух смыслах: 1) как расстояние между объектами внутри кластера (выбор таких расстояний и рассматривался в разделе 11.2), 2) как расстояние между различными кластерами, получаемыми в процессе кластеризации, или, другими словами, как межкластерное расстояние. На практике это означает, что при решении задачи кластерного анализа конкретных психологических данных исследователь должен, помимо метрики пространства данных и глобальной стратегии кластеризации, выбрать и наиболее подходящий способ определения межкластерных расстояний. Причем, на самом деле, проблема эта – общая как для дивизивных, так и для агломеративных; как для иерархических, так и для итеративных методов кластеризации. Однако для наиболее популярного представителя итеративных дивизивных методов, реализованного во всех рассматриваемых нами статистических пакетах анализа данных, - метода k -средних, выбор способа определения межкластерных расстояний скрыт от пользователя (он «заложен» в самом методе). А вот при использовании иерархической агломеративной кластеризации пользователь должен в явном виде выбрать такой способ из значительного количества предлагаемых. В каждом достаточно развитом статистическом пакете для этого имеются соответствующие возможности, однако сами наборы способов определения межкластерных расстояний, включенные в тот или иной пакет, могут отличаться. Наиболее употребительными способами определения межкластерного расстояния, одновременно используемыми как названия соответствующих методов иерархической агломеративной кластеризации, являются следующие: · Single linkage, nearest neighbor (Простая связь, или метод «ближнего соседа») – расстояние между двумя кластерами определяется как попарное расстояние между двумя самыми ближними друг к другу представителям каждого из них. Метод простой связи сильно сжимает исходное признаковое пространство и рекомендуется для получения минимального «дерева» объединения [3. С.213]. · Complete linkage, furthest neighbor (Полная связь, или метод «дальнего соседа») – расстояние между двумя кластерами определяется по самым дальним друг от друга представителям каждого из них. Этот метод сильно растягивает исходное пространство. · Unweighted pair-group average (Невзвешенная попарно-групповая средняя) – расстояние между двумя кластерами определяется как среднее по всем попарным расстояниям между представителями первого и второго кластеров. Этот метод сохраняет метрику исходного пространства. · Ward's method (Метод Уорда) – расстояние между двумя кластерами определяется по особой формуле. Метод Уорда сильно изменяет метрическое признаковое пространство и за счет этого позволяет получить резко отличающиеся отчетливо выраженные кластеры. Этот метод хорошо применять для выявления трудноуловимых различий, но при этом всегда существует опасность выдать желаемое за действительное, то есть усмотреть наличие «естественного» разбиения эмпирической выборки на определенные группы там, где его на самом деле нет (точнее, где оно носит случайный характер и не будет повторено при измерениях на другой аналогичной эмпирической выборке испытуемых). Существует множество других методов иерархической агломеративной кластеризации, фигурирующих в статистических пакетах под следующими названиями: Weighted pair-group average (Взвешенная попарно-групповая средняя), Unweighted pair-group centroid (Невзвешенная попарно-групповая центроидная); Weighted pair-group centroid (median) (Взвешенная попарно-групповая центроидная (медианная), Between-groups linkage (Межгрупповое связывание), Within-groups linkage (Внутригрупповое связывание), Centroid clustering (Центроидная кластеризация), Median clustering (Медианная кластеризация) и другие. Подробнее методы определения межкластерных расстояний, рассматриваются в источниках [2; 4; 5; 9; 17; 22]. При решении конкретной психологической задачи выбор локальной стратегии кластеризации часто не является очевидным. В этом случае исследователю рекомендуется параллельно применять ряд различных стратегий кластеризации и решать вопрос о предпочтительной стратегии, исходя из получаемых результатов: их непротиворечивости, легкости их теоретической интерпретации и ее соответствия выбранной теоретической концепции исследования. Применение к решению задач, возникающих в психологических исследованиях, агломеративных и дивизивных методов кластеризации, реализованных в рассматриваемых в рамках пособия статистических пакетах, будет проиллюстрировано в следующем разделе. 11.5. Применение методов кластерного анализа Итак, для исследователя-психолога основным делением всевозможных методов кластерного анализа является их деление на агломеративные (объединительные) и дивизивные (разделительные). На практике выбор глобальной стратегии кластеризации часто определяется степенью исследованности рассматриваемого психологического явления: так, при разведочном (эксплораторном) анализе, когда исследователь только начинает изучение данного явления и испытывает дефицит достоверной информации, чаще выбирают агломеративную стратегию, чтобы по ее результатам попытаться определить, на какое именно количество кластеров целесообразно разделять полученные данные. Таким образом, применение агломеративных стратегий кластеризации иногда позволяет исследователю определить количество кластеров, которое будет использоваться при дальнейшем применении дивизивных стратегий в ходе конфирматорного (уточняющего) анализа. В то же время, иногда это количество кластеров определяется из содержательных особенностей задачи, априорно известных исследователю. Важно подчеркнуть, что при любой стратегии и при любом методе полученная кластеризация будет относиться лишь к данной конкретной эмпирической выборке. Вопрос о том, насколько эта выборка репрезентативна и, соответственно, насколько полученные результаты кластеризации могут быть распространены на всю генеральную совокупность, выходит за рамки кластерного анализа и должен исследоваться отдельно: с помощью дискриминантного анализа, методов проверки статистических гипотез, общих принципов экспериментальной психологии (получения репрезентативной выборки эмпирических данных, определения ее необходимого объема, обеспечения валидности и надежности эксперимента и др.). Таким образом, в отличие от методов проверки статистических гипотез, кластерный анализ в определенном смысле является циклической и, в этом плане, незавершенной процедурой анализа данных: его результаты часто имеют эвристический характер и, соответственно, не имеют под собой достаточных статистических оснований, поэтому в любой момент исследования эти результаты могут быть подвергнуты сомнению (под влиянием каких-либо открывшихся новых обстоятельств), что, в свою очередь, может потребовать повторного проведения кластерного анализа с использованием иных методов кластеризации. Такой призыв к осторожности при использовании результатов кластерного анализа остается, однако, не услышанным и не воспринятым значительным количеством современных исследователей-психологов: результаты кластерного анализа нередко выдаются за окончательные и единственно возможные, при этом никакого обсуждения их устойчивости, сравнительного анализа применения различных стратегий кластеризации и т.п., как правило, не приводится. Такова сложившаяся научная практика в нашей стране, однако, начинающему исследователю важно понимать ее неправомерность, а также связанную с ней возможность радикального изменения выводов экспериментального исследования, вызванную даже небольшим изменением используемых кластеризационных процедур. На это обстоятельство справедливо обращают внимание и другие авторы, подчеркивая, что различные кластерные методы вполне могут приводить к различным результатам кластеризации одних и тех же эмпирических данных (см., например, [5. С.188-191]). Обобщая результаты проведенного теоретического рассмотрения, можно сформулировать следующий практический алгоритм применения кластерного анализа в психологическом исследовании при использовании статистических пакетов программ: Шаг 1. Определить типы всех измерительных шкал, примененных для получения выборки эмпирических данных. Ответить на следующие вопросы: Применяются ли интервальные, порядковые, номинальные, дихотомические шкалы? Все ли используемые шкалы однотипны, или имеет место ситуация применения смешанных шкал? Шаг 2. Опираясь на исследовательский опыт, наметить план процедуры кластеризации, в зависимости от которого выбрать подходящий статистический пакет анализа данных, содержащего намеченный метод кластерного анализа. Шаг 3. Запустить пакет и ввести эмпирические данные в предлагаемую таблицу исходных данных, задав соответствующие названия и другие параметры переменных и сформировав, тем самым, матрицу «объект-признак». Шаг 4. В представленном в пакете блоке кластерного анализа последовательно выбрать направление кластеризации, меру сходства или различия для построения метрического пространства данных, глобальную стратегию кластеризации, адекватный конкретный метод кластерного анализа. Шаг 5. Выполнить запланированную и подготовленную процедуру кластеризации. Провести анализ и психологическую интерпретацию полученных результатов, осуществить дополнительную проверку их принципиальной правильности с использованием других методов кластеризации, другого статистического пакета и т.д. Сравнение предложенного алгоритма с общей схемой процедуры применения кластерного анализа в психологическом исследовании позволяет лучше понять распределение эргатических функций между исследователем (человеком) и статистическим пакетом (компьютером, машиной), заставляет задуматься над проблемами грамотного эргономического проектирования автоматизированного рабочего места психолога. Разумеется, на практике действия психолога могут отличаться от приведенной канонической схемы: например, ниже мы специально рассмотрим пример задачи кластеризации, когда (из-за наличия разнотипных шкал и необходимости применения коэффициента Гауэра) вместо матрицы «объект-признак» в качестве входных данных процедуры кластеризации нам придется использовать рассчитанную заранее матрицу попарных расстояний между объектами. Рассмотрим примеры применения агломеративных и дивизивных методов кластеризации в статистических пакетах Statistica for Windows, SPSS и Stadia. Задача 11.5-1. Агломеративная кластеризация для эксплораторного Условие: В целях разработки рекомендаций по повышению психологической готовности к профессиональной деятельности и по оптимальной расстановке кадров проведено исследование менеджеров среднего звена торгово-коммерческой фирмы. Определялись три характеристики: УПМ - уровень профессиональной мотивации (по опроснику профессиональной мотивации со шкалой 20-80), а также уровни УОИ - общего интеллекта и УК - коммуникабельности (по шкале стэнов с использованием соответствующих субшкал опросника 16-PF Р.Кеттелла). Результаты приведены в табл. 11.5-1. Определить: можно ли классифицировать испытуемых на группы со сходными психологическими характеристиками, и, если можно, – то, сколько таких однородных групп целесообразно выделить? Таблица 11.5-1 Дата добавления: 2015-01-18 | Просмотры: 2951500 | Нарушение авторских прав |





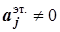
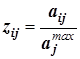



 - нормированное значение элемента
- нормированное значение элемента  матрицы
матрицы - среднее значение элементов по
- среднее значение элементов по  –тому столбцу матрицы
–тому столбцу матрицы по всем подвергнутым измерению
по всем подвергнутым измерению ;
; - среднее квадратическое отклонение, вычисленное по
- среднее квадратическое отклонение, вычисленное по  ,
,  ,
,  - соответственно, наибольшее, наименьшее
- соответственно, наибольшее, наименьшее , имеющих координаты
, имеющих координаты  , где каждое число
, где каждое число  есть результат измерения i -того объекта по j -тому признаку. Другими словами, в таком представлении точки – это объекты; каждый из них имеет столько координат, сколько измерялось признаков; каждая точка соответствует одной строке матрицы «объект-признак».
есть результат измерения i -того объекта по j -тому признаку. Другими словами, в таком представлении точки – это объекты; каждый из них имеет столько координат, сколько измерялось признаков; каждая точка соответствует одной строке матрицы «объект-признак». , имеющих координаты
, имеющих координаты  , где каждое число
, где каждое число  есть результат измерения j -того признака у i -того объекта. Здесь точки – это признаки, и каждый из них имеет столько координат, сколько измерялось объектов; при этом каждая точка соответствует одному столбцу матрицы «объект-признак».
есть результат измерения j -того признака у i -того объекта. Здесь точки – это признаки, и каждый из них имеет столько координат, сколько измерялось объектов; при этом каждая точка соответствует одному столбцу матрицы «объект-признак». – это пространство, состоящее из некоторых объектов, называемых точками (или элементами)данного
– это пространство, состоящее из некоторых объектов, называемых точками (или элементами)данного ), между которыми
), между которыми , называемая метрикой, определенная на всех упорядоченных парах точек множества
, называемая метрикой, определенная на всех упорядоченных парах точек множества  :
: . (11.2-2)
. (11.2-2) . (11.2-3)
. (11.2-3) . (11.2-4)
. (11.2-4) . (11.2-5)
. (11.2-5)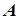 (см. формулу 11.2-1) к матрице
(см. формулу 11.2-1) к матрице  попарных расстояний между эмпирическими точками (в рассматриваемом случае – между объектами) построенного метрического пространства, представленной следующим соотношением:
попарных расстояний между эмпирическими точками (в рассматриваемом случае – между объектами) построенного метрического пространства, представленной следующим соотношением: . (11.2-6)
. (11.2-6) ;
; этой матрицы представляет собой расстояние между точками с номерами
этой матрицы представляет собой расстояние между точками с номерами  и
и  для любых элементов
для любых элементов  для любого номера
для любого номера 



 - объекты из эмпирической выборки данных;
- объекты из эмпирической выборки данных; - значение меры различия d для объектов
- значение меры различия d для объектов  и
и  ;
; - значение меры сходства s для объектов
- значение меры сходства s для объектов  - результаты измерения k -того признака у объектов
- результаты измерения k -того признака у объектов  - соответственно, значение вклада в меру сходства между
- соответственно, значение вклада в меру сходства между