|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Analysis of Variance (clust_1.sta)Between Within signif.
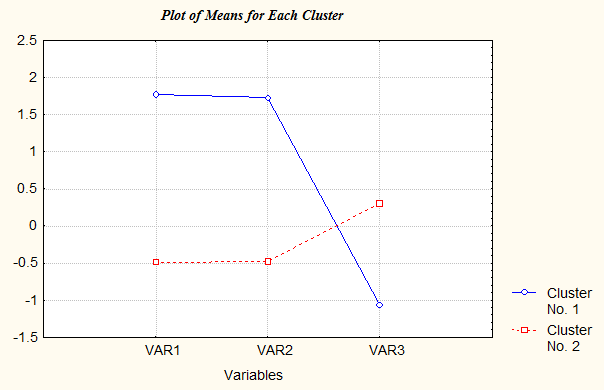
Кнопка Graph of Means (График средних значений) позволяет наглядно представить средние значения переменных по каждому кластеру на одном графике (рис. 11.5-5). Из графика видно, что в первый кластер вошли высоко мотивированные и высокоинтеллектуальные менеджеры, у которых, однако, низкий уровень коммуникабельности. Во второй кластер, напротив, вошли менеджеры, обладающие сравнительно высокой коммуникабельностью, но низкими мотивацией и уровнем общего интеллекта.
Рис. 11.5-5. Графики средних значений переменных Кнопка Members of each Cluster and Distances (Элементы каждого кластера и их расстояния до центра кластера) позволяет выяснить, что первый кластер включает всего 7 случаев, а второй – 25. В связи с этим возникает вопрос: нельзя ли уточнить классификацию, детализовав состав второго кластера? Попробуем сделать это, проведя разбиение не на два, а на три кластера. 4. Возвращаемся в окно «Cluster Analysis: K-Means Clustering» и изменяем значение поля Number of Clusters (Число кластеров) на «3». Нажав ОК, выполняем кластеризацию. В окне просмотра ее результатов K-means Clustering Results видим следующие результаты анализа рассеяния и средних значений: Analysis of Variance (clust_1.sta) Between Within signif.
Members of Cluster Number 1 (clust_1.sta) and Distances from Cluster contains 7 cases (Кластер содержит 7 случаев)
Members of Cluster Number 2 (clust_1.sta) and Distances from Cluster contains 11 cases (Кластер содержит 11 случаев)
Members of Cluster Number 3 (clust_1.sta) and Distances from Cluster contains 14 cases (Кластер содержит 14 случаев)
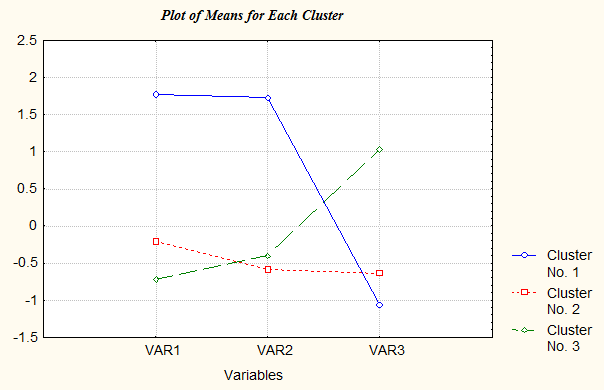
Рис. 11.5-6. Графики средних значений переменных Из рис. 11.5-6 видно, что средние значения для первого кластера принципиально не изменились, а вот второй и третий кластеры представляют собой менеджеров с невысокой мотивацией и уровнем интеллекта, но с принципиально разными коммуникативными способностями. Количество испытуемых в кластерах получилось следующее: в первом – 7, во втором – 11, в третьем – 14. Таким образом, нам удалось «расслоить» менеджеров с низкой мотивацией на два кластера, в одном из которых (в третьем) стала очевидной стратегия психологического сопровождения деятельности, направленная на повышение профессиональной мотивации. Этот результат «оправдывает» увеличение числа кластеров в разбиении с двух до трех. Однако возникает вопрос: нельзя ли и далее детализировать полученные группы с целью дальнейшей дифференциации мер психологического сопровождения деятельности и данных для подбора и расстановки кадров? Чтобы ответить на него, выполним кластеризацию еще раз, но уже – с разбиением на 4 кластера. 5. Для четырех кластеров получим следующие результаты:
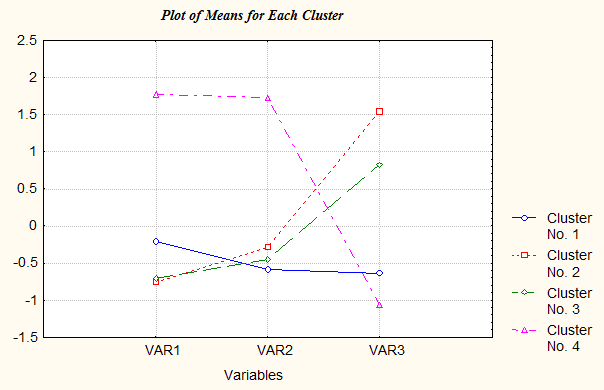
Рис. 11.5-7. Графики средних значений переменных Analysis of Variance (clust_1.sta) Between Within signif.
Из рис. 11.5-7 видно, что по сравнению с разбиением на три группы первый и второй кластеры принципиально сохранились, а третий «расслоился» на два, отличающиеся друг от друга не принципиально, а лишь конкретным уровнем интеллекта и коммуникабельности. Таким образом, никакой принципиально новой информации разбиение на 4 кластера нам не принесло. Ответ: данную выборку можно разделить на 2, 3, 4 и т.д. кластеров, достоверно отличающихся друг от друга, но из содержательных соображений целесообразно разделить выборку на три кластера. Задача 11.5-3. Выявление кластеров эмпирической выборки Условие: Решить задачи 11.5-1 и 11.5.-2, используя пакет SPSS. Решение: 1. Запускаем пакет SPSS и вводим данные (табл. 11.5-1) по трем переменным в отдельные столбцы. 2. Выполняем стандартизацию данных. Для этого: · в пункте меню Statistics (Статистики) выбираем команду Summarize (Подытожить) и, далее, Descriptives (Описательные статистики); · в открывшемся диалоговом окне задаем Variables (Переменные) – var00001, var00002, var00003; · устанавливаем флажок в поле Save standardized values as Variables (Сохранить стандартизованные величины как переменные) и нажимаем кнопку ОК. В окне SPSS viewer (Просмотр результатов) можно просмотреть показатели описательной статистики, однако сейчас они нас не интересуют. Главное, что в окне редактора данных SPSS Data editor появились три новые стандартизованные переменные с именами zvar00000, zvar00001, zvar00002. Теперь исходные данные можно удалить, а стандартизованные переменные – переименовать, присвоив им названия var1, var2, var3. Сохраним введенные данные в файле с названием clust_2.sav. 3. Выполним агломеративную кластеризацию. Для этого: · В пункте меню Statistics (Статистики) последовательно выберем команды Clussify (Классифицировать) и Hierarchical Cluster (Иерархический кластер). · В открывшемся диалоговом окне Hierarchical Cluster Analysis (Иерархическая кластеризация) задаем Variables (Переменные) – var1, var2, var3, а также устанавливаем флажок опции Cluster (Кластер) в поле Cases (Случаи). · Нажав на кнопку Plots… (Графики…), в открывшемся диалоговом окне устанавливаем флажок в поле Dendrogram (Дендрограмма). После этого нажимаем на кнопку Continue (Продолжить) и возвращаемся в основное окно метода. · Нажав на кнопку Method (Метод), в открывшемся диалоговом окне выбираем метод кластеризации и метрику. Как и в пакете Statistica for Windows, в SPSS для проведения агломеративной кластеризации реализован широкий (хотя и отличающийся) набор мер различия (сходства) и методов (их обсуждение см. в разделах 11.2 - 11.4). Выбираем здесь метод Nearest neighbor (Ближайшего соседа), Measure (Мера) – Interval (Интервальная шкала), Euclidean Distance (Евклидово расстояние). В блоке Transform values (Преобразование величин) можно было бы задать стандартизацию, однако мы ее уже выполнили. Таким образом, пакет SPSS имеет богатые возможности по применению преобразований данных, метрик и методов кластеризации. Нажав кнопку Continue (Продолжить), возвращаемся в предыдущее окно. · Нажимаем кнопку Statistics (статистики). Оставляем заданный по умолчанию флажок в поле Agglomeration schedule (Порядок объединения). Кроме того, в этом окне имеется возможность задать фиксацию принадлежности к кластерам, причем сразу для целого диапазона решений. Для этого используется блок Cluster Membership (Принадлежность к кластерам). Ставим флажок в поле Rang of solutions (Диапазон решений) и задаем этот диапазон, указав значения: From (От) – «2» и Trough (До) – «4». · Нажав Continue (Продолжить), возвращаемся в основное окно метода и нажимаем OK для выполнения собственно кластеризации. 4. В окне SPSS viewer (Просмотр результатов) видны результаты кластеризации и, в частности, Dendrogram (Дендрограмма) (рис. 11.5-8), имеющая принципиально тот же вид, что и при использовании пакета Statistica for Windows (см. рис.11.5-1 – 11.5-4). Кроме того, здесь приведена таблица Agglomeration Schedule (Порядок объединения), а также показанная ниже таблица Cluster Membership (Принадлежность к кластерам) (для выбранного нами диапазона решений).
* * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * *
Dendrogram using Single Linkage
Rescaled Distance Cluster Combine
C A S E 0 5 10 15 20 25 Label Num +---------+---------+---------+---------+---------+
13 -+-+ 31 -+ +-+ 16 -+-+ I 28 -+ I +-+ 15 ---+ I I 5 ---+-+ +-----+ 11 ---+ I I 18 -------+ +-+ 9 -+-----+ I I 21 -+ +-----+ +---+ 19 -------+ I +---------+ 20 ---------------+ I I 2 -------+-----------+ I 8 -------+ I 3 -+-+ +-------------------+ 30 -+ +-+ I I 27 ---+ +---------------+ I I 25 -----+ I I I 14 -+-----------+ +-------+ I 24 -+ I I I 17 ---+-+ +-------+ I 23 ---+ I I I 32 -----+-------+ I 7 -----+ I I 29 -------------+ I 4 ---+ I 10 ---+-------------------+ I 1 ---+ +-------------------------+ 22 ---+---------------+ I 26 ---+ +---+ 6 -----+-------------+ 12 -----+ Рис.11.5-8. Дендрограмма агломеративной кластеризации Cluster Membership
Cluster Membership (продолжение)
5. Выполним дивизивную кластеризацию методом k -средних. Для этого в пункте главного меню Statistics (Статистики) выбираем команду Clussify (Классифицировать) и, далее, K-Means Cluster Analysis (Кластерный анализ методом k -средних). 6. В открывшемся диалоговом окне метода: · задаем Variables (Переменные) – var1, var2, var3; · устанавливаем флажок опции Method (Метод) в поле Iterate and classify (Итерировать и классифицировать); · задаем Number of Clusters (Количество кластеров), равное двум; · в поле Maximum iterations (Максимальное число итераций) указываем, например, «20» (это число задается в пределах от 1 до 999); · оставляем предлагаемое по умолчанию значение «0» для поля Convergence criterion (Критерий сходимости): этот критерий принимает значение от 0 до 1, понимаемое как процент от минимального расстояния между начальными центрами кластеров, и определяет, что итерации прекращаются, когда очередная из них не перемещает ни один из центров кластеров на расстояние большее, чем указано в значении критерия. · все остальные многочисленные возможные параметры метода не изменяем, так как в этом нет необходимости. 7. Выполнив кластеризацию, в окне SPSS viewer (Просмотр результатов) видим итоги разделения, соответственно, на два, три и четыре кластера, включающие таблицы Final Cluster Centers (Окончательные центры кластеров), Cluster Membership (Принадлежность к кластерам), Number of Cases in each Cluster (Количество случаев в каждом кластере) и ANOVA (Результаты проверки качества разбиения с помощью ANOVA), выборочно представленные ниже. Для двух кластеров: ANOVA
Number of Cases in each Cluster
Для трех кластеров: Cluster Membership
ANOVA
Number of Cases in each Cluster
Для четырех кластеров: ANOVA
Number of Cases in each Cluster
Таким образом, результаты кластеризации получились те же, что и при использовании пакета Statistica for Windows. Ответ: выборку целесообразно разделить на 2, 3 или 4 кластера. Предпочтительный выбор одного из этих вариантов должен определяться либо из содержательных соображений, либо за счет увеличения объема выборки и проведения повторной кластеризации. Задача 11.5-4. Применение кластерного анализа к данным, Условие: Коммерческая организация объявила о приеме на работу молодых людей в возрасте от 18 до 25 лет, имея ряд разнородных вакансий. Претенденты, обратившиеся в отдел кадров, заполняли бланки нескольких опросников. Сводные результаты приведены в табл. 11.5-2, в которой используются следующие обозначения ТП – тип профессии - результат определения предпочтительной ЧЗ – «человек – знак», ЧП – «человек – природа», ЧХО – «человек – художественный образ», ЧТ – «человек – техника», ЧЧ – «человек – человек»; УГР – уровень готовности к риску по опроснику готовности СР - склонен к риску, СУ - средний уровень, СО - слишком осторожен; УМД – уровень мотивации достижения по опроснику мотивации ЛК – локус контроля по пункту 8 («В определении трудностей К – на понимание и снисходительность коллег, С – на себя, Р – на помощь родителей, СВ – на советы сверстников, РД – на заинтересованность во мне работодателя ВР – возраст (полных лет); П – пол (М – мужской, Ж – женский). Определить: на какие группы можно разделить претендентов по признаку сходства показанных ими результатов. Таблица 11.5-2 Дата добавления: 2015-01-18 | Просмотры: 1199 | Нарушение авторских прав |