АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

Показатели личностных свойств менеджеров

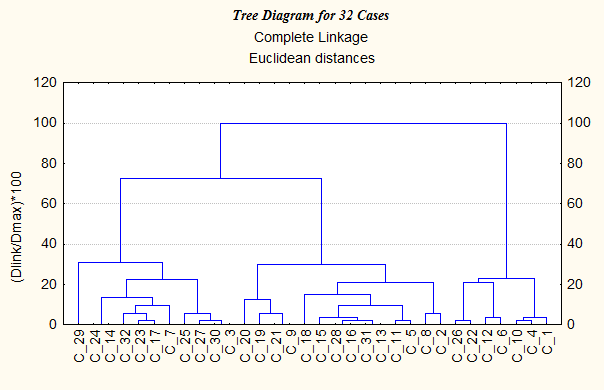
Решение:

Исследовательская ситуация, отраженная в задаче, относится к эксплораторному анализу, так как у психолога не имеется априорной информации о количестве кластеров, на которые следует разделять выборку данных. В связи с этим на первом этапе решения целесообразно применить иерархическую агломеративную стратегию кластеризации, которая может помочь выявить естественное количество кластеров, характерное для данной выборки.

Для агломеративной кластеризации можно применить любой из статистических пакетов SPSS, Statistica for Windows и Stadia, что мы и сделаем в дальнейшем, чтобы продемонстрировать их возможности и проблемы, с которыми сталкивается исследователь на практике. Начнем с пакета Statistica for Windows, в котором нагляднее реализовано графическое представление получаемой дендрограммы.

1. Запускаем пакет Statistica for Windows и в его переключателе модулей первоначально выбираем не модуль Cluster Analysis (Кластерный анализ), а модуль Data Management (Управление данными). Потребность в этом обусловлена характером данных: они измерены хотя и в интервальных, но в различных по масштабу шкалах; в связи с чем необходимо выполнить их стандартизацию.

2. В пункте меню File (Файл) выбираем команду New data (Новые данные). В открывшемся диалоговом окне Create new file (Создать новый файл) задаем необходимые параметры:

· New File Name (Имя нового файла) – например, clust_1 (от слова cluster – кластер). При этом можно задать размещение файла на определенном логическом диске и в нужной папке. Расширение имени «.sta» будет присвоено файлу автоматически.

· Number of Variables (Количество переменных) – зададим соответствующее условиям количество - 3.

· Number of Cases (Количество случаев) – в соответствии с данными задачи зададим 32.

· Case Name Length (Длина имени случая) – оставим здесь предлагаемое по умолчанию значение «0», так как не собираемся использовать «длинные» текстовые имена случаев.

· Value Format (Формат значений) – по умолчанию предлагается формат «8.3», что означает общую длину 8 позиций и 3 позиции на знаки после десятичной запятой. Хотя наши данные – целые, положительные и не более двух знаков, и можно бы было задать формат «2.0», но мы собираемся выполнить стандартизацию, после которой данные могут стать дробными и отрицательными. Поэтому зададим формат «5.2», выбор которого обосновывается следующим образом: в стандартизованных данных мы будем использовать два знака после запятой, один – сама запятая, один – целая часть (которая либо 0, либо 1), еще одна позиция отводится на знак величины, итого общая длина – пять знаков.

· Missing Data Code (Код для пропущенных значений) – оставляем без изменения предлагаемое по умолчанию значение –9999.

· Variable Name Prefix – (Префикс названий переменных) – здесь определяется повторяющаяся часть имен переменных, расположенная перед их номерами. Оставим предлагаемый префикс VAR.

· Variable Name Start Number (Начальный номер имени переменной) – оставим предлагаемое значение «1».

· One-Line File Header (Краткое описание файла) – запишем «Данные для задачи 11.5-1», хотя это поле можно и не заполнять.

3. Вводим исходные данные по субшкалам в отдельные столбцы, соответствующие переменным.

4. В пункте меню Analysis (Анализ) выбираем команду Standardize (Стандартизовать) и в диалоговом окне Standardization of Values (Стандартизация значений) задаем следующие значения параметров:

· Variables (Переменные) – VAR1 - VAR3;

· Cases (Случаи) – All (Все);

· Weight (Вес) – Off (Не задавать).

После нажатия кнопки ОК выполняется стандартизация, и стандартизованные значения переменных записываются в таблицу вместо старых – «сырых» - баллов. Все стандартизованные переменные имеют среднее значение (Mean), равное нулю, и стандартное (среднеквадратическое) отклонение (SD - Standard deviation), равное единице. В этом легко убедиться, дважды щелкнув левой клавишей «мыши» по заголовку переменной и нажав в открывшемся диалоговом окне кнопку Values/Stats (Статистика переменных).

5. Выполнив команды File (Файл) - Save (Сохранить), сохраним результаты стандартизации в созданном нами файле clust_1.sta.

6. В пункте меню Analysis (Анализ) выбираем команду Other St atistics (Другие статистики), вызывающую переключатель модулей пакета Statistica for Windows, и переключаемся в модуль Cluster Analysis (Кластерный анализ). После этого модуль Data Management (Управление данными) можно закрыть, так как мы использовали его только для стандартизации переменных, и больше он нам не понадобится.

7. В пакете Statistica for Windows реализовано три базовых метода кластерного анализа, содержащихся в стартовом окне модуля Cluster Analysis (Кластерный анализ), которое называется Clustering method (Метод кластеризации):

· Joining (Tree Clustering) (Объединение - Дерево кластеризации) – агломеративный метод последовательной иерархической кластеризации;

· K-means Clustering (Кластеризация k -средними) – дивизивный метод кластеризации, направленный на разделение исходного множества объектов на заранее заданное количество кластеров k;

· Two-way Joining (Двунаправленное объединение) – метод, при котором кластеризация проводится одновременно и по объектам (случаям), и по переменным (признакам) [41].

В данном случае нас интересует агломеративная кластеризация, поэтому выбираем метод Joining (Tree Clustering) (Объединение – «Дерево» кластеризации).

8. При входе в стартовое меню данного метода исследователь последовательно заполняет следующие поля:

· Variables (Переменные) – выбираем здесь используемые переменные VAR1, VAR2, VAR3.

· Input (Тип входных данных) – выбираем способе представления данных. здесь есть два варианта: а) матрица «объект-признак», или Raw data (Исходные данные), б) Distance matrix (Матрица расстояний). Мы выбираем вариант а) – Raw data (Исходные данные).

· Clusters (Кластеры) - здесь в смысле того, что именно подвергать кластеризации: а) объекты, на которых проводятся измерения – Cases (Случаи), другими словами – Rows (Строки) исходной матрицы данных, б) измеряемые признаки – Variables (Переменные), или Columns (Столбцы) исходной матрицы данных. Мы выбираем вариант а) – Cases (Случаи).

· Amalgamation (Linkage) Rule (Правило объединения (связывания)) -– это выбор способа определения межкластерного расстояния (см. раздел 11.3). Здесь у исследователя имеется значительное количество возможностей, из которых выберем для начала вариант Single Linkage (Одиночная связь).

· Distance Measures (Мера расстояния, метрика) – в этом поле выбирается мера сходства или различия. Выбираем вариант Distance Measures (Меры расстояния). Здесь предлагается ряд возможностей (см. раздел 11.2). Поскольку наши данные – интервальные, выберем вариант Euclidean distance (Евклидово расстояние).

· Missing Data Deletion (Способ обработки пропущенных значений) - выберем Casewise deletion of missing data (Удаление отсутствующих данных); второй возможный вариант здесь - Substitution by Means (Замена средними значениями).

9. После нажатия ОК выполняется кластеризация, и открывается диалоговое окно ее результатов Joining Results. Установим здесь флажки в поля Rectangular branches (Прямоугольная дендрограмма) и Scale tree to dlink/dmax*100 (Процентная шкала дендрограммы), которое определяет нормирование шкалы дендрограммы: расстояние, на котором произведено объединение кластеров, делится на максимальное межкластерное расстояние, и результат переводится в проценты.

10. Смотрим полученную дендрограмму, например, в вертикальном виде, нажав для этого соответствующую кнопку Vertical Icicle Plot (Вертикальный график). На дендрограмме отчетливо просматривается образование трех кластеров (рис. 11.5-1).

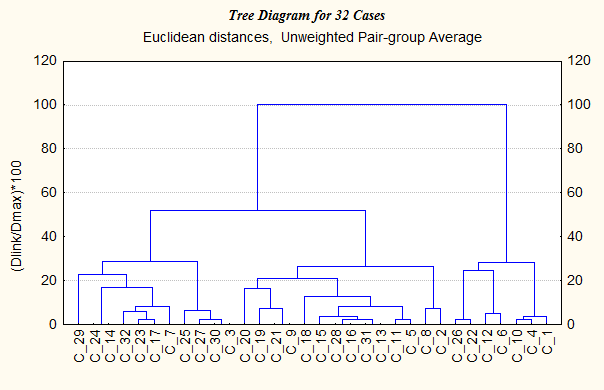
Рис. 11.5-1. Дендрограмма агломеративной кластеризации
методом простой связи

11. Можно просмотреть и другие результаты кластеризации: Amalgamation Schedule (Список Объединения), Graph of Amalgamation Schedule (График объединения), Distance Matrix (Матрица расстояний), Descriptive Statistics (Описательная Статистика).

Рассчитанную матрицу расстояний можно сохранить в файле с помощью команды Save Distance Matrix (Сохранить матрицу расстояний), однако в данной задаче эта возможность нас не интересует.

12. Проверяем полученные результаты, применяя другие способы кластеризации: например, Complete linkage (Полная связь), Unweighted pair-group average (Невзвешенная попарно-групповая средняя), Ward's method (Метод Уорда). Дендрограммы, представленные на рис. 11.5-2 - 11.5-4, подтверждают целесообразность разделения выборки именно на три кластера. Можно также попробовать применять другие метрики и убедиться, что для наших данных при изменении метрики результат принципиально не меняется.

Рис. 11.5-2. Дендрограмма агломеративной кластеризации
методом полной связи

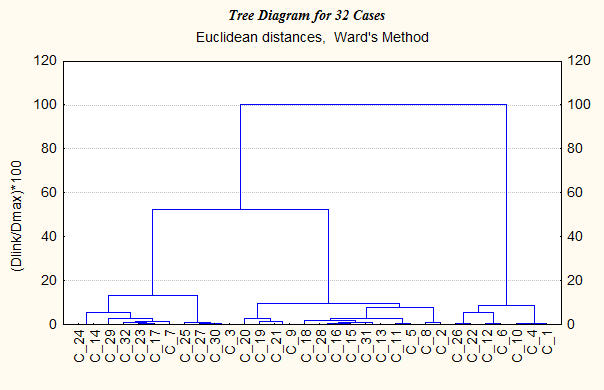
Рис. 11.5-3. Дендрограмма агломеративной кластеризации
методом невзвешенной попарно-групповой связи

Рис. 11.5-4. Дендрограмма агломеративной
кластеризации методом Уорда

Таким образом, вывод об образовании трех кластеров в целом подтверждается, хотя на некоторых дендрограммах заметно образование двух кластеров более высокого порядка. Такая ситуация является характерной для иерархических методов кластеризации: они, как правило, не дают однозначного ответа на вопрос о числе кластеров.

Еще одно важное замечание, которое необходимо сделать, состоит в том, что далеко не всегда результаты кластеризации, полученные разными методами, так качественно похожи, как в данном случае. Нередко встречается ситуация, когда при использовании разных методов исследователь получает разное количество и состав кластеров. В этом случае выбор одного из вариантов опирается на опыт исследователя, его научную интуицию, а также цель исследования и содержательные особенности задачи. Продолжение исследования данной выборки представлено в решении задачи 11.5-2.

Ответ: агломеративная кластеризация позволяет предположить, что данную эмпирическую выборку целесообразно разделять на два, три или четыре кластера.

Задача 11.5-2. Дивизивная кластеризация эмпирической выборки
(с использованием пакета Statistica for Windows)

Условие: в продолжение задачи 11.5.-1 выполнить и обосновать разделение эмпирической выборки на кластеры.

Решение:

1. После анализа результатов агломеративной кластеризации (см. задачу 11.5-1) переходим к следующему этапу решения задачи – дивизивной кластеризации данных, т.е. разбиению выборки на заданное число кластеров, для которого мы уже определили возможный диапазон: от двух до четырех. Возвращаемся в стартовое окно Clustering method (Метод кластеризации) модуля Cluster Analysis (Кластерный анализ) и выбираем метод K-Means Clustering (Кластеризация k -средними). Этот метод относится к дивизивным (разделительным) и позволяет разбить исходное множество данных на фиксированное количество кластеров.

2. В диалоговом окне этого метода «Cluster Analysis: K-Means Clustering» заполняем следующие поля:

· Variables (Переменные) – определяем здесь набор переменных, участвующих в кластеризации: это VAR1, VAR2, VAR3.

· Cluster Cases or Variables (Что подвергать кластеризации – случаи или переменные) – выбираем Cases-Rows (Случаи-Строки).

· Number of Clusters (Число кластеров) – для начала в качестве требуемого числа кластеров задаем значение «2».

· Maximum number of iterations (Максимальное число итераций) – здесь можно указать максимальное число итераций кластеризационной процедуры (от 5 до 99), иначе в некоторых случаях вычисления могут продолжаться бесконечно. Установим, например, значение «15».

· Missing Data Deletion (Способ обработки ошибочных или пропущенных значений) - выберем Casewise deletion of missing data (Удаление пропущенных данных);

· Флажок в поле Batch Processing and Printing (Одновременная кластеризация и вывод на печать) задавать не будем, т.е. оставим это поле пустым.

3. Нажав на кнопку ОК, выполняем кластеризацию. Открывается окно просмотра ее результатов K-means Clustering Results, в котором указано, что решение получено после одной итерации. Для просмотра и сохранения результатов предлагается ряд экранных кнопок:

· Analysis of Variance (Анализ рассеяния),

· Means of each Cluster & Distances (Средние значения переменных для каждого кластера и расстояния),

· Graph of Means (График средних значений),

· Descriptive Statistics for each Cluster (Описательная статистика для каждого кластера),

· Members of each Cluster and Distances (Элементы каждого кластера и их расстояния до центра кластера),

· Save Classifications & Distances (Сохранить классификацию и расстояния).

Рассмотрим наиболее важные результаты.

Кнопка Analysis of Variance (Анализ рассеяния) позволяет проанализировать значимость различий между средними значениями каждой переменной по всем кластерам, для выявления которой используется F -критерий Фишера; вычисление его статистики F основано на межгрупповой дисперсии (Between SS), внутригрупповой дисперсии (Within SS) и количестве степеней свободы (df). Полученные результаты (здесь и далее они округлены до второго, а для уровня значимости – до третьего знака после десятичной запятой), представлены следующим образом:

Дата добавления: 2015-01-18 | Просмотры: 1208 | Нарушение авторских прав