 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегрирование методом замены переменной и по частямМетод замены переменной (метод подстановки) – наиболее общий метод, часто применяемый при вычислении интегралов. Им часто приходится пользоваться и для того, чтобы получить табличный интеграл из справочника. Состоит он в том, что при вычислении
вместо переменной х вводится новая переменная t по формуле
Для доказательства этой формулы достаточно вычислить дифференциалы от каждой ее части. Имеем
Таким образом, для вычисления интеграла (2.1) методом замены переменной нужно не только в функции Заметим, что формулу (2.2) часто применяют справа налево, то есть записывают ее в виде
Если
В частном случае, когда
откуда
Примеры. Вычислим интегралы: 1) Решение. 1) 2) 3) Выведем теперь формулу интегрирования по частям. Пусть
откуда
Интегрируя обе части последнего равенства и учитывая, что для
Формула (2.4) и называется формулой интегрирования по частям. Она позволяет свести вычисление интеграла Примеры. Вычислим интегралы: 1) Решение. 1) 2) При вычислении интегралов методом интегрирования по частям важно уметь правильно выбирать u и dv. Общий принцип состоит в том, что получающийся интеграл должен быть проще исходного интеграла. Укажем некоторые классы интегралов, которые вычисляются методом интегрирования по частям. I. II. III. IV. V. Пример. Вычислим интеграл Решение. Дата добавления: 2015-01-18 | Просмотры: 729 | Нарушение авторских прав |
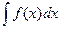 (2.1)
(2.1)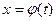 , причем
, причем 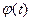 подбирается так, чтобы после подстановки получилась подынтегральная функция, более удобная для интегрирования. При этом справедлива формула
подбирается так, чтобы после подстановки получилась подынтегральная функция, более удобная для интегрирования. При этом справедлива формула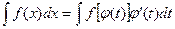 . (2.2)
. (2.2)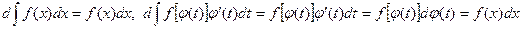 . Дифференциалы равны, поэтому обе части равенства представляют собой одно и то же семейство первообразных для функции
. Дифференциалы равны, поэтому обе части равенства представляют собой одно и то же семейство первообразных для функции 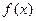 , то есть формула (2.2) имеет место.
, то есть формула (2.2) имеет место.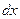 выразить через t и
выразить через t и 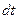 , то есть положить
, то есть положить 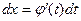 . В результате вычисления получим функцию от переменной t. Чтобы возвратиться к переменной х, достаточно в полученной функции заменить t значением
. В результате вычисления получим функцию от переменной t. Чтобы возвратиться к переменной х, достаточно в полученной функции заменить t значением 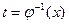 , где
, где 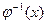 – обратная к
– обратная к 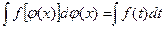 , где
, где 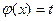 . (2.3)
. (2.3)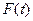 – первообразная для функции
– первообразная для функции 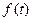 , то есть
, то есть 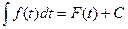 , то из (2.3) получаем
, то из (2.3) получаем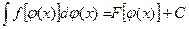 .
.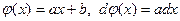 , имеем
, имеем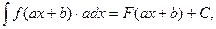
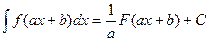 .
.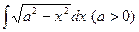 ; 2)
; 2) 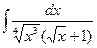 ; 3)
; 3) 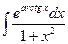 .
.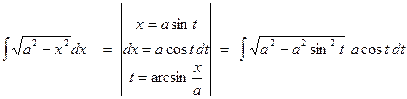 =
= 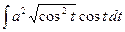 =
= 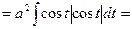 (полагаем
(полагаем 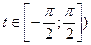 =
= 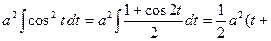
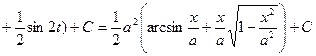 .
.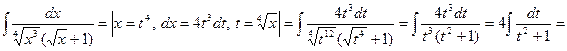
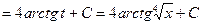 .
.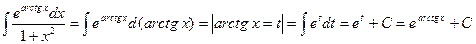 .
.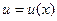 и
и 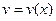 – функции, дифференцируемые на некотором промежутке Х. Тогда
– функции, дифференцируемые на некотором промежутке Х. Тогда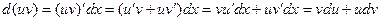 ,
,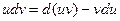 .
.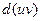 первообразной является uv, получим
первообразной является uv, получим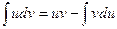 . (2.4)
. (2.4)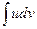 к вычислению интеграла
к вычислению интеграла 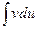 , который может оказаться более простым для интегрирования.
, который может оказаться более простым для интегрирования.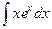 ; 2)
; 2) 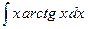 .
.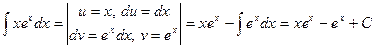 .
.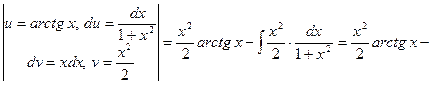
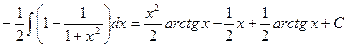 .
.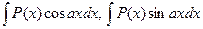 , где
, где 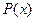 – многочлен; нужно положить
– многочлен; нужно положить 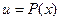 .
.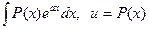 .
.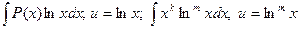 .
.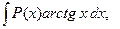
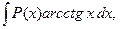
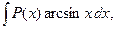
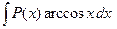 . В каждом из этих интегралов за u берут обратную тригонометрическую функцию.
. В каждом из этих интегралов за u берут обратную тригонометрическую функцию.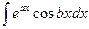 ,
, 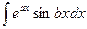 . Нужно дважды применить формулу интегрирования по частям, оба раза взяв за u либо показательную, либо тригонометрическую функцию.
. Нужно дважды применить формулу интегрирования по частям, оба раза взяв за u либо показательную, либо тригонометрическую функцию.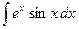 .
.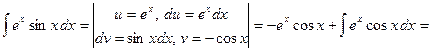
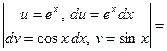
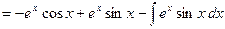 . Отсюда
. Отсюда 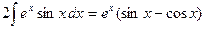 и
и 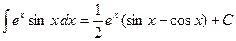 .
.