 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегрирование тригонометрических функцийРассмотрим интегралы вида
Пример 1. Вычислим интеграл Решение. Имеем
Несмотря на то, что универсальная подстановка дает возможность проинтегрировать всякую функцию вида если если если Эти подстановки предпочтительнее универсальной подстановки, поскольку преобразования получаются менее громоздкими. Для преобразования подынтегрального выражения часто применяются различные тригонометрические формулы. В первую очередь применяют формулы
Примеры. Вычислим интегралы: 2) Решение. 2) Преобразуем подынтегральное выражение по одной из приведенных выше формул. Получим 3) Подынтегральная функция
Дата добавления: 2015-01-18 | Просмотры: 700 | Нарушение авторских прав |
 , где R, как и раньше, рациональная функция своих аргументов
, где R, как и раньше, рациональная функция своих аргументов 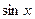 и
и  . Такие интегралы всегда рационализируются с помощью подстановки
. Такие интегралы всегда рационализируются с помощью подстановки  , которая называется универсальной подстановкой. Действительно,
, которая называется универсальной подстановкой. Действительно, ,
, 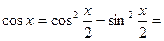
 ,
,  ,
, 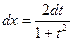 . Поэтому
. Поэтому  − интеграл от рациональной функции. Следовательно, любой интеграл рассматриваемого вида выражается через элементарные функции.
− интеграл от рациональной функции. Следовательно, любой интеграл рассматриваемого вида выражается через элементарные функции. .
.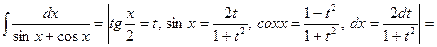
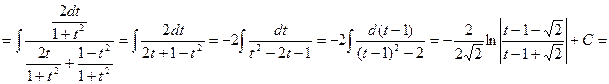
 .
. , на практике она часто приводит к слишком громоздким вычислениям. Во многих случаях проще использовать другие подстановки. В частном случае,
, на практике она часто приводит к слишком громоздким вычислениям. Во многих случаях проще использовать другие подстановки. В частном случае,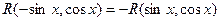 , то
, то  ,
,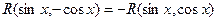 , то
, то  ,
, , то
, то  или
или  .
.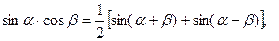
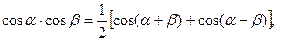

 ,
,  .
.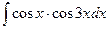 ; 3)
; 3)  .
. .
.
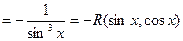 , поэтому нужно сделать подстановку
, поэтому нужно сделать подстановку  . Для вычисления последнего интеграла подынтегральную функцию представим в виде суммы простых дробей, воспользовавшись методом неопределенных коэффициентов (подынтегральная функция – правильная рациональная дробь):
. Для вычисления последнего интеграла подынтегральную функцию представим в виде суммы простых дробей, воспользовавшись методом неопределенных коэффициентов (подынтегральная функция – правильная рациональная дробь):
 ,
, ,
,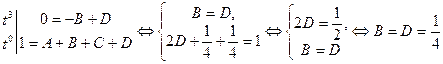 . Значит,
. Значит, 

 .
.