 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Интегрирование рациональных функцийВсегда ли неопределенный интеграл можно выразить через элементарные функции, то есть через степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции с помощью конечного числа арифметических действий и суперпозиций? Производная элементарной функции всегда функция элементарная, для интегралов же это не так. Например, не выражаются через элементарные функции интегралы
В дальнейшем нас будут интересовать такие конкретные классы функций, интегралы от которых выражаются через элементарные функции. Самым важным среди таких классов является класс рациональных функций, то есть функций вида 1) Интегрирование простейших рациональных функций (простых дробей). Простыми дробями называются дроби следующих четырех типов: I. где A, M, N, a, p, q – действительные числа, а квадратный трехчлен I.
II.
III. Выделим из квадратного трехчлена
Положим
Таким образом,
IV. Полагая, как и в предыдущем случае,
Отсюда получаем рекуррентную формулу для вычисления
Поэтому
где Пример 1. Вычислим интеграл Решение. Имеем
По формуле (3.5) при
2) Интегрирование правильных дробей. Рациональная дробь Интегрирование правильных дробей основано на следующей теореме, которую мы сформулируем без доказательства (доказательство см., например, в учебнике Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, т.2, гл. VIII, §2, п. 274; возможно доказательство в курсе алгебры): Теорема. Каждая правильная рациональная дробь может быть представлена в виде суммы конечного числа простых дробей. Это разложение правильной дроби на простые дроби тесным образом связано с разложением ее знаменателя
где
Показатели у знаменателей последовательно уменьшаются от Изложенный метод представления правильной дроби в виде суммы простых дробей называется обычно методом неопределенных коэффициентов. Заметим, что неизвестные коэффициенты из равенства многочленов можно находить и иначе, подставляя вместо х конкретные значения. При этом тоже будут получаться линейные относительно неизвестных коэффициентов уравнения. В качестве значений х удобнее всего брать корни знаменателя. При этом почти все члены в правой части равенства обращаются в нуль, что позволяет легко находить оставшиеся коэффициенты. Можно применять также комбинированный способ отыскания неизвестных коэффициентов, при котором уравнения получаются как приравниванием коэффициентов при одинаковых степенях х, так и подстановкой значений х. Пример 2. Вычислим интеграл Решение. На основании формулы (3.7) имеем:
3. Интегрирование рациональных функций. Пусть Таким образом, интегрирование неправильной дроби сводится к интегрированию многочлена и правильной дроби. Интегрирование правильной дроби сводится, как мы видели, к интегрированию простых дробей. Интегралы от простых дробей есть функции элементарные – рациональные функции, арктангенсы и логарифмы. Поэтому интеграл от любой рациональной функции выражается через элементарные функции – рациональные функции, арктангенсы и логарифмы. Пример 3. Вычислим интеграл Решение. Рациональная дробь целую часть:
 Таким образом, Таким образом,  , причем квадратный трехчлен , причем квадратный трехчлен  действительных корней не имеет. Поэтому действительных корней не имеет. Поэтому
Дата добавления: 2015-01-18 | Просмотры: 782 | Нарушение авторских прав |
 и другие.
и другие.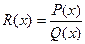 , где
, где 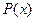 и
и  – многочлены. Интегрирование функций этого класса начнем с рассмотрения простейших случаев.
– многочлены. Интегрирование функций этого класса начнем с рассмотрения простейших случаев.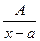 ; II.
; II.  ; III.
; III.  ; IV.
; IV.  , (3.1)
, (3.1) не имеет действительных корней, так что
не имеет действительных корней, так что  , откуда
, откуда  .
. , т.е.
, т.е. , (3.2)
, (3.2) , k = 2, 3, …, то есть
, k = 2, 3, …, то есть . (3.3)
. (3.3)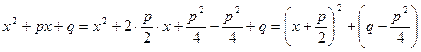 .
. (это можно сделать, так как
(это можно сделать, так как  . Получим
. Получим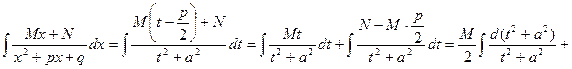
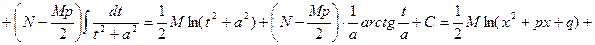
 .
.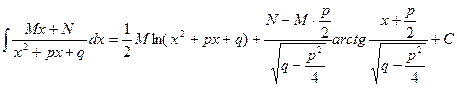 . (3.4)
. (3.4)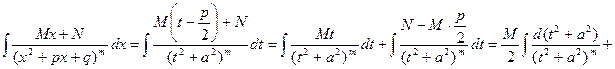
 . К последнему интегралу, который обозначим
. К последнему интегралу, который обозначим 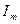 , применим формулу интегрирования по частям:
, применим формулу интегрирования по частям:
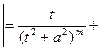


 .
. :
: . (3.5)
. (3.5) ,
, .
. .
. , то есть квадратный трехчлен
, то есть квадратный трехчлен  действительных корней не имеет. Выделим полный квадрат:
действительных корней не имеет. Выделим полный квадрат: 
 . Положим
. Положим  . Тогда
. Тогда
 .
. и
и  получим
получим 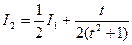 . Поскольку
. Поскольку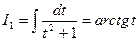 , имеем
, имеем  и
и
 .
. , (3.6)
, (3.6) – действительные корни многочлена
– действительные корни многочлена 
 . (3.7)
. (3.7) до 1,
до 1,  ,от
,от  до 1, от
до 1, от  до 1,
до 1, 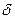 до 1, а
до 1, а  – неопределенные коэффициенты. Чтобы найти эти коэффициенты, нужно дроби в правой части равенства (3.7) привести к общему знаменателю, которым, очевидно, будет многочлен
– неопределенные коэффициенты. Чтобы найти эти коэффициенты, нужно дроби в правой части равенства (3.7) привести к общему знаменателю, которым, очевидно, будет многочлен  на сумму простых дробей. Таким образом, интегрирование правильной дроби
на сумму простых дробей. Таким образом, интегрирование правильной дроби  .
.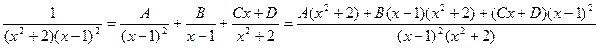 ,
, ,
,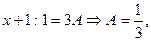
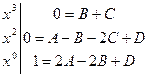
 Поэтому
Поэтому 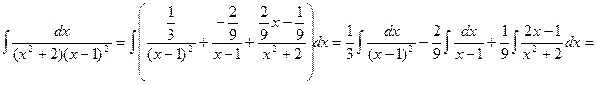
 .
. .
. – неправильная, выделим из нее
– неправильная, выделим из нее
 .
.