|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология
|
Величина, численно равная работе изотермического увеличения поверхности жидкости на единицу, называется коэффициентом поверхностного натяжения
Обозначим 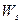 - - 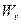 = =  - изменение свободной поверхностной энергии одной молекулы, а - изменение свободной поверхностной энергии одной молекулы, а  - число молекул единицы поверхности жидкости. Тогда - число молекул единицы поверхности жидкости. Тогда 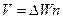 (2). Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, свободная поверхность жидкости стремится сократить свою величину (капля жидкости всегда стремится принять форму шара, обладающего наименьшей поверхностью по сравнению с другими поверхностями). Это объясняется тем, что между молекулами поверхностного слоя, как показывает опыт, действуют силы поверхностного натяжения, направленные по касательной к поверхности перпендикулярно к любой линии на поверхности жидкости. (2). Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, свободная поверхность жидкости стремится сократить свою величину (капля жидкости всегда стремится принять форму шара, обладающего наименьшей поверхностью по сравнению с другими поверхностями). Это объясняется тем, что между молекулами поверхностного слоя, как показывает опыт, действуют силы поверхностного натяжения, направленные по касательной к поверхности перпендикулярно к любой линии на поверхности жидкости.
Можно предположить, что молекулы поверхностного слоя расположены на расстояниях, несколько больших 2rm (рис.1). Эти расстояния уменьшаются по мере удаления от поверхности, и становится несколько меньше 2rm на глубине 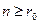 (рис.3). (рис.3).
Силы поверхностного натяжения – это силы взаимного притяжения молекул. Работу увеличения поверхности можно подсчитать, например, при увеличении мыльной пленки (рис.4).
 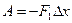
где  - внешняя сила, равна силе поверхностного натяжения, действующая на всю границу поверхности 2 - внешняя сила, равна силе поверхностного натяжения, действующая на всю границу поверхности 2  , но противоположна по направлению: , но противоположна по направлению: 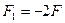
Здесь  - сила поверхностного натяжения, действующего на границу - сила поверхностного натяжения, действующего на границу  , но у пленки две поверхности. Получаем: , но у пленки две поверхности. Получаем: 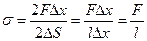
И так, коэффициент поверхностного натяжения измеряется силой поверхностного натяжения, действующей по касательной к поверхности на единицу длины произвольного контура по поверхности жидкости. Не трудно видеть, что это определение соответствует приведенному выше. Размерности коэффициентов, определенные этими двумя путями, совпадают
 =[Дж/м2 ]=[ Н/м] =[Дж/м2 ]=[ Н/м]
Коэффициент поверхностного натяжения зависти от рода жидкости, т.е. от соотношения свободной поверхностной энергии молекул и энергии на глубине жидкости, а также от плотности жидкости, т.к. от нее зависит число молекул единицы поверхности. При нагревании жидкости уменьшается как  , так и , так и 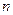 поэтому коэффициент поверхностного натяжения поэтому коэффициент поверхностного натяжения 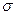 так же уменьшается. Рассмотрим взаимодействие молекул из верхней части сферы молекулярного действия. По мере роста температуры растет плотность пара над поверхностью, а плотность жидкости уменьшается. Поэтому и равнодействующая сил молекулярного притяжения, действующая на каждую молекулу поверхности слоя, уменьшается. так же уменьшается. Рассмотрим взаимодействие молекул из верхней части сферы молекулярного действия. По мере роста температуры растет плотность пара над поверхностью, а плотность жидкости уменьшается. Поэтому и равнодействующая сил молекулярного притяжения, действующая на каждую молекулу поверхности слоя, уменьшается.
Эту температурную зависимость поверхностного натяжения жидкости можно проиллюстрировать на примере воды:
Дата добавления: 2014-09-29 | Просмотры: 1254 | Нарушение авторских прав
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 |
|

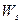 -
- 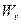 =
=  - изменение свободной поверхностной энергии одной молекулы, а
- изменение свободной поверхностной энергии одной молекулы, а  - число молекул единицы поверхности жидкости. Тогда
- число молекул единицы поверхности жидкости. Тогда 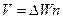 (2). Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, свободная поверхность жидкости стремится сократить свою величину (капля жидкости всегда стремится принять форму шара, обладающего наименьшей поверхностью по сравнению с другими поверхностями). Это объясняется тем, что между молекулами поверхностного слоя, как показывает опыт, действуют силы поверхностного натяжения, направленные по касательной к поверхности перпендикулярно к любой линии на поверхности жидкости.
(2). Поскольку всякая система стремится перейти в состояние с минимальной потенциальной энергией, свободная поверхность жидкости стремится сократить свою величину (капля жидкости всегда стремится принять форму шара, обладающего наименьшей поверхностью по сравнению с другими поверхностями). Это объясняется тем, что между молекулами поверхностного слоя, как показывает опыт, действуют силы поверхностного натяжения, направленные по касательной к поверхности перпендикулярно к любой линии на поверхности жидкости.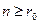 (рис.3).
(рис.3).
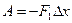
 - внешняя сила, равна силе поверхностного натяжения, действующая на всю границу поверхности 2
- внешняя сила, равна силе поверхностного натяжения, действующая на всю границу поверхности 2  , но противоположна по направлению:
, но противоположна по направлению: 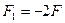
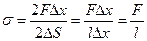
 =[Дж/м2 ]=[ Н/м]
=[Дж/м2 ]=[ Н/м] , так и
, так и 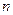 поэтому коэффициент поверхностного натяжения
поэтому коэффициент поверхностного натяжения 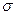 так же уменьшается. Рассмотрим взаимодействие молекул из верхней части сферы молекулярного действия. По мере роста температуры растет плотность пара над поверхностью, а плотность жидкости уменьшается. Поэтому и равнодействующая сил молекулярного притяжения, действующая на каждую молекулу поверхности слоя, уменьшается.
так же уменьшается. Рассмотрим взаимодействие молекул из верхней части сферы молекулярного действия. По мере роста температуры растет плотность пара над поверхностью, а плотность жидкости уменьшается. Поэтому и равнодействующая сил молекулярного притяжения, действующая на каждую молекулу поверхности слоя, уменьшается.