|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
МУЛЬТИПОЛЬНЫЙ ЭКВИВАЛЕНТНЫЙ ГЕНЕРАТОР
В электрическом отношении сердце можно рассматривать как совокупность электрических зарядов (ионов), распределенных некоторым определенным образом в области сердца. Электрические поля отдельных ионов, накладываясь друг на друга, создают в любой точке пространства результирующее поле, потенциал которого равен сумме потенциалов полей, создаваемых этими зарядами (принцип суперпозиции полей). Вычислить такую сумму практически невозможно, так как точное распределение зарядов в области сердца (и его изменения с течением времени) не известно. Однако, из электродинамики известно, что если заряды распределены в некоторой области пространства, то потенциал поля, создаваемого этими зарядами в удаленной от них точке, можно представить в виде, следующей бесконечной суммы:
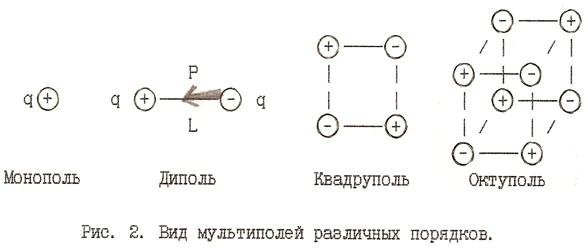
где r - расстояние от системы зарядов до точки с потенциалом φ; f1, f2,f3….- некоторые функции, зависящие от вида зарядов, от свойств среды и от направления на интересующую нас точку (конкретный вид функций f1 и f2 будет рассмотрен ниже). Первое слагаемое в формуле (1) соответствует потенциалу, создаваемому монополем, второе - диполем, третье - квадруполем и т. д. Общее название подобных распределений зарядов - электрические мультиполи. Мультиполи бывают различных порядков К (К =0,1,2,3…) Число зарядов мультиполя определяется выражением 2к. На значительных расстояниях r от мультиполя (r >>L, где L – размеры мультиполя) потенциал его поля убывает пропорционально Монополь или мультиполь нулевого порядка (20=1)- это просто точечный заряд g. На расстоянии r потенциал поля (первое слагаемое в формуле 1). Диполь – это мультиполь первого порядка (21= 2). Электрическим диполем называют систему, состоящую из двух равных по величине, но противоположных по знаку точечных зарядов, расположенных друг от друга на расстоянии L (плечо диполя). Основной характеристикой диполя является его электрический дипольный момент(Р), равный произведению заряда g на плечо диполя L. Р = g*L (2) Дипольный момент Р – это вектор. Он направлен от отрицательного заряда к положительному. В точке, удаленной от диполя на расстояние r, потенциал его поля Квадруполь – мультиполь второго порядка (22=4). Он может быть представлен системой из 4 зарядов. На расстоянии r потенциал поля, coздаваемого квадруполем, Октуполь – это мультиполь третьего порядка (23= 8). Он состоит из 8 зарядов, а потенциал его поля определяется выражением
Физико –математическая модель, описывающая потенциал электрического поля сердца уравнением (1) называется мультипольным эквивалентным электрическим генератором сердца. В зависимости от степени точности, с которой мы хотим определить потенциал поля, могут использоваться различные виды мультипольных эквивалентных генераторов, содержащие разное число слагаемых из уравнения (1). Определим, какие слагаемые уравнения (1) являются наиболее важными. В организме все ионы образуются при диссоциации нейтральных молекул и поэтому в миокарде числа отрицательных и положительных ионов одинаковы, а их суммарный заряд равен нулю. Это значит, что первое слагаемое в уравнении (1) равно нулю, так как именно оно зависит от общего заряда системы. Мультиполи высоких порядков мало влияют на потенциал достаточно удаленных точек, так как их вклaд обратно пропорционален высоким степеням расстояния до точки (1/rk+1)). Таким образом, потенциал поля сердца определяется главным образом его дипольным моментом. Модель, в которой электрическая активность миокарда заменяется действием одного эквивалентного точечного диполя, называется дипольным эквивалентным генератором сердца. Это понятие лежит в основе теории Эйнтховена и будет в дальнейшем рассмотрено нами более подробно. Следует отметить, что расстояния до точек, в которых на поверхности. тела регистрируются биопотенциалы, все-таки не очень велики по сравнению с размерами самого сердца. Поэтому для более точного моделирования сердечной деятельности применяют эквивалентные генераторы, учитывающие квадрупольный член или рассматривают сердце как совокупность нескольких диполей, легализованных в разных его участках – многодипольные эквивалентные генераторы. Например, модели Миллеоа и Гезелоувитца, Баума и Дубровина и другие (5) Дата добавления: 2014-09-29 | Просмотры: 2251 | Нарушение авторских прав |
 (1)
(1) .
.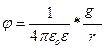
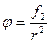 (второе слагаемое в формуле 1).
(второе слагаемое в формуле 1).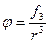 (третье слагаемое в формуле 1)
(третье слагаемое в формуле 1) (четвертое слагаемое в формуле 1)
(четвертое слагаемое в формуле 1)