 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
По методу отрыва капельОписание капельного метода. Метод отрыва капель, не будучи очень точным, является, однако, употребляемым в медицинской практике. Теоретическое обоснование метода заключается в следующем: образование капель жидкости при ее вытекании из отверстия является результатом взаимодействия силы поверхностного натяжения и силы тяжести. Перед отрывом капли у конца трубки образуются перетяжка (а,в) по которой происходит отрыв. Длина контура по которому происходит отрыв, т.е. разрывается поверхностная пленка капли равна длине окружности перетяжки. Силы поверхностного натяжения по контуру будет равна
Перед самым отрывом эта сила уравновешивает вес капли: Если известны Р и
в место радиуса перетяжки радиус трубки нельзя, (Рис.5) т.к. радиус трубки больше радиуса перетяжки. Чтобы избежать измерения радиуса перетяжки берут две жидкости, одну эталонную, коэффициент поверхностного натяжения известен, другую исследуемую. Тогда можно записать два уравнения: Для исследуемой жидкости Для эталонной жидкости Где Р1 – вес капли исследуемой жидкости, Р2 – вес капли воды Деля почленно (3) на (4) получим Для нахождения веса одной капли поступают следующим образом: отсчитывают число капель исследуемой жидкости и воды вытекающей из одного и того же объема. При этом скорость вытекания капли должна быть одинакова, только при этом условии можно считать, что радиусы перетяжек будут равны. Пусть Для исследуемой жидкости.
для воды где
Отсюда получим: Таким образом, для определения коэффициента поверхностного натяжения нужно знать число капель n1 и n2 исследуемой и эталонной жидкости, плотности этих жидкостей и значение коэффициента поверхности натяжения Дата добавления: 2014-09-29 | Просмотры: 2217 | Нарушение авторских прав |
 (1), где
(1), где 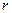 - радиус перетяжки.
- радиус перетяжки.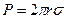
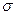 находится из выражения:
находится из выражения: (2)
(2) Вес капли может быть легко определен, но определение радиуса перетяжки весьма затруднительно. Представлять же
Вес капли может быть легко определен, но определение радиуса перетяжки весьма затруднительно. Представлять же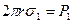 (3)
(3) (4)
(4)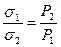
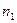 число капель исследуемой жидкости, а
число капель исследуемой жидкости, а  число капель эталонной жидкости во взятом объеме V, а D1 D2 соответствующие плотности этих жидкостей. Тогда вес одной капли в каждой жидкости выразится соотношением:
число капель эталонной жидкости во взятом объеме V, а D1 D2 соответствующие плотности этих жидкостей. Тогда вес одной капли в каждой жидкости выразится соотношением: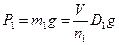 (5)
(5) (6)
(6)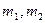 - масса капель, V – объем одной капли,
- масса капель, V – объем одной капли, - ускорение силы тяжести
- ускорение силы тяжести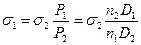
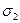 эталонной жидкости.
эталонной жидкости.