 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
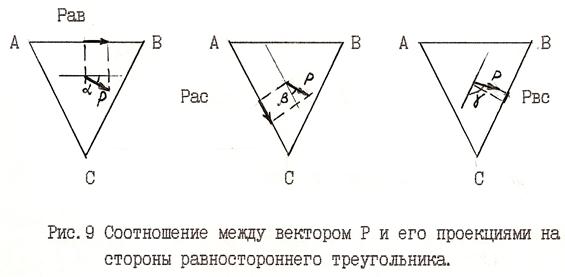
Соотношения между проекциями момента диполя и напряжениемЛюбой вектор полностью характеризуются его проекциями на две координатные оси, лежащие в той же плоскости, что и сам вектор. Наиболее привычной для нас является декартова система координат с двумя взаимно перпендикулярными осями, хотя использование любых других (непараллельных) осей тоже возможно. Как будет показано в разделах 6.4 и 6.5 наиболее удобными в данном случае оказываются оси, расположенные по сторонам равностороннего треугольника.
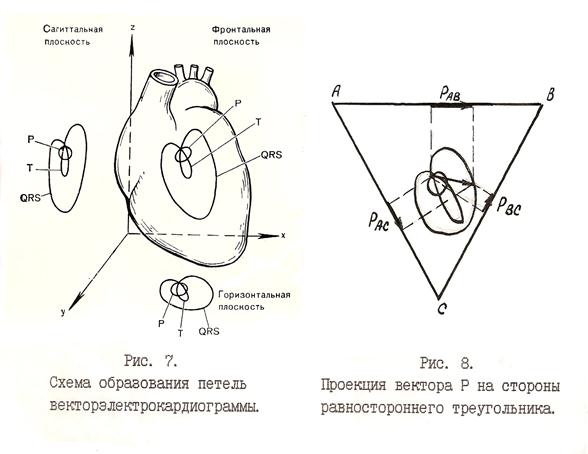
Если точечный диполь, создающий электрическое поле, находится в центре равностороннего треугольника АВС, то из формулы (7) следует, что напряжения на концах сторон этого треугольника относятся как проекции вектора Р на его стороны (рис. 8), так как зависимости от расстояния (r) и от угла (ß) в формуле (7) будут одинаковыми и при вычислении отношения сократятся: UАВ:U ВС :UАС=РАВ:РВС:РАС (8) Из соотношения (8), измерив напряжения UАВ, UВС, UАС, можно определить относительную величину проекций вектора Р на стороны треугольника: РАВ, РВС, РАС, а по известным проекциям, в свою очередь, можно рассчитать величину самого вектора Р (рис. 9).
Таким образом, соотношение между электрическим вектором
сердца и потенциалами точек на поверхности тела человека наиболее просто устанавливается в том случае, еслиэти потенциалы измерены в точках, расположенных в вершинах равностороннего треугольника по отношению к ЭВС.
Дата добавления: 2014-09-29 | Просмотры: 995 | Нарушение авторских прав |
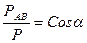, РАВ=РСosα