АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология

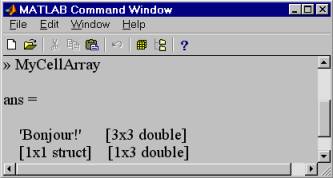
Fieldnames( s ) - возвращает массив строк с именами всех полей

Структуры MATLABа можно назвать агрегированным типом данных. Другим агрегированным типом данных в системе MATLAB являются так называемые ячейки (cells).

#$+Массивы ячеек.

Массив ячеек может содержать в качестве элементов массивы разных типов! Таким образом, он является универсальным контейнером - его ячейки могут содержать любые типы и структуры данных, с которыми работает MATLAB - массивы чисел любой размерности, строки, массивы структур и другие (вложенные) массивы ячеек. Массив ячеек может быть полем структуры.

Методы создания массивов ячеек похожи на методы создания структур. Как и в случае структур, массивы ячеек могут быть созданы либо путём последовательного присваивания значений отдельным элементам массива, либо созданы целиком при помощи специальной функции cell(). Однако в любом случае важно различать ячейку (элемент массива ячеек) и её содержимое. Ячейка - это содержимое плюс некоторая оболочка (служебная структура данных) вокруг этого содержимого, позволяющая хранить в ячейке произвольные типы данных любого размера.

Выражение любого типа данных системы MATLAB можно превратить в ячейку, заключив его в фигурные скобки. Тогда с помощью следующих присваиваний и обычных операций индексации

MyStruct = struct('field1',[ 1 2 3],'field2','Hello');

MyCellArray(1, 1) = { 'Bonjour!' };

MyCellArray(1, 2) = { [ 1 2 3; 4 5 6; 7 8 9 ] };

MyCellArray(2, 1) = { MyStruct };

MyCellArray(2, 2) = { [ 9 7 5 ] };

строится массив ячеек 2x2, элементами которого являются ячейки, содержащие соответственно текстовую строку, числовой массив 3x3, структуру MyStruct и вектор-строку 1x3. Итак, построенный массив ячеек содержит разнородные данные, о чём нам и сообщает система MATLAB при вводе имени такого массива и нажатии клавиши Enter:

При этом показывается содержимое не всех ячеек этого массива. Более подробную информацию можно получить, вызвав функцию celldisp(MyCellArray):

MyCellArray{1,1} =

Bonjour!

MyCellArray{2,1} =

field1: [ 1 2 3 ]

field2: 'Hello'

MyCellArray{1,2} =

1 2 3

4 5 6

7 8 9

MyCellArray{2,2} =

9 7 5

Отсюда видно, что для того, чтобы подобраться к содержимому ячеек, нужно индексировать массив ячеек при помощи фигурных скобок. При обычной индексации круглыми скобками мы из массива ячеек извлекаем отдельную ячейку. Напоминаем ещё раз о том, что следует чётко различать саму ячейку и её содержимое (см. выше).

Массивы ячеек полностью решают типовую задачу хранения нескольких строковых данных под одним именем. Раньше мы уже формировали матрицы типа char, каждая строка которых имела одну и ту же длину. Это очевидным образом ограничивает применение такого решения. В случае массива ячеек такого ограничения нет:

cellNames{ 1 } = 'function1';

cellNames{ 2 } = 'func2';

Здесь мы продемонстрировали применение фигурных скобок в роли индексирующих элементов, так что использовать фигурные скобки в правых частях операции присваивания теперь не нужно (там присутствуют значения, а не ячейки). В итоге под именем массива cellNames хранятся две текстовые строки (можно и больше), доступ к каждой из которых осуществляется по индексу в соответствии с синтаксисом массива ячеек. Вот код, который выводит на экран обе текстовые строки:

disp(cellNames{ 1 }); disp(cellNames{ 2 });

Как и в случае структур, показанное выше поэлементное создание массива ячеек неэффективно с точки зрения производительности. Это не создаёт проблем в медленном интерактивном режиме работы, но в программном режиме этот процесс лучше предварить вызовом функции cell():

MyCellArray = cell(2, 2);

которая сразу создаст массив ячеек требуемой размерности и размера, причём каждая ячейка будет пустой. Пустые ячейки обозначаются как {[]}. Затем можно осуществлять ранее рассмотренные поэлементные присваивания, так как теперь они не требуют перестройки структуры массива с каждым новым присваиванием.

Содержимым пустой ячейки является пустой числовой массив, который, как мы знаем, обозначается []. Чтобы удалить некоторый диапазон ячеек из массива ячеек, нужно этому диапазону присвоить значение пустого массива []:

MyCellArray(2,:) = [];

Теперь массив ячеек MyCellArray имеет размер 1x2, так как мы только что удалили всю вторую строку массива.

У массивов ячеек имеется множество полезных применений. Например, с помощью массива ячеек решается задача организации M-функции, которой можно передать произвольно большое число аргументов. Допустим, требуется вычислить суммарную длину заранее неизвестного числа вектор-строк. Эта задача решается с помощью ключевых слов varargin и varargout (второе ключевое слово используется, когда M-функция возвращает заранее неизвестное число выходных значений).

В определении M-функции параметр, через который передаётся заранее неизвестное число входных аргументов, нужно обозначить ключевым словом varargin. Им обозначается массив ячеек, в который упакованы эти параметры. Функция всегда может узнать истинное число аргументов в этом параметре, вычислив функцию length. Ниже представлен код функции, вычисляющей сумму квадратов длин вектор-строк:

function sumlen = NumLength(varargin)

n= length(varargin);

sumlen = 0;

for k = 1: n sumlen = sumlen + varargin{ k }(1)^2 +varargin{ k }(2)^2;

End

Если аргумент varargin не единственный в списке параметров, то он должен стоять последним. В рассмотренном примере с помощью фигурных скобок мы извлекаем содержимое отдельной ячейки, то есть вектор, а с помощью дальнейшей индексации круглыми скобками извлекаем первую и вторую координаты вектора.

При вызове функции NumLength не нужно (и нельзя) упаковывать входные числовые вектор-строки в массив ячеек, так как MATLAB делает это сам. Достаточно перечислить их в качестве фактических параметров через запятую:

NumLength([ 1 2], [3 4])

ans =

Теперь вызовем функцию NumLength с другим числом параметров:

NumLength([ 1 2], [3 4], [ 5 6])

ans =

Функция легко обрабатывает оба этих случая.

Использование массивов ячеек для передачи M-функциям произвольного числа параметров (или для возвращения функцией произвольного числа выходных значений) является единственно возвожным решением проблемы. Существуют ещё и другие случаи, когда обязательно требуется применение массива ячеек. О них будет рассказано в следующей главе. А сейчас ещё упомянем удобный способ заменить список величин, разделённых запятыми, компактным индексным выражением с массивом ячеек.

Таким заменителем является индексное выражение, извлекающее содержимое диапазона ячеек из массива ячеек. Для примера рассмотрим функцию plot(), которая изучалась нами в главе, посвящённой построению графиков функций. Этой функции в качестве параметров передаются массив значений независимой переменной, массив значений зависимой переменной и текстовая строка, управляющая внешним видом графика. Для компактности все эти переменные (массивы) можно упаковать в массив ячеек, например,

F(1) = { 0: 0.1: pi };

F(2) = { sin(F{1}) };

F(3) = { 'bo:' };

Теперь вся информация, необходимая для построения графика функции сосредоточена в единственной переменной F. Построение графика функции можно осуществить с помощью компактного выражения

plot(F{ 1: 3 })

так как операция взятия содержимого диапазона ячеек с точки зрения системы MATLAB порождает список величин, разделённых запятыми.

#$+Чтение и запись файлов данных.

Ранее были рассмотрены MAT-файлы, в которых сохраняются переменные из рабочей области системы MATLAB. Также были рассмотрены M-файлы, хранящие текст M-функций. Теперь рассмотрим файлы произвольного формата, в которых M-функции могут записывать, а затем читать собственные данные.

Под собственными данными мы последовательно рассмотрим запись содержимого числовых векторов и матриц, текстовых строк, структур и массивов ячеек.

Начнём с числовых векторов и матриц. Работать будем с так называемыми бинарными (не текстовыми) файлами, которые сначала надо открыть с помощью предназначенной для этого функцией fopen системы MATLAB:

fid = fopen('имя-файла', 'флаг')

где имя файла может предваряться полным путём к нему (иначе файл должен располагаться в текущем каталоге MATLABа). Второй параметр этой функции - так называемый флаг открытия файла, говорит о способе дальнейшей работы с файлом:

'rb' - только для чтения

'wb' - только для записи (предыдущее содержимое теряется)

Вторая буква в этих примерах говорит о бинарном характере файлов. Возможен ещё флаг, разрешающий как чтение, так и запись файлов одновременно ('r+'), но мы его здесь использовать не будем.

Функция fopen возвращает числовой идентификатор открытого файла, который надо использовать в качестве параметра для функций чтения и записи в этот файл. Если операция открытия файла не удалась (это возможно как по причине отсутствия файла, так и по причине неправильного указания пути к нему на диске), то функция fopen возвращает -1.

Всегда следует проверять возврат функции fopen:

fid = fopen('имя_файла', 'флаг');

if(fid == -1)

Дата добавления: 2015-01-18 | Просмотры: 818 | Нарушение авторских прав