|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Global hAxes hEd1 hEd2 hEd3 hEd4 hList
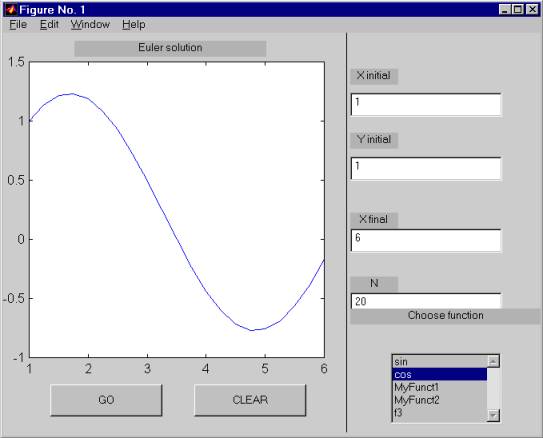
%-- get string information from editboxes ----- str1=get(hEd1,'String'); str2=get(hEd2,'String'); str3=get(hEd3,'String'); str4=get(hEd4,'String'); %-- convert strings to numbers --------------- x0 = str2num(str1); y0 = str2num(str2); xf = str2num(str3); N = str2num(str4); %-- get function name ------------------------- index = get(hList, 'Value'); cellArr = get(hList, 'String'); funName = cellArr{ index }; %-- Euler algorithm --------------------------- axes(hAxes); dx = (xf - x0) / N; X=x0; Y=y0; for k=1:N Y=[ Y, Y(end) + feval(funName, X(end)) * dx ]; X=[ X, X(end) + dx ]; End %-- graph plotting --------------------------- plot(X, Y); С помощью функций get, указывая им в качестве первого аргумента описатели редактирующих полей, мы получаем значения свойства 'String', то есть текстовое содержимое этих полей, которое вводится пользователем с клавиатуры. Это и есть входные данные. Только пока что числовые данные представлены в строковой (текстовой) форме. Для получения имени функции, представляющей правую часть дифференциального уравнения, сначала у списка запрашиваем через свойство 'Value' индекс подсвеченной (выбранной или отселектированной) строки, затем читаем значение свойства 'String'. Последнее для списка является массивом ячеек, откуда и выбираем имя функции с помощью операции индексирования массива ячеек. С помощью функций str2num преобразуем текстовые величины в числа. Затем устанавливаем начальные значения для массива X значений аргумента и массива Y значений функции на сетке. Шаг сетки (шаг интегрирования) dx вычисляется делением длины отрезка интегрирования на количество шагов N, которое пользователь вводит с клавиатуры. Наращивание массивов осуществляется операцией конкатенации, в то время как очередное значение функции вычисляется согласно алгоритму метода Эйлера и равно feval(funName, X(end)) * dx Ключевое слово системы MATLAB end означает ссылку на последний элемент массива, что нам и требуется в данном случае. С помощью функции feval осуществляется вызов функции с именем funName, прочитанным из списка, и ей передаётся аргумент X(end)(текущее значение независимого аргумента). В конце концов осуществляется построение графика вычисленного решения дифференциального уравнения с помощью функции plot. Перед вызовом этой функции с помощью axes(hAxes) гарантируется, что наш объект типа Axes является активным, и именно в нём функция plot строит график функции. Проверим работу приложения для следующих пользовательских функций MyFunct1, MyFunct2 и f3. Текст функции MyFunct1 function ret = MyFunct1(x) ret = x ^ 3; записываем в файл MyFunct1.m. Текст функции MyFunct2 function ret = MyFunct2(x) ret = 1 / sin(x); записываем в файл MyFunct2.m. Наконец, текст функции f3 function ret = f3(x) ret = sin(x * x); записываем в файл f3.m. Начинаем с простой функции cos(x):
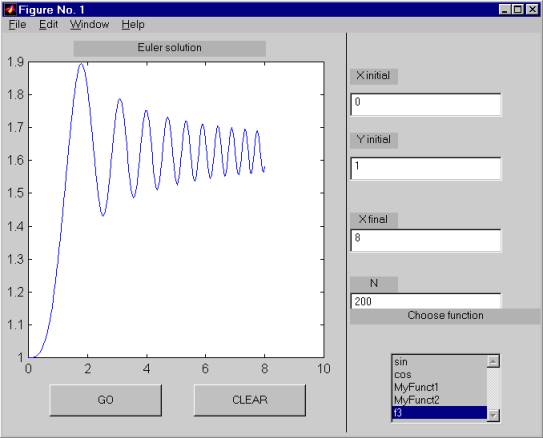
Так как дифференциальное уравнение y'(x)=cos(x) имеет аналитическое решение y(x) = Yinitial - sin(Xinitial) + sin(x) то в полученном графике легко узнать график функции sin(x), сдвинутый вдоль вертикальной оси вверх. Также очевидые решения получаются для функций sin и MyFunct1, так как и в этих случаях существуют тривиальные аналитические решения. В случае выбора функции MyFunct2 аналитическое решение существует в виде довольно замысловатой функции Yinitial + ln(| tg(x / 2) / tg(Xinitial / 2) |) а в случае функции f3 аналитического решения не существует, и единственным способом остаются непосредственные численные расчёты. Следующий рисунок иллюстрирует решение дифференциального уравнения y'(x) = f3(x), где функция f3(x)=sin(x^2):
Созданное нами законченное приложение в рамках среды MATLAB удобно применять также для иллюстрации процесса сходимости приближённого решения к точному по мере увеличения числа шагов интегрирования N (то есть уменьшения шага интегрирования). Заметим, что создание графических окон с элементами управления возможно не только с помощью "ручного" написания соответствующих M-файлов, изобилующих вызовами функций -конструкторов типа uicontrol, Axes и так далее. Этот способ, который мы рассмотрели подробно, является наилучшим с точки зрения максимального контроля разработчика над процессом разработки. В случае недостаточной квалификации разработчика (или необходимости очень быстрого выполнения работы) ему на помощь может прийти специальное визуальное средство разработки, входящее в пакет MATLAB - так называемый guide. По этой команде на экран дисплея выводится специальное окно, содержащее палитру графических элементов управления. С помощью мыши можно методом буксировки "перетаскивать" эти элементы на создаваемое собственное графическое окно. Правда callback-функции все равно нужно писать отдельно и самостоятельно. Изучение средства guide удобно проводить под руководством преподавателя на практическом занятии, повторяя демонстрируемые действия. #$Глава 5. Дата добавления: 2015-01-18 | Просмотры: 740 | Нарушение авторских прав |