 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Приравнивая правые части этих выражений, получим
Это каноническое уравнение прямой на плоскости. Частные случаи этого уравнения уже обсуждались, когда рассматривали параметрические уравнения прямой. Когда q 1 = 0, q 2 ≠ 0, q (0, q 2), тогда уравнение x = x 0 можно рассматривать и как каноническое уравнение. В случае q 1 ≠ 0, q 2 = 0, q (q 1, 0), получаем y = y 0.
5. уравнение прямой, проходящей через две заданные точки Пусть даны точки А (xA, yA) и В (xB, yB). Запишем каноническое уравнение. В качестве направляющего вектора прямой (АВ) можно взять вектор
Полученное уравнение называется уравнением прямой, проходящей через две заданные точки. Очевидно, что если xA = xB = C (C = const), то А (С, yA), В (С, yB) и уравнение прямой будет иметь вид: x = C (рис. 25). Если yA = yB = C, то уравнение будет: y = C (рис. 26).
6. нормальное уравнение прямой Рассмотрим общее уравнение прямой на плоскости: Ax + By + C = 0, очевидно, что получим уравнение
Знак перед корнем выбираем противоположный знаку С. Учитывая, что (А, В) – координаты нормального вектора n, то деление на
тогда модуль
Пусть φ – угол между вектором единичной длины n 0 и положительным направлением оси Оx (рис. 27), тогда
Учитывая, что величина x cosφ + y sinφ – p = 0. Геометрический смысл угла φ ясен – это угол между вектором n 0 и положительным направлением оси Оx, выясним смысл параметра p. Найдем расстояние от прямой x cosφ + y sinφ – p = 0 до начала координат (рис. 28). Для этого запишем уравнение прямой, проходящей через начало координат, перпендикулярно данной. Очевидно, что в качестве направляющего вектора можно взять вектор n 0(cosφ, sinφ), вместо начальной точки точку О (0, 0). Воспользовавшись каноническим уравнением, получим
Решая систему
найдем точку пересечение этих прямых. Из первого уравнения имеем
подставляем во второе уравнение
=> Решение системы:
Cледовательно, (p cosφ, p sinφ) – точка пересечения прямых. Найдем расстояние от точки пересечения до начала координат, получим
Таким образом, р – это расстояние от прямой x cosφ + y sinφ – p = 0 до начала координат. Уравнение x cosφ + y sinφ – p = 0 называют нормальным уравнением прямой. 7. уравнение прямой с угловым коэффициентом Рассмотрим общее уравнение прямой Ax + By + C = 0, предположим, что B ≠ 0, тогда By = – Ax – C => Обозначим y = kx + b, называемое уравнением прямой с угловым коэффициентом. Смысл параметра b был выяснен ранее – это длина отрезка, отсекаемого прямой на оси ординат. При этом b > 0, если отсекается отрезок в положительной части оси Oy, и b < 0, если отрезок отсекается в отрицательной части оси Oy. Как известно из школьного курса математики, k – это тангенс угла наклона, образованный прямой и положительной частью оси Ox (угол считается от оси Ox против часовой стрелки). Если k > 0, то угол острый, при k < 0 угол тупой (рис. 29, 30).
Уравнение прямой с угловым коэффициентом можно получить и из канонического уравнения. Пусть прямая задана уравнением
Тогда, выражая y, получаем q 2(x – x 0) = q 1(y – y 0) => => Обозначим y = kx + b.
8. примеры решения типовых задач
Пример1. Дано: n (3, 2) – нормальный вектор, точка M 0(–2, 6) – начальная точка (рис. 31). Запишем уравнение прямой, проходящей через точку М 0, перпендикулярно вектору n. Пусть точка М (x, y) лежит на прямой, тогда вектор (n, 3(x + 2) + 2(y – 6) = 0, 3 x + 6 + 2 y – 12 = 0, 3 x + 2 y – 6 = 0. Это общее уравнение прямой.
3 x + 2 y = 6. Разделим уравнение на 6:
Из уравнения в отрезках видно, что отрезки, отсекаемые на осях Ox и Oy, соответственно равны a = 2, b = 3 (рис. 32). Выразим из общего уравнения 3 x + 2 y – 6 = 0 переменную y, получим 2y = –3x + 6 => Это уравнение прямой с угловым коэффициентом, где k = –3/2 < 0, угол α – тупой, b = 3.
(n, q) = 0 => 3 ∙ (–2) + 2 ∙ 3 = 0, следовательно, q параллелен прямой (рис. 33). Запишем каноническое уравнение прямой:
с начальной точкой М 0(–2, 6) и направляющим вектором q (–2, 3). Приравняем полученные дроби параметру t, получим
Выражаем переменные x и y:
получаем уравнения:
Это параметрические уравнения прямой. Заметим, что точки М 0(–2, 6) и М 1(4, –3) лежат на прямой. Запишем уравнение прямой, проходящей через две заданные точки:
Преобразовав это уравнение, получим: –9 x – 18 = 6 y – 36 => 3 x + 2 y – 6 = 0. Мы получили первоначальное общее уравнение. Разделим общее уравнение на
Это нормальное уравнение прямой, где Пример 2. Даны вершины треугольника А (1, 1), В (10, 13), С (13, 6). Составить уравнения медианы, высоты и биссектрисы угла А. Медиана – прямая, проходящая через точку А и середину противоположной стороны ВС. Найдем середину стороны ВС и обозначим ее А ′:
Получаем А ′(11,5; 9,5). Запишем уравнение прямой, проходящей через две точки А и А ′:
Преобразовывая это уравнение, получим: 8,5 x – 8,5 = 10,5 y – 10,5 => 8,5 x – 10,5 y + 2 = 0 => => 17 x – 21 y + 4 = 0. Это общее уравнение медианы АА ′. Высота – прямая, проходящая через точку А, перпендикулярно прямой ВС. Запишем уравнение прямой ВС:
Воспользовавшись свойством пропорции, преобразуем уравнение: –7 x + 70 = 3 y – 39 => 7 x + 3 y – 109 = 0. Это общее уравнение прямой ВС. Записать уравнение прямой, перпендикулярной данной, можно разными способами. Например, можно записать каноническое уравнение прямой, проходящей через точку А (1; 1) с направляющим вектором q (7; 3). (В данном случае вектор нормали n прямой ВС можно рассматривать как направляющий вектор высоты). Каноническое уравнение высоты будет иметь вид:
Перейдем к общему уравнению: 3 x – 3 = 7 y – 7 => 3 x – 7 y + 4 = 0. Можно было бы получить уравнение высоты, используя уравнение с угловым коэффициентом. Две прямые, заданные уравнениями y = k 1 x + b 1 и y = k 2 x + b 2 перпендикулярны, если k 1 ∙ k 2 = –1. Запишем уравнение прямой ВС с угловым коэффициентом: 7 x + 3 y – 109 = 0 => 3 y = –7 x + 109 => k 1 = –7/3, значит, k 2 = 3/7. Тогда уравнение прямой, перпендикулярной ВС, будет иметь вид
Значение параметра b найдем, подставив в уравнение координаты точки А (1; 1):
И уравнение приобретет вид Найдем уравнение биссектрисы. Пусть D – точка пересечения биссектрисы со стороной ВС. Из свойства биссектрисы внутреннего угла треугольника следует, что | BD |: | DC | = | AB |: | AC |. Найдем длины сторон треугольника:
Следовательно, точка D делит отрезок ВС в отношении
Остается записать уравнение прямой, проходящей через две точки А (1; 1) и
Воспользовавшись свойством пропорции, получаем 231 x – 231 = 297 y – 297 => 231 x – 297 y + 66 = 0. Разделим уравнение на 33, получим 7 x – 9 y + 2 = 0. Это общее уравнение биссектрисы. Эту задачу можно было решить, используя формулу для нахождения расстояния d от точки М (x 1; y 1) до прямой Ax + By + C = 0:
Биссектрису угла можно рассматривать как прямую, каждая точка которой равноудалена от сторон угла. Найдем уравнение сторон АВ и АС. Для стороны АВ имеем:
Разделим уравнение на 3 и приведем подобные слагаемые: 4 x – 3 y – 1 = 0. Это уравнение прямой АВ. Для стороны АС аналогично получаем:
=> 5 x – 12 y + 7 = 0. Это уравнение прямой АС. Расстояние от произвольной точки М (x; y) до прямой АВ:
Расстояние от М до прямой АС:
Учитывая, что dAB = dAC, получаем
=> 52 x – 39 y – 13 = ± (25 x – 60 y + 35). Одна прямая имеет вид 52 x – 39 y – 13 = 25 x – 60 y + 35 => 27 x + 21 y – 48 = 0 => => 9 x + 7 y – 16 = 0. Другая прямая: 52 x – 39 y – 13 = –25 x + 60 y – 35 => 77 x – 99 y + 22 = 0 => => 7 x – 9 y + 2 = 0. Мы получили два уравнения биссектрис внешнего и внутреннего углов. Найдем их точки пересечения с прямой ВС, ее уравнение было получено выше: 7 x + 3 y – 109 = 0. Решаем систему:
Получаем y = –39,5, x = 32,5. Точка с координатами (32,5; –39,5) не лежит на отрезке ВС, где В (10; 13) и С (13; 6). Следовательно, 9 x + 7 y – 16 = 0 уравнение биссектрисы внешнего угла. Найдем точку пересечение второй биссектрисы со стороной BС:
Как видно, точка с координатами
Дата добавления: 2015-01-18 | Просмотры: 748 | Нарушение авторских прав |
 .
. с координатами (xB – xA, yB – yA). В качестве начальной точки можно выбрать любую из точек А или В. Пусть это будет точка А (xA, yA):
с координатами (xB – xA, yB – yA). В качестве начальной точки можно выбрать любую из точек А или В. Пусть это будет точка А (xA, yA):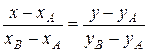 .
.

 . Разделим уравнение на корень
. Разделим уравнение на корень 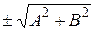 ,
, .
. приводит нормаль к вектору единичной длины, коллинеарному исходному вектору n. Действительно, пусть
приводит нормаль к вектору единичной длины, коллинеарному исходному вектору n. Действительно, пусть ,
,
 .
.
 ,
, .
. всегда отрицательна, обозначим эту дробь (– p), где p > 0, уравнение при этом примет вид:
всегда отрицательна, обозначим эту дробь (– p), где p > 0, уравнение при этом примет вид:
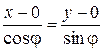 .
.
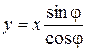 ,
, =>
=>  =>
=> .
.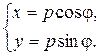
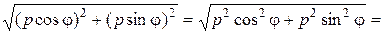
 .
. .
. , для второй дроби было введено обозначение, когда рассматривалась прямая в отрезках,
, для второй дроби было введено обозначение, когда рассматривалась прямая в отрезках,  . Получим привычное со средней школы уравнение
. Получим привычное со средней школы уравнение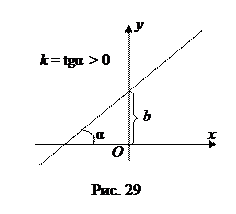

 =>
=>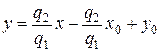 .
. ,
,  , получаем требуемое уравнение
, получаем требуемое уравнение Рассмотрим несколько задач, иллюстрирующих связь и преимущества различных способов задания прямой на плоскости.
Рассмотрим несколько задач, иллюстрирующих связь и преимущества различных способов задания прямой на плоскости. (x + 2, y – 6) перпендикулярен n и, значит, их скалярное произведение равно нулю:
(x + 2, y – 6) перпендикулярен n и, значит, их скалярное произведение равно нулю: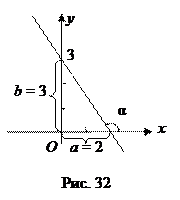 Перейдем к уравнению в отрезках. Для этого перенесем свободный член в правую часть:
Перейдем к уравнению в отрезках. Для этого перенесем свободный член в правую часть: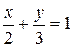 .
. .
. В качестве направляющего вектора прямой можно взять вектор q (–2, 3). Действительно, указанный вектор q (–2, 3) перпендикулярен вектору n (3, 2), т.к. их скалярное произведение равно нулю:
В качестве направляющего вектора прямой можно взять вектор q (–2, 3). Действительно, указанный вектор q (–2, 3) перпендикулярен вектору n (3, 2), т.к. их скалярное произведение равно нулю: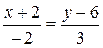
 .
. и
и  ,
, или
или 
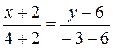 =>
=> 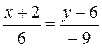 .
. , придем к уравнению
, придем к уравнению .
.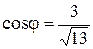 ,
,  и расстояние от начала координат до прямой равно
и расстояние от начала координат до прямой равно  .
.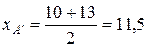 ;
;  .
. =>
=> 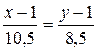 .
. =>
=>  .
. .
. .
. .
.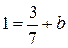 =>
=>  .
. .
.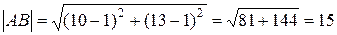 ,
, .
. и, значит, координаты D будут определяться формулами:
и, значит, координаты D будут определяться формулами: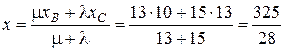 ,
, .
. :
: =>
=>  .
. .
. =>
=> 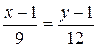 => 12 x – 12 = 9 y – 9.
=> 12 x – 12 = 9 y – 9. =>
=>  => 5 x – 5 = 12 y – 12 =>
=> 5 x – 5 = 12 y – 12 => .
.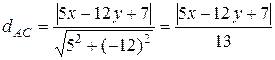 .
. =>
=>  =>
=>

 лежит внутри отрезка ВС. Следовательно, второе уравнение и есть уравнение биссектрисы внутреннего угла А.
лежит внутри отрезка ВС. Следовательно, второе уравнение и есть уравнение биссектрисы внутреннего угла А.