 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Уравнения плоскости1. общее уравнение плоскости Плоскость задается однозначно, если известен вектор, которому она перпендикулярна и точка, через которую она проходит. Аналогично прямой на плоскости, такой вектор называется нормальным вектором или вектором нормали, точка называется начальной точкой, обозначим нормаль n (A, B, C) и начальную точку M 0(x 0, y 0, z 0). Произвольная точка M (x, y, z) лежит на плоскости в том и только том случае, когда вектор
получаем (n, Раскрывая скобки и перегруппировывая слагаемые, имеем: Ax + By + Cz – Ax 0 – By 0 – Cz 0 = 0. Обозначив – Ax 0 – By 0 – Cz 0 через D, придем к уравнению: Ax + By + Cz + D = 0. Это общее уравнение плоскости. Рассмотрим частные случаи. 1) Пусть D = 0, уравнение принимает вид Ax + By + Cz = 0. Очевидно, что в этом случае плоскость проходит через начало координат. 2) Если одна из координат нормального вектора равна нулю, то плоскость параллельна соответствующей оси координат. Например, А = 0, тогда By + Cz + D = 0 – плоскость, параллельная оси Ох, при В = 0 плоскость параллельна оси Оу, при С = 0 – оси Оz. 3) Если две координаты нормального вектора равны нулю, то плоскость перпендикулярна одной из осей координат и параллельна соответствующей координатной плоскости. Например, А = В = 0, тогда Cz + D = 0 или z = – D / C. Это уравнение плоскости параллельной плоскости xОy и перпендикулярной оси Оz. Аналогично, при А = С = 0 плоскость перпендикулярна оси Оy и параллельна плоскости xOz, при В = С = 0 плоскость перпендикулярна оси Оx и параллельна плоскости yOz. Если в этих случаях и D = 0, то плоскость совпадает с соответствующей координатной плоскостью.
2. уравнение плоскости в отрезках Предположим, что в общем уравнении плоскости D ≠ 0, т.е. плоскость не проходит через начало координат. Преобразуем уравнение следующим образом: Ax + By + Cz = – D, разделим уравнение на (– D):
Обозначим
Это уравнение плоскости в отрезках.
С помощью уравнения плоскости в отрезках легко изобразить плоскость в прямоугольных декартовых координатах. Например, плоскость, заданная общим уравнением 2 x + 3 y + z – 6 = 0, преобразуется в уравнение в отрезках: 2 x + 3 y + z = 6 => Отметив точки с координатами (3, 0, 0), (0, 2, 0), (0, 0, 6), принадлежащие плоскости, можно начертить треугольник плоскости, отсекаемый координатными плоскостями (рис. 34).
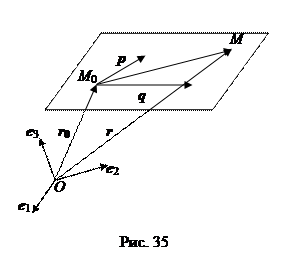
3. векторное и векторно-параметрическое уравнения плоскости Пусть задан базис е 1, е 2, е 3, тогда плоскость будет определена, если будут заданы два неколлинеарных вектора p и q и начальная точка М 0. (Не теряя общности, можно считать, что p и q приложены к точке М 0).
С другой стороны, обозначив через r 0 радиус-вектор точки М 0, а через r радиус-вектор точки М, получим r – r 0 = t 1 p + t 2 q. Это векторное уравнение плоскости. В базисе е 1, е 2, е 3 вектора r, r 0, p, q имеют координаты: r (x, y, z), r 0(x 0, y 0, z 0), p (p 1, p 2, p 3), q (q 1, q 2, q 3). Найдем координаты векторов векторного уравнения плоскости: r – r 0 = (x – x 0, y – y 0, z – z 0), t 1 p + t 2 q = (t 1 p 1 + t 2 q 1, t 1 p 2 + t 2 q 2, t 1 p 3 + t 2 q 3). Приравниваем соответствующие координаты и получаем:
Это параметрические уравнения плоскости.
4. уравнение плоскости, проходящей через три заданные точки Известно, что через три точки, не лежащие на одной прямой, проходит одна плоскость. Пусть заданы три точки M 1(x 1, y 1, z 1), M 2(x 2, y 2, z 2), и M 3(x 3, y 3, z 3). Произвольная точка М (x, y, z) лежит в той же плоскости, что и точки М 1, М 2, М 3, если все три вектора Таким образом, точка М лежит в плоскости М 1 М 2 М 3, если векторы ( Учитывая, что указанные векторы имеют координаты:
Смешанное произведение записывается в виде:
Это уравнение плоскости, проходящей через три заданные точки.
5. нормальное уравнение плоскости Рассмотрим общее уравнение плоскости: Ax + By + Cz + D = 0, где n (A, B, C) – вектор нормали. Разделим уравнение на
Обозначим
где cosα, cosβ, cosγ – направляющие косинусы вектора n, α, β, γ – углы, образованные вектором n и осями координат, получаем x cosα + y cosβ + z cosγ – p = 0. Это нормальное уравнение, р – длина перпендикуляра, опущенного из начала координат на плоскость, т.е. расстояние от начала координат до плоскости.
6. примеры решения типовых задач Рассмотрим связь между различными способами задания плоскости. Пример 1. Даны три точки А (1, 1, 1), В (2, 2, 0), С (3, 0, 1). Найдем уравнение плоскости (АВС). Запишем уравнение плоскости, проходящей через три заданные точки:
Разложим определитель по первой строке:
Вычислим определители: – (x – 1) – 2(y – 1) – 3(z – 1) = 0, – x – 2 y – 3 z + 6 = 0. Умножим уравнение на (–1), получим x + 2 y + 3 z – 6 = 0. Это общее уравнение плоскости. Убедимся, что это искомое уравнение плоскости, которая проходит через три точки. Для этого подставим координаты точек в уравнение: 1 + 2∙1 + 3∙1 – 6 = 0, 2 + 2∙2 + 3∙0 – 6 = 0, 3 + 2∙0 + 3∙1 – 6 = 0. Действительно, полученное уравнение превратилось в тождества. Следовательно, все три точки лежат на этой плоскости. Запишем уравнение плоскости в отрезках. x + 2 y + 3 z = 6 Делим это уравнение на 6, получаем
В качестве двух неколлинеарных направляющих векторов плоскости можно взять векторы
В качестве начальной точки выбираем точку А (1, 1, 1), ее координаты совпадают с координатами ее радиус-вектора r 0(1, 1, 1). Получаем, что в уравнении r – r 0 = t 1 p + t 2 q p = Запишем это векторно-параметрическое уравнение как параметрическое. Учитывая, что r – r 0 = (x – 1, y – 1, z – 1), t 1 p = t 1 t 2 q = t 2 и, приравнивая соответствующие координаты, получаем:
Это параметрическое уравнение плоскости. Вернемся к общему уравнению плоскости x + 2 y + 3 z – 6 = 0. Умножим уравнение на нормирующий множитель
Это нормальное уравнение плоскости. Здесь направляющие косинусы: Пример 2. Определить расстояние от точки М (3, 5, –8) до плоскости 6 x – 3 y + 2 z – 28 = 0. Рассмотрим задачу в общем виде. Дана точка M 1(x 1, y 1, z 1) и плоскость α: Ax + By + Cz + D = 0. Требуется найти расстояние от точки М 1 до плоскости. Расстояние d от точки М 1 до плоскости измеряется длиной перпендикуляра, опущенного из точки на плоскость: d = где K (x 0, y 0, z 0) – точка, принадлежащая плоскости α. Так как векторы
так как угол φ равен 0º или 180º. Учитывая, что n = (A, B, C),
= Ax 1 + By 1 + Cz 1 + D – Ax 0 – By 0 – Cz 0 – D = = (Ax 1 + By 1 + Cz 1 + D) – (Ax 0 + By 0 + Cz 0 + D). Выражение Ax 0 + By 0 + Cz 0 + D = 0, так как точка K (x 0, y 0, z 0) лежит на плоскости α и ее координаты удовлетворяют уравнению плоскости. Имеем
Отсюда получаем важную для решения задачи формулу:
Таким образом, чтобы найти расстояние от точки M 1(x 1, y 1, z 1) до плоскости Ax + By + Cz + D = 0, нужно в левую часть уравнения вместо текущих координат x, y, z подставить координаты точки M 1(x 1, y 1, z 1) и разделить полученное число на модуль вектора нормали | n |, взяв результат по абсолютной величине. Вернемся к поставленной задаче. Подставим координаты точки М (3, 5, –8) в уравнение плоскости 6 x – 3 y + 2 z – 28 = 0 и разделим на модуль нормали:
Пример 3. Составить уравнение плоскости, проходящей через точку М (2, 3, 5) и перпендикулярной вектору 4 i + 3 j + 2 k. Данный вектор можно рассматривать как вектор нормали искомой плоскости, общее уравнение которой имеет вид: 4 x + 3 y + 2 z + D = 0. Для определения значения свободного члена подставим координаты точки М в уравнение: 4∙2 + 3∙3 + 2∙ 5 + D = 0, 8 + 9 + 10 + D = 0, D = –27. Теперь можно записать уравнение искомой плоскости: 4 x + 3 y + 2 z – 27 = 0. Пример 4. Составить уравнение плоскости, проходящей через точки M 1(1,–2, 6), M 2(5, –4, –2) и отсекающей равные отрезки на осях Ox и Oy. Будем искать уравнение плоскости в виде:
По условию a = b, поэтому уравнение можно переписать иначе:
Подставляя координаты точек M 1(1, –2, 6), M 2(5, –4, –2) в последнее уравнение, получим
Решаем систему полученных уравнений:
Подставляем значение c = 2 во второе уравнение:
Следовательно, искомое уравнение имеет вид
Пример 5. Составить уравнение плоскости, проходящей через точку М (3, 2, 1) параллельно плоскости 3 x – 5 y + 2 z – 6 = 0. Очевидно, что вектор нормали к плоскости 3 x – 5 y + 2 z – 6 = 0 будет перпендикулярен и искомой плоскости, параллельной данной. Его координаты: n (3, –5, 2). Следовательно, искомая плоскость имеет уравнение 3 x – 5 y + 2 z + D = 0. Для определения значения свободного члена подставим в уравнение координаты точки М: 3∙3 – 5∙2 + 2∙ 1 + D = 0, 9 – 10 + 2 + D = 0, D = –1. Значит, требуемое уравнение: 3 x – 5 y + 2 z – 1 = 0. Пример 6. Найти уравнение плоскости, проходящей через точки M 1(1, 2, –1), M 2(3, 5, 1) перпендикулярно плоскости 3 x + 5 y – z + 7 = 0. Очевидно, что нормальный вектор данной плоскости n (3, 5, –1) будет параллелен искомой плоскости, а вектор n 1 = [ n, = Уравнение плоскости будет 13 x – 8 y – z + D = 0. Найдем D, для этого подставим координаты, например, точки М 1, получим 13∙1 – 8∙2 – (–1) + D = 0 => 13 – 16 + 1 + D = 0 => D = 2. Окончательно имеем требуемое уравнение: 13 x – 8 y – z + 2 = 0. Пример 7. Составить уравнение плоскости, проходящей через точку М (3, –1, 2) и перпендикулярной плоскостям 3 x + 5 y – 2 z + 7 = 0 и x – 2 y + 3 z + 6 = 0. Очевидно, что нормали данных плоскостей n 1(3, 5, –2) и n 2(1, –2, 3) будут параллельны искомой плоскости и, значит, за нормаль к ней можно взять их векторное произведение. n = [ n 1, n 2] = = Уравнение принимает вид 11 x – 11 y – 11 z + D = 0. Разделим его на 11, получим x – y – z + D ` = 0. Подставим в это уравнение координаты точки М (3, –1, 2), найдем D ′: 3 + 1 – 2 + D ′ = 0 => D ′ = –2. Требуемое уравнение: x – y – z – 2 = 0. Дата добавления: 2015-01-18 | Просмотры: 2309 | Нарушение авторских прав |
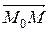 перпендикулярен вектору n и, значит, их скалярное произведение равно нулю. Учитывая, что
перпендикулярен вектору n и, значит, их скалярное произведение равно нулю. Учитывая, что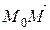 (x – x 0, y – y 0, z – z 0) и n (A, B, C),
(x – x 0, y – y 0, z – z 0) и n (A, B, C),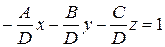 =>
=> 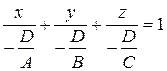 .
.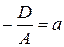 ,
, 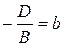 ,
, 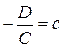 , получим
, получим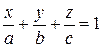 .
.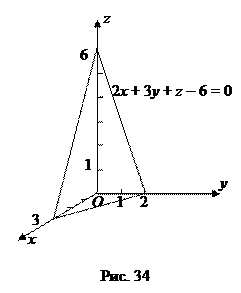 Выясним геометрический смысл входящих в уравнение параметров. Пусть y = z = 0, тогда
Выясним геометрический смысл входящих в уравнение параметров. Пусть y = z = 0, тогда 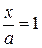 и x = a, следовательно, плоскость проходит через точку с координатами (а, 0, 0). Аналогично, полагая x = y = 0, получаем z = c и соответственно точку (0, 0, с), принадлежащую плоскости. Если x = z = 0, то y = b и точка с координатами (0, b, 0) лежит на плоскости. Полученные точки (a, 0, 0), (0, b, 0), (0, 0, c) – точки пересечения плоскости с координатными осями. Следовательно, a, b, c – это длины отрезков, отсекаемых плоскостью на осях координат, взятые со знаком плюс или минус в зависимости от того, в какой части оси произошло пересечение.
и x = a, следовательно, плоскость проходит через точку с координатами (а, 0, 0). Аналогично, полагая x = y = 0, получаем z = c и соответственно точку (0, 0, с), принадлежащую плоскости. Если x = z = 0, то y = b и точка с координатами (0, b, 0) лежит на плоскости. Полученные точки (a, 0, 0), (0, b, 0), (0, 0, c) – точки пересечения плоскости с координатными осями. Следовательно, a, b, c – это длины отрезков, отсекаемых плоскостью на осях координат, взятые со знаком плюс или минус в зависимости от того, в какой части оси произошло пересечение.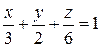 .
. Произвольная точка М лежит на плоскости, если вектор
Произвольная точка М лежит на плоскости, если вектор 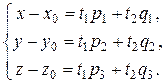
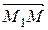 ,
, 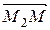 ,
, 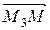 лежат в одной плоскости.
лежат в одной плоскости.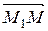 ,
, 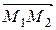 ,
, 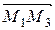 коллинеарны и, следовательно, их смешанное произведение равно нулю,
коллинеарны и, следовательно, их смешанное произведение равно нулю,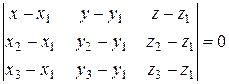 .
.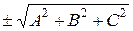 , знак выбираем противоположный знаку свободного члена D. Уравнение приобретает вид:
, знак выбираем противоположный знаку свободного члена D. Уравнение приобретает вид: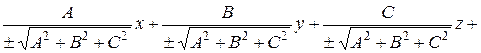
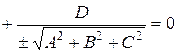 .
.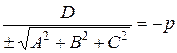 (p > 0), учитывая, что
(p > 0), учитывая, что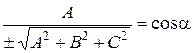 ,
, 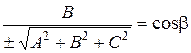 ,
, 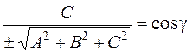 ,
,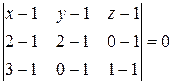 ,
,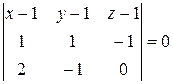 .
.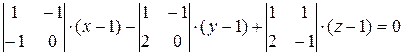 .
.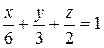 .
.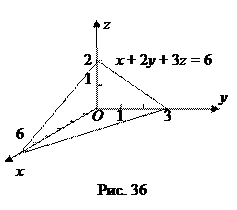 Очевидно, что плоскость отсекает по оси Оx отрезок длиной 6 единиц, по оси Oy отрезок длиной 3 и по оси Oz отрезок в 2 единицы. Теперь нетрудно изобразить эту плоскость в декартовой системе координат (рис. 36).
Очевидно, что плоскость отсекает по оси Оx отрезок длиной 6 единиц, по оси Oy отрезок длиной 3 и по оси Oz отрезок в 2 единицы. Теперь нетрудно изобразить эту плоскость в декартовой системе координат (рис. 36).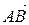 и
и 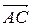 . Для того чтобы найти координаты вектора нужно из координат конца вектора вычесть соответствующие координаты начала:
. Для того чтобы найти координаты вектора нужно из координат конца вектора вычесть соответствующие координаты начала: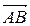 (1, 1, –1),
(1, 1, –1),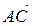 (2, –1, 0).
(2, –1, 0).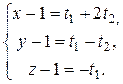
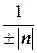 , где n – вектор нормали. В данном случае n (1, 2, 3), тогда
, где n – вектор нормали. В данном случае n (1, 2, 3), тогда 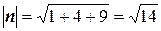 . Знак нормирующего множителя выбираем противоположный знаку свободного члена (–6). Получаем уравнение
. Знак нормирующего множителя выбираем противоположный знаку свободного члена (–6). Получаем уравнение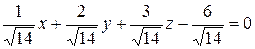 .
.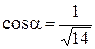 ,
, 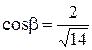 ,
, 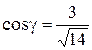 , где α, β, γ – углы, образованные вектором нормали с соответствующими осями координат,
, где α, β, γ – углы, образованные вектором нормали с соответствующими осями координат, 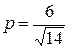 – расстояние от начала координат до плоскости АВС.
– расстояние от начала координат до плоскости АВС.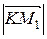 ,
,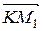 и n коллинеарны, то их скалярное произведение имеет вид
и n коллинеарны, то их скалярное произведение имеет вид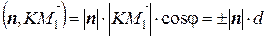 ,
,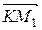 = (x 1 – x 0, y 1 – y 0, z 1 – z 0), запишем скалярное произведение через координаты сомножителей:
= (x 1 – x 0, y 1 – y 0, z 1 – z 0), запишем скалярное произведение через координаты сомножителей: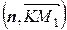 = A (x 1 – x 0) + B (y 1 – y 0) + C (z 1 – z 0),
= A (x 1 – x 0) + B (y 1 – y 0) + C (z 1 – z 0),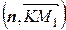 = Ax 1 + By 1 + Cz 1 – Ax 0 – By 0 – Cz 0 =
= Ax 1 + By 1 + Cz 1 – Ax 0 – By 0 – Cz 0 =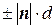 = Ax 1 + By 1 + Cz 1 + D.
= Ax 1 + By 1 + Cz 1 + D.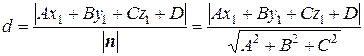 .
.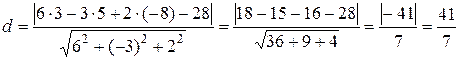 .
.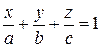 .
.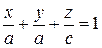 .
.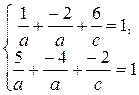 или
или 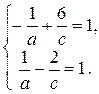
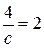 => c = 2.
=> c = 2.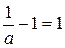 =>
=> 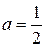 .
.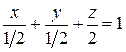 или 4 x + 4 y + z – 2 = 0.
или 4 x + 4 y + z – 2 = 0.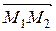 = (2, 3, 2) лежит в искомой плоскости, и, значит, их векторное произведение будет перпендикулярно искомой плоскости и может рассматриваться как нормаль.
= (2, 3, 2) лежит в искомой плоскости, и, значит, их векторное произведение будет перпендикулярно искомой плоскости и может рассматриваться как нормаль.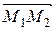 ] =
] = 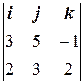 =
=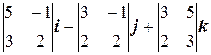 = 13 i – 8 j – k.
= 13 i – 8 j – k.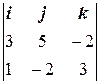 =
=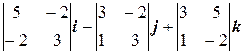 = 11 i – 11 j – 11 k.
= 11 i – 11 j – 11 k.