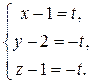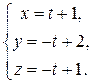 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Прямая в пространстве
1. векторно-параметрическое и параметрические уравнения прямой в пространстве Пусть в трехмерном пространстве задан вектор q (q 1, q 2, q 3) и точка M 0(x 0, y 0, z 0). Требуется записать уравнение прямой, параллельной заданному вектору q, который является направляющим, и проходящей через начальную точку М 0.
Если обозначить через r 0 радиус-вектор точки М 0, а через r радиус-вектор точки М, то
и, следовательно, r – r 0 = t q. Это векторно-параметрическое уравнение прямой в пространстве. По внешнему виду это уравнение неотличимо от векторно-параметрического уравнения прямой на плоскости. Отличие состоит в том, что на плоскости вектора r, r 0, q имеют две координаты, а в пространстве – три. Учитывая, что координаты радиус-вектора и соответствующей точки одинаковы, получаем r (x, y, z), r 0(x 0, y 0, z 0) и, следовательно, r – r 0 = (x – x 0, y – y 0, z – z 0), t q = (q 1 t, q 2 t, q 3 t), приравниваем соответствующие координаты:
Полученная система представляет собой векторные уравнения прямой в пространстве. 2. каноническое уравнение прямой в пространстве Рассмотрим векторное уравнение прямой. Предположим, что координаты направляющего вектора отличны от нуля q 1 ≠ 0, q 2 ≠ 0, q 3 ≠ 0. Выразим параметр t из уравнений
Получим
и, значит
Это каноническое уравнение прямой в пространстве. Пусть q 1 = 0, q 2 ≠ 0, q 3 ≠ 0, векторные уравнения имеют вид
и, выражая t, получаем равенства
Аналогично, при q 1 ≠ 0, q 2 = 0, q 3 ≠ 0, получаем
И при q 1 ≠ 0, q 2 ≠ 0, q 3 = 0
Таким образом, при равенстве нулю какой-либо координаты направляющего вектора, приравниваем к нулю соответствующий числитель в каноническом уравнении.
3. уравнение прямой, проходящей через две заданные точки Пусть даны точки M 1(x 1, y 1, z 1) и M 2(x 2, y 2, z 2). Требуется записать уравнение прямой, проходящей через М 1 и М 2. В качестве направляющего вектора можно взять
Это уравнение прямой, проходящей через две заданные точки в пространстве. Очевидно, что если x 2 = x 1, то уравнение имеет вид
При y 2 = y 1 и при z 2 = z 1 аналогично.
4. задание прямой как пересечение двух плоскостей Очевидно, что две плоскости в пространстве пересекаются по прямой. Две плоскости пересекаются, если нормальные векторы не являются коллинеарными. Таким образом, систему
в случае если n 1(A 1, B 1, C 1) и n 2(A 2, B 2, C 2) неколлинеарны, можно рассматривать как способ задания прямой в пространстве. Заметим, что прямая лежит в первой плоскости и, значит, нормаль n 1 ей перпендикулярна, аналогично, из того, что прямая лежит и во второй плоскости, следует, что нормаль n 2 ей тоже перпендикулярна. Мы нашли два вектора, перпендикулярные прямой, для того, чтобы найти вектор, параллельный прямой возьмем векторное произведение векторов n 1 и n 2. Таким образом, направляющий вектор прямой q можно найти по формуле q = [ n 1, n 2] = Очевидно, что любая прямая в пространстве пересекает, по крайней мере, одну из координатных плоскостей и, значит, по крайней мере, одна из систем
будет иметь решение, которое можно рассматривать как начальную точку прямой. Это позволяет переходить от уравнений прямой, заданных как пересечение двух плоскостей, к каноническому, параметрическому, векторно-параметрическому уравнениям.
5. примеры решения типовых задач Пример 1. Найти, если возможно, параметрические, каноническое уравнения, уравнение прямой, проходящей через две заданные точки (точки пересечения с координатными плоскостями) для прямой, заданной как пересечение двух плоскостей:
Нормали к плоскостям имеют координаты n 1(2, 1, –2) и n 2(1, 2, –1). Найдем направляющий вектор прямой. q = [ n 1, n 2] =
Найдем точки пересечения прямой с координатными плоскостями:
Получили, что точка (0, 1, 0) является точкой пересечения прямой и с плоскостью yOz (x = 0) и с плоскостью xOy (z = 0), так как эта точка лежит на оси Oy. Полученная точка может рассматриваться как начальная точка прямой М 0(0, 1, 0) и, зная направляющий вектор q (3, 0, 3), можем записать параметрическое и каноническое уравнения
Умножим первое уравнение на 3, получим x = z, y = 1. Запишем параметрические уравнения
учитывая, что t – произвольный параметр, то 3 t также принимает все значения на числовой прямой, можно переписать
Эта система представляет собой параметрические уравнения прямой. Найдем точку пересечения прямой с плоскостью xOz (y = 0). Для этого решим систему
Разделим первое уравнение системы на 2, получим
Очевидно, что первые два уравнения противоречивы и, значит, система несовместна. Следовательно, прямая плоскость xOz не пересекает, а плоскости xOy и yOz пересекает в одной точке на оси Oy, и, значит, невозможно записать уравнение этой прямой как прямой, проходящей через две заданные точки, если за точки предлагают взять точки пересечения с координатными плоскостями. Пример 2. Записать параметрические уравнения прямой, проходящей через точки М 1(1, 2, 3) и М 2(3, 0, 1). Запишем уравнение прямой, проходящей через две заданные точки:
Умножим полученное уравнение на 2. Получим
Пусть эти равенства равны некоторому параметру t:
тогда
Это можно переписать в виде
Полученная система представляет собой параметрические уравнения прямой.
Дата добавления: 2015-01-18 | Просмотры: 717 | Нарушение авторских прав |
Произвольная точка M (x, y, z) лежит на прямой тогда и только тогда, когда вектор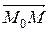 
коллинеарен вектору q (рис. 37). А это значит, что для любой M (x, y, z) найдется значение параметра t такое, что
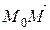= t q.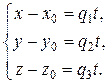
, 
, 
.
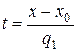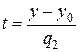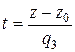
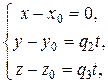
и x = x 0.
и y = y 0.
и z = z 0.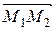
= (x 2 – x 1, y 2 – y 1, z 2 – z 1), а в качестве начальной точки любую из точек, например, М 1. Запишем каноническое уравнение
.
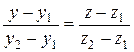, x = x 1.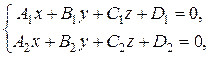
.
=
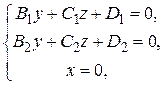
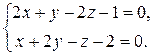
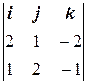3 i + 3 k = (3, 0, 3).
=> 
=> 
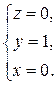
, y = 1.
, y = 1.
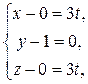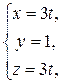
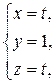
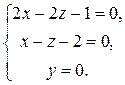
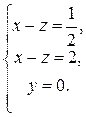
или 
или 
или 
.
.
,
или 
