 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
На плоскости и в пространствеВ курсе линейной алгебры было дано понятие линейной зависимости векторов для произвольного n -мерного векторного пространства. Напомним его. Определение 8. Система векторов а 1, а 2, …, аk является линейно зависимой, если найдется нетривиальная линейная комбинация векторов α1 а 1 + α2 а 2 + … + α k аk равная нулевому вектору. Мы дали запись векторов без стрелочек и, не выделяя жирным шрифтом, подчеркнув тем самым, что это вектора произвольного n -мерного векторного пространства. Нетривиальная линейная комбинация векторов – это алгебраическая сумма векторов α1 а 1 + α2 а 2 + … + α k аk c некоторыми коэффициентами α1, α2, …,α k, где хотя бы один отличен от нуля. Кроме этого определения было дано еще одно эквивалентное определение линейной зависимости векторов. Определение 9. Система векторов а 1, а 2, …, аk называется линейно зависимой, если один из векторов можно представить в виде линейной комбинации остальных векторов. Рассматривая вектора на прямой, плоскости и в пространстве с учетом введенных операций сложения и умножения на число, можно составлять суммы векторов, умноженных на некоторые коэффициенты α1 а 1 + α2 а 2 + … + α k а k. Такие суммы будем называть линейными комбинациями. Линейные комбинации векторов обладают следующими очевидными свойствами: если векторы а 1, а 2, …, а k коллинеарны, то любая их линейная комбинация им коллинеарна; если векторы а 1, а 2, …, а k компланарны, то любая их линейная комбинация с ними компланарна. Это следует из того, что вектор α а коллинеарен вектору а, а сумма векторов лежит в той же плоскости, что и слагаемые. Пусть на прямой дан единичный вектор, т. е. вектор, который принят за единицу измерения длин, а его направление объявлено положительным на всей этой прямой. Можно сказать, что наша прямая превращена в ось. Определение 10. Отношение длин любого вектора а на данной оси к длине единичного вектора, взятое со знаком «+», если вектора направлены в одну сторону, и со знаком «–», если вектора противоположно направлены, называется координатой вектора а на данной оси. (Также используются синонимы: компонента, алгебраическое значение вектора.) Пусть дан вектор 1. Два вектора на данной прямой равны тогда и только тогда, когда равны их координаты. 2. Если два вектора имеют одну и ту же длину, но противоположны по направлению, то их координаты имеют один и тот же модуль, но противоположны по знаку: (АВ) + (ВА) = 0. 3. Координата единичного вектора равна 1. 4. При любом расположении точек А, В и С на оси имеет место числовое равенство (АВ) + (ВС) = (АС). При рассмотрении n -мерных векторных пространств, было введено понятие базиса. Мы определяли базис как максимальную линейно независимую систему векторов. Максимальность понимается в том смысле, что если к системе добавить любой вектор, она станет линейно зависимой. Кроме того, в курсе алгебры доказывалось утверждение, что если система векторов линейно независима и любой вектор векторного пространства можно представить в виде линейной комбинации векторов системы, то данная система векторов является базисом. Как видно из определения координатной оси, на прямой базисом является любой ненулевой вектор. Определение 11. Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке. Базисом на плоскости называются два неколлинеарных вектора на этой плоскости, взятые в определенном порядке. Если вектор представлен как линейная комбинация некоторых векторов, то говорят, что он разложен по этим векторам. Определение 12. Если е 1, е 2, е 3 – базис в пространстве и а разложен по базису с коэффициентами α1, α2, α3 а = α1 е 1 + α2 е 2 + α3 е 3, то числа α1, α2, α3 называются координатами вектора а в данном базисе в пространстве. Аналогично, если е 1, е 2 – базис на плоскости и вектор а разложен по этому базису а = α1 е 1 + α2 е 2 , то числа α1, α2 называются координатами вектора а в базисе е 1, е 2 на плоскости. Лемма 1. Координаты вектора на прямой, плоскости и в пространстве определяются однозначно. Доказательство. Докажем единственность разложения по базису для пространства. Пусть а = а 1 е 1 + а 2 е 2 + а 3 е 3 и а = а′ 1 е 1 + а′ 2 е 2 + а′ 3 е 3. Вычтем второе равенство из первого: а – а = (а 1 е 1 + а 2 е 2 + а 3 е 3) – (а′ 1 е 1 + а′ 2 е 2 + а′ 3 е 3) = = (а 1 – а′ 1) е 1 + (а 2 – а′ 2) е 2 + (а 3 – а′ 3) е 3 = 0. Мы получили линейную комбинацию базисных векторов е 1, е 2, е 3 равную нулю. Учитывая линейную независимость базисных векторов, получаем, что все коэффициенты линейной комбинации должны быть равны нулю, т.е. а 1 = а′ 1, а 2 = а′ 2, а 3 = а′ 3. Доказательство леммы для случая прямой и плоскости аналогично. Лемма доказана. Следствие. Равные векторы имеют одинаковый набор координат. Заметим, что при умножении вектора на число все его координаты умножаются на это число. Действительно, пусть а = а 1 е 1 + а 2 е 2 + а 3 е 3, тогда λ а = λ(а 1 е 1 + а 2 е 2 + а 3 е 3) = (λ а 1) е 1 + (λ а 2) е 2 + (λ а 3) е 3. При сложении векторов складываются их соответствующие координаты. Действительно, если а = а 1 е 1 + а 2 е 2 + а 3 е 3 и b = b 1 е 1 + b 2 е 2 + b 3 е 3, то a + b = (а 1 е 1 + а 2 е 2 + а 3 е 3) + (b 1 е 1 + b 2 е 2 + b 3 е 3) = = (а 1 + b 1) е 1 + (а 2 + b 2) е 2 + (а 3 + b 3) е 3. Понятие линейной зависимости векторов, играющее большую роль в алгебре, в курсе аналитической геометрии наполняется новым смыслом. Приведем для иллюстрации несколько утверждений. 1. Любые два коллинеарных вектора линейно зависимы, и наоборот, два линейно зависимых вектора коллинеарны. 2. Любые три компланарных вектора линейно зависимы, и наоборот, три линейно зависимых вектора компланарны. 3. Каждые четыре вектора линейно зависимы.
Дата добавления: 2015-01-18 | Просмотры: 892 | Нарушение авторских прав |
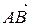 , тогда его координату на оси обозначим (AB). Из определения вытекают следующие свойства:
, тогда его координату на оси обозначим (AB). Из определения вытекают следующие свойства: