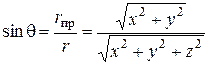|
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Деление отрезка в заданном отношении
1. аффинная система координат Зафиксируем на плоскости точку О (начало координат) и два вектора е 1 и е 2, приложенные к точке О. Вектора е 1, е 2 неколлинеарны и, следовательно, любой вектор плоскости разложим в линейную комбинацию по е 1 и е 2. Определение 13. Аффинная система координат на плоскости – это совокупность точки О и базиса е 1, е 2. Векторы е 1 и е 2 определяют две оси, пересекающиеся в точке О и являющиеся по определению единичными векторами этих осей. Первая ось называется осью абсцисс, вторая – осью ординат. Рассмотрим произвольную точку М. Вектор
т.е. координатами вектора Определение 14. Координаты точки М в аффинной системе координат – это координаты ее радиус-вектора
Аналогично, В (2; 0,5) и Таким же образом можно определить аффинную систему координат в пространстве. Пусть зафиксирована точка О и три вектора е 1, е 2, е 3, приложенные к О. Предполагается, что вектора е 1, е 2, е 3 некомпланарны, и, следовательно, образуют базис. К осям абсцисс и ординат, определенных векторами е 1 и е 2, добавляется ось аппликат, проходящая через вектор е 3. Раскладывая по базису е 1, е 2, е 3 радиус-вектор
В аффинной системе координат при сложении двух векторов складываются их соответствующие координаты, при умножении вектора на число координаты умножаются на это число.
Таким образом, для того чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.
2. деление отрезка в заданном отношении Пусть в системе координат даны точки А (xA, yA, zA) и B (xB, yB, zB). Пусть точка М (x, y, z) лежит на отрезке [ AB ] (рис. 5), причем выполняется условие
Рассмотрим вектора μ | Найдем координаты векторов μ μ λ Учитывая равенство μ μ(x – xA) = λ(xB – x), μ(y – yA) = λ(yB – y), μ(z – zA) = λ(zB – z). Раскроем скобки и перепишем равенства в виде μ x + λ x = μ xA + λ xB, μ y + λ y = μ yA + λ yB, μ z + λ z = μ zA + λ zB. Следовательно, получаем
Эти формулы задают координаты точки, которая делит отрезок [ AB ] в отношении λ: μ. Очевидно, что если отрезок лежит на плоскости, то точка М имеет только две координаты x и y, которые находятся по тем же формулам.
3. декартова прямоугольная система координат Из школьного курса математики видно, что наиболее распространенной является система координат, где базисные векторы имеют одинаковую длину на всех осях (единичный отрезок) и оси координат попарно образуют прямой угол. Определение 15. Базис называется ортонормированным, если любые его два различных вектора перпендикулярны, и длина любого базисного вектора равна единице. Система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.
Действительно, из рис. 6 видно, что отрезок AB является гипотенузой прямоугольного треугольника ABM, где катеты равны xB – xA и yB – yA. Поэтому указанная формула является следствием теоремы Пифагора | AB |2 = (xB – xA)2 + (yB – yA)2. Нетрудно сделать обобщение на случай, когда точки А и В лежат в пространстве:
Очевидно, если одна из точек отрезка совпадает с началом координат, а другая есть точка М (x, y, z), то
Следовательно, в декартовой прямоугольной системе координат для радиус-вектора | т.е. квадрат длины вектора равен сумме квадратов его координат.
4. полярная система координат Кроме декартовой прямоугольной системы на плоскости часто используется полярная система координат.
Положение произвольной точки М определяется длиной r радиус-вектора Длину радиус-вектора r = | Пусть начало координат прямоугольной декартовой системы совпадает с полюсом, а положительное направление оси Ox совпадает с полярной осью (рис. 8). Пусть дана некоторая точка М, которая в прямоугольной системе имеет координаты M (x, y) и в полярной – координаты M (r, φ). Установим взаимосвязь между декартовыми прямоугольными и полярными координатами.
x = r cos φ, y = r sin φ. В свою очередь, полярные координаты можно выразить через декартовы следующим образом:
В некоторых случаях кривые удобнее задавать в полярной системе координат. Например, уравнение окружности с центром в точке О и радиусом R, в полярной системе координат выглядит как r = R. Уравнение луча, исходящего из начала координат под углом φ0 к положительному направлению оси Ox задается в виде φ = φ0.
5. цилиндрическая система координат Цилиндрическая система представляет собой обобщение полярной системы координат для пространства.
Рассмотрим в пространстве декартову прямоугольную систему координат, плоскость xOy которой совмещена с полярной системой, т.е. начало координат – с полюсом, а положительное направление оси Ox – с полярной осью (рис. 9). Точка М имеет два набора координат M (x, y, z) и М (r, φ, z). Найдем связь между ними. Очевидно, что проекция точки М на плоскость xOy имеет координаты М пр(x, y, 0) в декартовой и М пр(r, φ) в полярной. При этом x = r cos φ, y = r sin φ. Следовательно, формулы перехода от цилиндрических координат имеют вид x = r cos φ, y = r sin φ, z = z. Обратные формулы перехода от декартовых координат к цилиндрическим:
z = z.
6. сферическая система координат
Установим связь между декартовыми координатами M (x, y, z) и сферическими М (r, φ, θ). По рисунку видно, что x = r пр cosφ, y = r пр sinφ, где r пр – длина проекции радиус-вектора x = r sinθ cosφ, y = r sinθ cosφ. Координату z можно найти из треугольника ОММ пр: z = r cosθ. Переход от декартовых координат к сферическим осуществляется по формулам: r пр =
Дата добавления: 2015-01-18 | Просмотры: 1535 | Нарушение авторских прав |
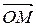 , соединяющий начало координат и точку М, называется радиус-вектором точки М. Разложим вектор
, соединяющий начало координат и точку М, называется радиус-вектором точки М. Разложим вектор 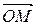 по базису е 1, е 2
по базису е 1, е 2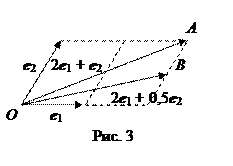 Заметим, что в определении аффинной системы координат не предполагается, что векторы е 1 и е 2 будут одинаковой длины, и угол между ними не обязан быть 90°. Например, на рис. 3 вектора базиса е 1, е 2 не перпендикулярны и имеют различные длины. Точка А имеет в этой системе координаты А (2; 1), так как ее радиус-вектор задается линейной комбинацией
Заметим, что в определении аффинной системы координат не предполагается, что векторы е 1 и е 2 будут одинаковой длины, и угол между ними не обязан быть 90°. Например, на рис. 3 вектора базиса е 1, е 2 не перпендикулярны и имеют различные длины. Точка А имеет в этой системе координаты А (2; 1), так как ее радиус-вектор задается линейной комбинацией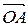 = 2 е 1 + е 2.
= 2 е 1 + е 2.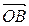 = 2 е 1 + 0,5 е 2.
= 2 е 1 + 0,5 е 2.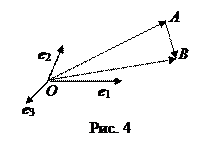 Пусть даны две точки А (xA, yA, zA) и B (xB, yB, zB). Тогда
Пусть даны две точки А (xA, yA, zA) и B (xB, yB, zB). Тогда 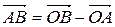 и, следовательно, вектор
и, следовательно, вектор 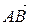 имеет координаты
имеет координаты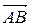 = (xB – xA, yB – yA, zB – zA).
= (xB – xA, yB – yA, zB – zA).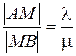 , где λ, μ > 0.
, где λ, μ > 0.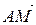 и
и 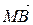 , учитывая, что λ, μ > 0, получаем
, учитывая, что λ, μ > 0, получаем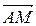 | = λ|
| = λ| 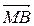 |, μ
|, μ 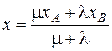 ;
;  ;
; 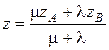 .
. Очевидно, что в декартовой прямоугольной системе координат на плоскости расстояние между точками A (xA, yA) и B (xB, yB) можно находить по формуле
Очевидно, что в декартовой прямоугольной системе координат на плоскости расстояние между точками A (xA, yA) и B (xB, yB) можно находить по формуле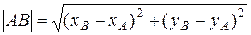 .
.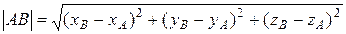 .
.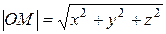 .
.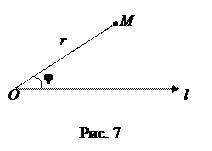 Определение 16. Полярная система координат – это совокупность точки О, называемой полюсом, и исходящего из полюса луча l, называемого полярной осью (рис. 7).
Определение 16. Полярная система координат – это совокупность точки О, называемой полюсом, и исходящего из полюса луча l, называемого полярной осью (рис. 7). Треугольник ОАМ прямоугольный, поэтому
Треугольник ОАМ прямоугольный, поэтому ,
,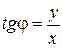 .
. Пусть на плоскости задана полярная система координат, тогда для произвольной точки М в пространстве можно определить ее проекцию на плоскость М пр, где М пр будет иметь координаты М пр(r, φ). Положение точки М определяется однозначно, если к положению М пр добавить высоту z точки М над проекцией. Поэтому координаты М в цилиндрической системе координат имеют вид М (r, φ, z).
Пусть на плоскости задана полярная система координат, тогда для произвольной точки М в пространстве можно определить ее проекцию на плоскость М пр, где М пр будет иметь координаты М пр(r, φ). Положение точки М определяется однозначно, если к положению М пр добавить высоту z точки М над проекцией. Поэтому координаты М в цилиндрической системе координат имеют вид М (r, φ, z).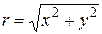 ,
,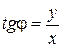 .
.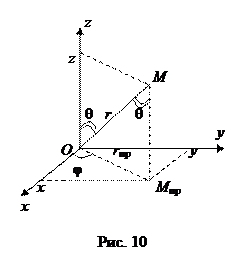 Пусть в пространстве задана декартова прямоугольная система координат. Положение точки M (x, y, z) однозначно определится, если мы зададим длину радиус-вектора r точки М, угол θ, который радиус-вектор образует с положительным направлением оси Oz, и угол φ, который проекция радиус-вектора образует с положительным направлением оси Ох (рис. 10). Эти три параметра (r, φ, θ) являются сферическими координатами точки М.
Пусть в пространстве задана декартова прямоугольная система координат. Положение точки M (x, y, z) однозначно определится, если мы зададим длину радиус-вектора r точки М, угол θ, который радиус-вектор образует с положительным направлением оси Oz, и угол φ, который проекция радиус-вектора образует с положительным направлением оси Ох (рис. 10). Эти три параметра (r, φ, θ) являются сферическими координатами точки М.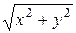 , r =
, r = 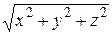 ,
,