 |
|
АкушерствоАнатомияАнестезиологияВакцинопрофилактикаВалеологияВетеринарияГигиенаЗаболеванияИммунологияКардиологияНеврологияНефрологияОнкологияОториноларингологияОфтальмологияПаразитологияПедиатрияПервая помощьПсихиатрияПульмонологияРеанимацияРевматологияСтоматологияТерапияТоксикологияТравматологияУрологияФармакологияФармацевтикаФизиотерапияФтизиатрияХирургияЭндокринологияЭпидемиология |
Примеры решения типовых задач
В данном параграфе рассмотрим задачи, связанные с различными системами координат, делением отрезка в заданном отношении. Пример 1. Даны координаты точек: А (4; 3), В (7; 6), С (2; 11). Докажем, что треугольник АВС прямоугольный. Найдем длины сторон треугольника АВС. С этой целью используем формулу, позволяющую находить расстояние между двумя точками на плоскости:
Длины сторон будут равны:
Учитывая, что для сторон данного треугольника выполняется теорема Пифагора
то треугольник АВС – прямоугольный. Пример 2. Даны точки А (2; 1) и В (8; 4). Найдем координаты точки М (х; у), которая делит отрезок в отношении 2:1. Напомним, что точка М (х; у) делит отрезок АВ, где A (xA, yA), B (xB, yB), в отношении λ: μ, если ее координаты удовлетворяют условиям:
Найдем точку М для данного отрезка
Таким образом, точка М (6; 3) делит отрезок АВ в отношении 2:1. Пример 3. Найдем прямоугольные координаты точки А ( Учитывая формулы перехода от полярной к прямоугольной системе координат x = r cosφ, y = r sinφ, получаем
В прямоугольной декартовой системе координат координаты точки А (–2; 2). Пример 4. Найдем полярные координаты точек, имеющих следующие прямоугольные координаты: А ( Используем формулы перехода от прямоугольных координат к полярным:
Получим координаты для точки А:
Таким образом А (4; π/6) – полярные координаты (рис. 15). Для точки В (рис. 16) имеем
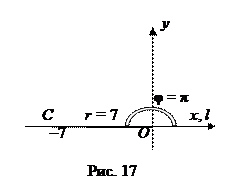
Следовательно, полярные координаты точки В ( Рассмотрим точку С (–7; 0) (рис. 17). В этом случае
Можно записать полярные координаты точки С (7; π).
Пример 5. Найдем длину вектора a = 20 i + 30 j – 60 k и его направляющие косинусы. Напомним, что направляющие косинусы – это косинусы углов, которые вектор a (a 1, a 2, a 3) образует с осями координат:
где Применим эти формулы к данному вектору, получим
Пример 6. Нормируем вектор a = 3 i + 4 j – 12 k. Нормировать вектор – это найти вектор единичной длины а 0, направленный также как и данный вектор. Для произвольного вектора a (a 1, a 2, a 3) соответствующий вектор единичной длины можно найти, умножив a на дробь
В нашем случае
Пример 7. Найдем скалярное произведение векторов a = 4 i + 5 j + 6 k и b = 3 i – 4 j + k. Для того чтобы найти скалярное произведение векторов, нужно умножить соответствующие координаты и полученные произведения сложить. Так, для векторов a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k скалярное произведение имеет вид: (a, b) = a 1 b 1 + a 2 b 2 + a 3 b 3. Для данных векторов получаем (a, b) = 4∙3 + 5∙(–4) + 6∙1 = 12 – 20 + 6 = –2. Пример 8. Покажем, что векторы a = 2 i – 3 j + 5 k и b = i + 4 j + 2 k перпендикулярны. Два вектора перпендикулярны, если их скалярное произведение равно нулю. Найдем скалярное произведение: (a, b) = 2∙1 + (–3)∙4 + 5∙2 = 2 – 12 + 10 = 0. Таким образом, векторы а и b перпендикулярны. Пример 9. Выясним, при каком значении параметра m векторы a = 2 i + 3 j + m k и b = 3 i + m j – 2 k перпендикулярны. Найдем скалярное произведение векторов а и b: (a, b) = 2∙3 + 3∙ m – 2∙ m = 6 + m. Векторы перпендикулярны, если их скалярное произведение равно нулю. Приравниваем к нулю произведение (а, b): 6 + m = 0. При m = – 6 векторы а и b перпендикулярны. Пример 10. Найдем скалярное произведение (3 а + 4 b, 2 а – 3 b), если | a | = 2, | b | = 1 и угол φ между а и b равен π/3. Воспользуемся свойствами скалярного произведения: (α a, β b) = αβ(a, b), (a + b, c) = (a, c) + (b, c), (a, b) = (b, a) (a, a) = | a |2, а также определением скалярного произведения (a, b) = | a |∙| b |∙cosφ. Перепишем скалярное произведение в виде (3 a + 4 b, 2 a – 3 b) = 6(a, a) – 9(a, b) + 8(b, a) – 12(b, b) = = 6| a |2 – (a, b) – 12| b |2 = 6∙22 – 2∙1∙cos(π/3) – 12∙12 = 11. Пример 11. Определим угол между векторами a = i + 2 j + 3 k и b = 6 i + 4 j – 2 k. Для нахождения угла воспользуемся определением скалярного произведения двух векторов (a, b) = | a |∙| b |∙cosφ, где φ – угол между векторами а и b. Выразим cosφ из этой формулы
Учитывая, что (а, b) = 1∙6 + 2∙4 + 3∙(–2) = 8,
Следовательно, Пример 12. Найдем векторное произведение векторов a = 5 i – 2 j + 3 k и b = i + 2 j – 4 k. Известно, что векторное произведение векторов a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k находится по формуле
Следовательно, для данных векторов
= 2 i + 23 j + 12 k. Рассмотрим пример, где для нахождения модуля векторного произведения будет использоваться определение векторного произведения, а не выражение его через координаты сомножителей, как было в предыдущем примере. Пример 13. Найдем модуль векторного произведения векторов а + 2 b и 2 а – 3 b, если | a | = 1, | b | = 2 и угол между векторами а и b равен 30°. Из определения векторного произведения видно, что для произвольных векторов а и b его модуль равен |[ a, b ] | = | a | ∙ | b | ∙ sin φ. Учитывая свойства векторного произведение [ a, b ] = – [ b, a ], [ a, a ] = 0, [α a + β b, c ] = α[ a, c ] + β[ b, c ], получаем [ a + 2 b, 2 a – 3 b ] = 2[ a, a ] – 3[ a, b ] + 4[ b, a ] – 6[ b, b ] = –7[ a, b ]. Значит, модуль векторного произведения равен |[ a + 2 b, 2 a – 3 b ]| = |–7[ a, b ]| = 7 ∙ | a | ∙ | b | ∙ sin 30° = 7∙1∙2∙0,5 = 7. Пример 14. Вычислим площадь параллелограмма, построенного на векторах a = 6 i + 3 j – 2 k и b = 3 i – 2 j + 6 k. Известно, что модуль векторного произведения двух векторов равен площади параллелограмма, построенного на этих векторах. Найдем векторное произведение по формуле:
где a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. Затем вычислим его модуль. Для данных векторов получаем
= 14 i – 42 j – 21 k. Следовательно, площадь параллелограмма равна S = |[ a, b ]| = Пример 15. Вычислим площадь треугольника с вершинами А (1;2;1), В (3;3;4), С (2;1;3). Очевидно, что площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах В свою очередь, площадь параллелограмма, построенного на векторах
Найдем координаты векторов
Найдем векторное произведение: [ Найдем модуль векторного произведения: |[ Следовательно, можем получить площадь треугольника:
Пример 16. Вычислим площадь параллелограмма, построенного на векторах a + 3 b и 3 a – b, если | a | = 2, | b | = 1 и угол между а и b равен 30°. Найдем модуль векторного произведения, используя его определение и свойства, указанные в примере 13, получим [ a + 3 b, 3 a – b ] = 3[ a, a ] – [ a, b ] + 9[ b, a ] – 3[ b, b ] = –10[ a, b ]. Значит, искомая площадь равна S = |[ a + 3 b, 3 a – b ]| = |–10[ a, b ]| = 10 ∙ | a | ∙ | b | ∙ sin 30° = = 10∙2∙1∙0,5 = 10 (кв. ед.). Следующие примеры будут связаны с использованием смешанного произведения векторов. Пример 17. Показать, что векторы a = i + 2 j – k, b = 3 i + k и с = 5 i + 4 j – k компланарны. Векторы компланарны, если их смешанное произведение равно нулю. Для произвольных векторов a = a 1 i + a 2 j + a 3 k, b = b 1 i + b 2 j + b 3 k, c = c 1 i + c 2 j + c 3 k смешанное произведение находим по формуле:
Для данных векторов получаем
Таким образом, данные векторы компланарны. Пример18. Найдем объем треугольной пирамиды с вершинами А (1;1;1), В (3;2;1), С (2;4;3), D (5;2;4). Найдем координаты векторов
Известно, что объем пирамиды равен 1/6 объема параллелепипеда, построенного на векторах
В свою очередь, объем параллелепипеда равен модулю смешанного произведения Vпарал = |( Найдем смешанное произведение ( Итак, объем пирамиды равен
В следующих примерах покажем возможное применение векторной алгебры. Пример 19. Проверим, являются ли коллинеарными вектора 2 а + b и а – 3 b, где a = 2 i + j – 3 k и b = i + 2 j + 4 k. Найдем координаты векторов 2 а + b и а – 3 b: 2 а + b = 2(2 i + j – 3 k) + i + 2 j + 4 k = 5 i + 4 j – 2 k, а – 3 b = 2 i + j – 3 k – 3(i + 2 j + 4 k) = – i – 5 j – 15 k. Известно, что у коллинеарных векторов пропорциональные координаты. Учитывая, что
получаем, что вектора 2 а + b и а – 3 b неколлинеарны. Эту задачу можно было решить и другим способом. Критерием коллинеарности векторов является равенство нулю векторного произведения: [2 a + b, a – 3 b ] = 2[ a, a ] – 6[ a, b ] + [ b, a ] – 3[ b, b ] = –7[ a, b ]. Найдем векторное произведение векторов а и b:
= 10 i – 11 j + 3 k ≠ 0. Следовательно, [2 a + b, a – 3 b ] = –7[ a, b ] ≠ 0 и векторы 2 а + b и а – 3 b неколлинеарны. Пример 20. Найдем работу силы F (3; 2; 1), когда точка ее приложения А (2; 4;–6), двигаясь прямолинейно, перемещается в точку В (5; 2; 3). Известно, что работа силы – это скалярное произведение силы F на вектор перемещения Найдем координаты вектора
Следовательно, работа силы F по перемещению точки А в точку В будет равна скалярному произведению (F, Пример 21. Пусть сила F (2;3;–1) приложена к точке А (4;2;3). Под действием силы F точка А перемещается в точку В (3;1;2). Найдем модуль момента силы F относительно точки В. Известно, что момент силы равен векторному произведению силы на перемещение. Найдем вектор перемещения
Найдем момент силы как векторное произведение:
= – 4 i + 3 j + k. Следовательно, модуль момента силы равен модулю векторного произведения: |[ F,
Вопросы для самопроверки 1. Что называется вектором? 2. Какие возможны линейные операции над векторами? 3. Какие векторы называются коллинеарными, компланарными? 4. Что такое линейная зависимость векторов? 5. Какие векторы образуют базис? 6. Описать системы координат. 7. Дать определение скалярного произведения, каковы его свойства. 8. Как вычислить скалярное произведение, зная координаты векторов? 9. Какие тройки векторов называются правыми? 10. Что называется векторным произведением? 11. Как определяется смешанное произведение? 12. 13. Каковы условия ортогональности, коллинеарности, компланарности? 14. Какими геометрическими свойствами обладают векторное и смешанное произведения? Дата добавления: 2015-01-18 | Просмотры: 12423 | Нарушение авторских прав |
 .
.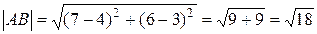 ,
,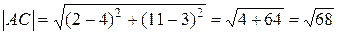 ,
, .
. ,
, ,
,  .
. ,
,  .
. 3π/4), если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.
3π/4), если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс.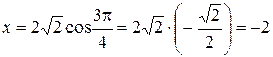 ,
,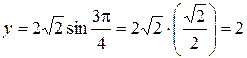 .
. ; 2), В (–4; 4), С (–7; 0).
; 2), В (–4; 4), С (–7; 0).
 ,
, .
. ,
,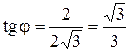 ,
,  .
.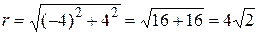 ,
,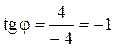 ,
,  .
. , 3π/4).
, 3π/4). ,
,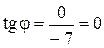 ,
,  .
.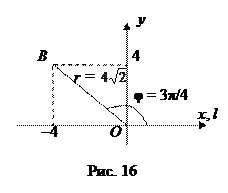
 ,
, 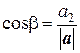 ,
, 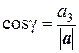 ,
,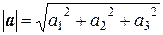 .
.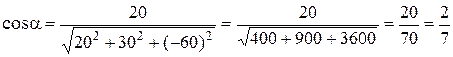 ,
,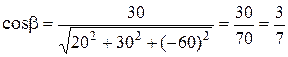 ,
, .
. .
.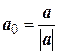 .
.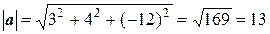 и вектор единичной длины:
и вектор единичной длины: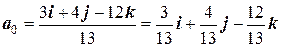 .
.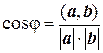 .
.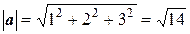 ,
,  , получаем:
, получаем: .
. .
. .
.
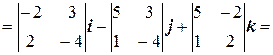

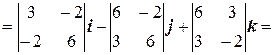
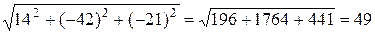 (кв. ед.).
(кв. ед.). и
и 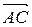 .
.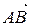 и
и  ]. Таким образом
]. Таким образом |[
|[ 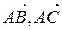 ]|.
]|.
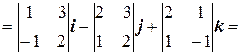 5 i – j – 3 k.
5 i – j – 3 k.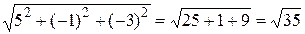 .
. (кв. ед.).
(кв. ед.).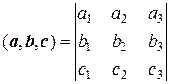 .
. .
. , совпадающих с ребрами пирамиды. Вычитая из координат конца вектора соответствующие координаты начала, получаем
, совпадающих с ребрами пирамиды. Вычитая из координат конца вектора соответствующие координаты начала, получаем = 4 i + j + 3 k.
= 4 i + j + 3 k. .
. .
. (куб. ед.).
(куб. ед.).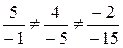 ,
,
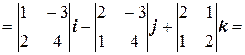

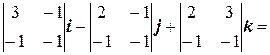
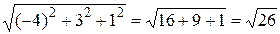 .
.